AVL Tree-
Before you go through this article, make sure that you have gone through the previous article on AVL Trees.
We have discussed-
- AVL trees are self-balancing binary search trees.
- In AVL trees, balancing factor of each node is either 0 or 1 or -1.
In this article, we will discuss AVL Tree Properties.
AVL Tree Properties-
Important properties of AVL tree are-
Property-01:
|
Maximum possible number of nodes in AVL tree of height H
= 2H+1 – 1 |
Example-
Maximum possible number of nodes in AVL tree of height-3
= 23+1 – 1
= 16 – 1
= 15
Thus, in AVL tree of height-3, maximum number of nodes that can be inserted = 15.
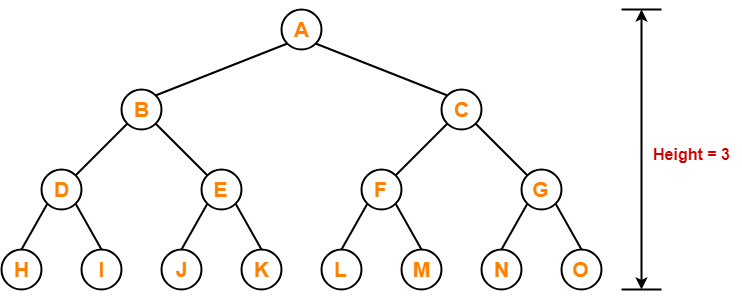
We can not insert more number of nodes in this AVL tree.
Property-02:
|
Minimum number of nodes in AVL Tree of height H is given by a recursive relation-
N(H) = N(H-1) + N(H-2) + 1 |
Base conditions for this recursive relation are-
- N(0) = 1
- N(1) = 2
Example-
Minimum possible number of nodes in AVL tree of height-3 = 7
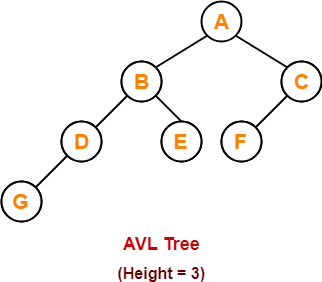
(For explanation, Refer problem-01)
Property-03:
|
Minimum possible height of AVL Tree using N nodes
= ⌊log2N⌋ |
Example-
Minimum possible height of AVL Tree using 8 nodes
= ⌊log28⌋
= ⌊log223⌋
= ⌊3log22⌋
= ⌊3⌋
= 3
Property-04:
|
Maximum height of AVL Tree using N nodes is calculated using recursive relation-
N(H) = N(H-1) + N(H-2) + 1 |
Base conditions for this recursive relation are-
- N(0) = 1
- N(1) = 2
NOTE-
- If there are n nodes in AVL Tree, its maximum height can not exceed 1.44log2n.
- In other words, Worst case height of AVL Tree with n nodes = 1.44log2n.
PRACTICE PROBLEMS BASED ON AVL TREE PROPERTIES-
Problem-01:
Find the minimum number of nodes required to construct AVL Tree of height = 3.
Solution-
We know, minimum number of nodes in AVL tree of height H is given by a recursive relation-
| N(H) = N(H-1) + N(H-2) + 1 |
where N(0) = 1 and N(1) = 2
Step-01:
Substituting H = 3 in the recursive relation, we get-
N(3) = N(3-1) + N(3-2) + 1
N(3) = N(2) + N(1) + 1
N(3) = N(2) + 2 + 1 (Using base condition)
N(3) = N(2) + 3 …………(1)
To solve this recursive relation, we need the value of N(2).
Step-02:
Substituting H = 2 in the recursive relation, we get-
N(2) = N(2-1) + N(2-2) + 1
N(2) = N(1) + N(0) + 1
N(2) = 2 + 1 + 1 (Using base conditions)
∴ N(2) = 4 …………(2)
Step-03:
Using (2) in (1), we get-
N(3) = 4 + 3
∴ N(3) = 7
Thus, minimum number of nodes required to construct AVL tree of height-3 = 7.
Problem-02:
Find the minimum number of nodes required to construct AVL Tree of height = 4.
Solution-
We know, minimum number of nodes in AVL tree of height H is given by a recursive relation-
| N(H) = N(H-1) + N(H-2) + 1 |
where N(0) = 1 and N(1) = 2
Step-01:
Substituting H = 4 in the recursive relation, we get-
N(4) = N(4-1) + N(4-2) + 1
N(4) = N(3) + N(2) + 1 …………(1)
To solve this recursive relation, we need the value of N(2) and N(3).
Step-02:
Substituting H = 2 in the recursive relation, we get-
N(2) = N(2-1) + N(2-2) + 1
N(2) = N(1) + N(0) + 1
N(2) = 2 + 1 + 1 (Using base conditions)
∴ N(2) = 4 …………(2)
Step-03:
Substituting H = 3 in the recursive relation, we get-
N(3) = N(3-1) + N(3-2) + 1
N(3) = N(2) + N(1) + 1
N(3) = 4 + 2 + 1 (Using (2) and base condition)
∴ N(3) = 7 …………(3)
Step-04:
Using (2) and (3) in (1), we get-
N(4) = 7 + 4 + 1
∴ N(4) = 12
Thus, minimum number of nodes required to construct AVL tree of height-4 = 12.
Problem-03:
What is the maximum height of any AVL tree with 10 nodes?
Solution-
For calculating the maximum height of AVL tree with n nodes, we use a recursive relation-
| N(H) = N(H-1) + N(H-2) + 1 |
Step-01:
Substituting H = 2 in the recursive relation, we get-
N(2) = N(2-1) + N(2-2) + 1
N(2) = N(1) + N(0) + 1
N(2) = 2 + 1 + 1 (Using base conditions)
∴ N(2) = 4 …………(1)
So, minimum number of nodes required to construct AVL tree of height-2 = 4.
Step-02:
Substituting H = 3 in the recursive relation, we get-
N(3) = N(3-1) + N(3-2) + 1
N(3) = N(2) + N(1) + 1
N(3) = 4 + 2 + 1 (Using (1) and base condition)
∴ N(3) = 7 …………(2)
So, minimum number of nodes required to construct AVL tree of height-3 = 7.
Step-03:
Substituting H = 4 in the recursive relation, we get-
N(4) = N(4-1) + N(4-2) + 1
N(4) = N(3) + N(2) + 1
N(4) = 7 + 4 + 1 (Using (1) and (2))
∴ N(4) = 12
So, minimum number of nodes required to construct AVL tree of height-4 = 12.
But given number of nodes = 10 which is less than 12.
Thus, maximum height of AVL tree that can be obtained using 10 nodes = 3.
Problem-04:
What is the maximum height of any AVL tree with 77 nodes?
Solution-
For calculating the maximum height of AVL tree with n nodes, we use a recursive relation-
| N(H) = N(H-1) + N(H-2) + 1 |
Step-01:
Substituting H = 2 in the recursive relation, we get-
N(2) = N(2-1) + N(2-2) + 1
N(2) = N(1) + N(0) + 1
N(2) = 2 + 1 + 1 (Using base conditions)
∴ N(2) = 4 …………(1)
So, minimum number of nodes required to construct AVL tree of height-2 = 4.
Step-02:
Substituting H = 3 in the recursive relation, we get-
N(3) = N(3-1) + N(3-2) + 1
N(3) = N(2) + N(1) + 1
N(3) = 4 + 2 + 1 (Using (1) and base condition)
∴ N(3) = 7 …………(2)
So, minimum number of nodes required to construct AVL tree of height-3 = 7.
Step-03:
Substituting H = 4 in the recursive relation, we get-
N(4) = N(4-1) + N(4-2) + 1
N(4) = N(3) + N(2) + 1
N(4) = 7 + 4 + 1 (Using (1) and (2))
∴ N(4) = 12 …………(3)
So, minimum number of nodes required to construct AVL tree of height-4 = 12.
Step-04:
Substituting H = 5 in the recursive relation, we get-
N(5) = N(5-1) + N(5-2) + 1
N(5) = N(4) + N(3) + 1
N(5) = 12 + 7 + 1 (Using (2) and (3))
∴ N(5) = 20 …………(4)
So, minimum number of nodes required to construct AVL tree of height-5 = 20.
Step-05:
Substituting H = 6 in the recursive relation, we get-
N(6) = N(6-1) + N(6-2) + 1
N(6) = N(5) + N(4) + 1
N(6) = 20 + 12 + 1 (Using (3) and (4))
∴ N(6) = 33 …………(5)
So, minimum number of nodes required to construct AVL tree of height-6 = 33.
Step-06:
Substituting H = 7 in the recursive relation, we get-
N(7) = N(7-1) + N(7-2) + 1
N(7) = N(6) + N(5) + 1
N(7) = 33 + 20 + 1 (Using (4) and (5))
∴ N(7) = 54 …………(6)
So, minimum number of nodes required to construct AVL tree of height-7 = 54.
Step-07:
Substituting H = 8 in the recursive relation, we get-
N(8) = N(8-1) + N(8-2) + 1
N(8) = N(7) + N(6) + 1
N(8) = 54 + 33 + 1 (Using (5) and (6))
∴ N(8) = 88 …………(6)
So, minimum number of nodes required to construct AVL tree of height-8 = 88.
But given number of nodes = 77 which is less than 88.
Thus, maximum height of AVL tree that can be obtained using 77 nodes = 7.
Next Article- Insertion in AVL Tree
Get more notes and other study material of Data Structures.
Watch video lectures by visiting our YouTube channel LearnVidFun.

