Paging in OS | Practice Problems | Set-02

Paging in OS-

 

Before you go through this article, make sure that you have gone through the previous articles on Paging in OS.

 

We have discussed-

• Paging is a non-contiguous memory allocation technique.
• Page Table is a table that maps a page number to the frame number containing that page.
• Multilevel Paging is a paging scheme where there exists a hierarchy of page tables.

 

Also Read- Important Formulas of Paging

 

In this article, we will discuss practice problems based on multilevel paging.

 

PRACTICE PROBLEMS BASED ON MULTILEVEL PAGING IN OS-

 

Problem-01:

 

Consider a single level paging scheme. The page size is 4 KB and page table entry size is 4 bytes. The size of page table is 4 KB. Give the division of virtual address space.

 

Solution-

 

Given-

• Page size = 4 KB
• Page table entry size = 4 bytes
• Page table size = 4 KB

 

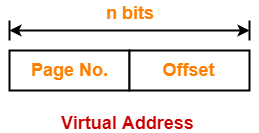
Let the number of bits in virtual address = n bits

 

 

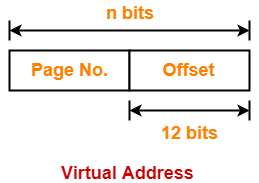
Number of Bits in Page Offset-

 

We have,

Page size

= 4 KB

= 2¹² B

Thus, Number of bits in page offset = 12 bits

 

 

Process Size-

 

Number of bits in virtual address = n bits

Thus,

Process size = 2ⁿ bytes

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 2ⁿ B / 4 KB

= 2ⁿ B / 2¹² B

= 2^n-12 pages

 

Page Table Size-

 

Page table keeps track of the frames storing the pages of process.

Page table size

= Number of entries in page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 2^n-12 x 4 bytes

= 2^n-12+2 bytes

= 2^n-10 bytes

 

But we are given page table size = 4 KB

Thus,

2^n-10 bytes = 4 KB

2^n-10 = 2¹²

n – 10 = 12

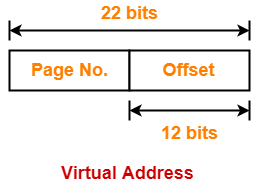
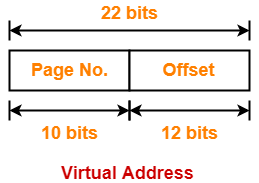
∴ n = 22

Thus, number of bits in virtual address = 22 bits

 

 

Number of Bits Required to Search an Entry in Page Table-

 

Method-01:

 

Number of bits required to search a particular entry in page table

= Number of bits in virtual address – Number of bits in page offset

= 22 bits – 12 bits

= 10 bits

 

Method-02:

 

Number of entries in page table

= Number of pages the process is divided

= 2^n-12

= 2^22-12

= 2¹⁰

Thus, Number of bits required to search a particular entry in page table = 10 bits

 

 

Problem-02:

 

Consider a two level paging scheme. The page size is 4 KB and page table entry size is 4 bytes. The size of outer page table is 4 KB. Give the division of virtual address space.

 

Solution-

 

Given-

• Page size = 4 KB
• Page table entry size = 4 bytes
• Page table size = 4 KB

 

Let the number of bits in virtual address = n bits

 

 

Number of Bits in Page Offset-

 

We have,

Page size

= 4 KB

= 2¹² B

Thus, Number of bits in page offset = 12 bits

 

 

Process Size-

 

Number of bits in virtual address = n bits

Thus,

Process size = 2ⁿ bytes

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 2ⁿ B / 4 KB

= 2ⁿ B / 2¹² B

= 2^n-12 pages

 

Inner Page Table Size-

 

Inner page table keeps track of the frames storing the pages of process.

Inner page table size

= Number of entries in inner page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 2^n-12 x 4 bytes

= 2^n-12+2 bytes

= 2^n-10 bytes

 

Number of Pages of Inner Page Table-

 

Number of pages the inner page table is divided

= Inner page table size / Page size

= 2^n-10 B / 4 KB

= 2^n-10 B / 2¹² B

= 2^n-10-12

= 2^n-22 pages

 

Now, these 2^n-22 pages of inner page table are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Inner Page Table-

 

Number of page table entries in one page of inner page table

= Page size / Page table entry size

= 4 KB / 4 bytes

= 1 K

= 2¹⁰ entries

 

Number of Bits Required to Search an Entry in One Page of Inner Page Table-

 

One page of inner page table contains 2¹⁰ entries.

Thus,

Number of bits required to search a particular entry in one page of inner page table = 10 bits

 

 

Outer Page Table Size-

 

Outer page table is required to keep track of the frames storing the pages of inner page table.

Outer page table size

= Number of entries in outer page table x Page table entry size

= Number of pages the inner page table is divided x Page table entry size

= 2^n-22 x 4 bytes

= 2^n-22+2 bytes

= 2^n-20 bytes

 

But we are given outer page table size = 4 KB

Thus,

2^n-20 bytes = 4 KB

2^n-20 = 2¹²

n – 20 = 12

∴ n = 32

Thus, number of bits in virtual address = 32 bits

 

 

Number of Bits Required to Search an Entry in Outer Page Table-

 

Method-01:

 

Number of bits required to search a particular entry in outer page table

= Number of bits in virtual address – (Number of bits required to search an entry in inner page table + Number of bits in page offset)

= 32 bits – (10 bits + 12 bits)

= 32 bits – 22 bits

= 10 bits

 

Method-02:

 

Number of entries in outer page table

= Number of pages the inner page table is divided

= 2^n-22

= 2^32-22

= 2¹⁰

Thus, Number of bits required to search a particular entry in outer page table = 10 bits

 

 

Problem-03:

 

Consider a three level paging scheme. The page size is 4 KB and page table entry size is 4 bytes. The size of outermost page table is 4 KB. Give the division of virtual address space.

 

Solution-

 

Given-

• Page size = 4 KB
• Page table entry size = 4 bytes
• Page table size = 4 KB

 

Let the number of bits in virtual address = n bits

 

 

Number of Bits in Page Offset-

 

We have,

Page size

= 4 KB

= 2¹² B

Thus, Number of bits in page offset = 12 bits

 

 

Process Size-

 

Number of bits in virtual address = n bits

Thus,

Process size = 2ⁿ bytes

 

Number of Pages of Process-

 

Number of pages the process is divided

= Process size / Page size

= 2ⁿ B / 4 KB

= 2ⁿ B / 2¹² B

= 2^n-12 pages

 

Inner Page Table Size-

 

Inner page table keeps track of the frames storing the pages of process.

Inner page table size

= Number of entries in inner page table x Page table entry size

= Number of pages the process is divided x Page table entry size

= 2^n-12 x 4 bytes

= 2^n-12+2 bytes

= 2^n-10 bytes

 

Number of Pages of Inner Page Table-

 

Number of pages the inner page table is divided

= Inner page table size / Page size

= 2^n-10 B / 4 KB

= 2^n-10 B / 2¹² B

= 2^n-10-12

= 2^n-22 pages

 

Now, these 2^n-22 pages of inner page table are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Inner Page Table-

 

Number of page table entries in one page of inner page table

= Page size / Page table entry size

= 4 KB / 4 bytes

= 1 K

= 2¹⁰ entries

 

Number of Bits Required to Search an Entry in One Page of Inner Page Table-

 

One page of inner page table contains 2¹⁰ entries.

Thus,

Number of bits required to search a particular entry in one page of inner page table = 10 bits

 

 

Outer Page Table-1 Size-

 

Outer page table-1 is required to keep track of the frames storing the pages of inner page table.

Outer page table-1 size

= Number of entries in outer page table-1 x Page table entry size

= Number of pages the inner page table is divided x Page table entry size

= 2^n-22 x 4 bytes

= 2^n-22+2 bytes

= 2^n-20 bytes

 

Number of Pages of Outer Page Table-1

 

Number of pages the outer page table-1 is divided

= Outer page table-1 size / Page size

= 2^n-20 B / 4 KB

= 2^n-20 B / 2¹² B

= 2^n-20-12

= 2^n-32 pages

 

Now, these 2^n-32 pages of outer page table-1 are stored in different frames of the main memory.

 

Number of Page Table Entries in One Page of Outer Page Table-1

 

Number of page table entries in one page of outer page table-1

= Page size / Page table entry size

= 4 KB / 4 bytes

= 1 K

= 2¹⁰ entries

 

Number of Bits Required to Search an Entry in One Page of Outer Page Table-1

 

One page of outer page table-1 contains 2¹⁰ entries.

Thus,

Number of bits required to search a particular entry in one page of outer page table-1 = 10 bits

 

 

Outer Page Table-2 Size-

 

Outer page table-2 is required to keep track of the frames storing the pages of outer page table-1.

Outer page table-2 size

= Number of entries in outer page table-2 x Page table entry size

= Number of pages the outer page table-1 is divided x Page table entry size

= 2^n-32 x 4 bytes

= 2^n-32+2 bytes

= 2^n-30 bytes

 

But we are given outermost page table size = 4 KB

Thus,

2^n-30 bytes = 4 KB

2^n-30 = 2¹²

n – 30 = 12

∴ n = 42

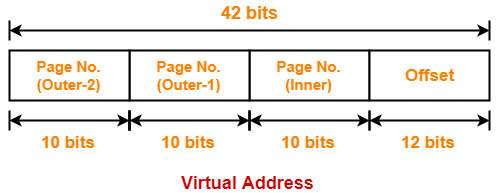
Thus, number of bits in virtual address = 42 bits

 

 

Number of Bits Required to Search an Entry in Outer Page Table-2

 

Method-01:

 

Number of bits required to search a particular entry in outer page table-2

= Number of bits in virtual address – (Number of bits required to search an entry in outer page table-1 + Number of bits required to search an entry in inner page table + Number of bits in page offset)

= 42 bits – (10 bits + 10 bits + 12 bits)

= 42 bits – 32 bits

= 10 bits

 

Method-02:

 

Number of entries in outer page table-2

= Number of pages the outer page table-1 is divided

= 2^n-32

= 2^42-32

= 2¹⁰

Thus, Number of bits required to search a particular entry in outer page table-2 = 10 bits

 

 

Problem-04:

 

Complete the following table-

 

Page Size	Page Table Entry Size	Outermost Page Table Size	Levels of Paging	Virtual Address Space Division
4 KB	4 bytes	256 bytes	1	?
4 KB	4 bytes	256 bytes	2	?
4 KB	4 bytes	256 bytes	3	?

 

Solution-

 

• We have to solve these problems in exactly the same manner as we have solved above.
• So, try yourself.

 

The answers to these problems are-

1. 6 bits, 12 bits
2. 6 bits, 10 bits, 12 bits
3. 6 bits, 10 bits, 10 bits, 12 bits

 

Next Article- Practice Problems On Multilevel Paging Using TLB | Set-03

 

Get more notes and other study material of Operating System.

Watch video lectures by visiting our YouTube channel LearnVidFun.