Parse Tree | Derivations | Automata

Parse Tree-

 

• The process of deriving a string is called as derivation.
• The geometrical representation of a derivation is called as a parse tree or derivation tree.

 

 

1. Leftmost Derivation-

 

• The process of deriving a string by expanding the leftmost non-terminal at each step is called as leftmost derivation.
• The geometrical representation of leftmost derivation is called as a leftmost derivation tree.

 

Example-

 

Consider the following grammar-

S → aB / bA

S → aS / bAA / a

B → bS / aBB / b

(Unambiguous Grammar)

 

Let us consider a string w = aaabbabbba

Now, let us derive the string w using leftmost derivation.

 

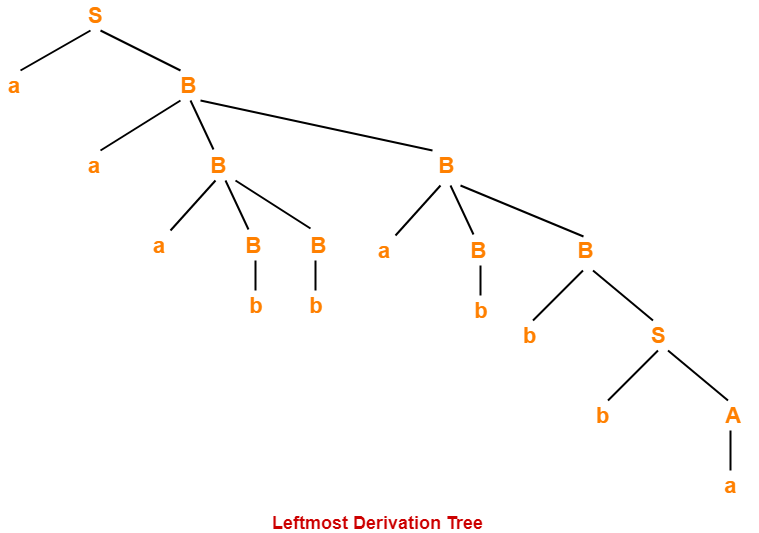
Leftmost Derivation-

 

S   → aB

→  aaBB                   (Using B → aBB)

→ aaaBBB                (Using B → aBB)

→ aaabBB                (Using B → b)

→ aaabbB                (Using B → b)

→ aaabbaBB            (Using B → aBB)

→ aaabbabB            (Using B → b)

→ aaabbabbS          (Using B → bS)

→ aaabbabbbA        (Using S → bA)

→ aaabbabbba         (Using A → a)

 

 

2. Rightmost Derivation-

 

• The process of deriving a string by expanding the rightmost non-terminal at each step is called as rightmost derivation.
• The geometrical representation of rightmost derivation is called as a rightmost derivation tree.

 

Example-

 

Consider the following grammar-

S → aB / bA

S → aS / bAA / a

B → bS / aBB / b

(Unambiguous Grammar)

 

Let us consider a string w = aaabbabbba

Now, let us derive the string w using rightmost derivation.

 

Rightmost Derivation-

 

S   → aB

→  aaBB                    (Using B → aBB)

→ aaBaBB                 (Using B → aBB)

→ aaBaBbS               (Using B → bS)

→ aaBaBbbA             (Using S → bA)

→ aaBaBbba              (Using A → a)

→ aaBabbba              (Using B → b)

→ aaaBBabbba          (Using B → aBB)

→ aaaBbabbba          (Using B → b)

→ aaabbabbba           (Using B → b)

 

 

NOTES For unambiguous grammars, Leftmost derivation and Rightmost derivation represents the same parse tree. For ambiguous grammars, Leftmost derivation and Rightmost derivation represents different parse trees.

 

Here,

• The given grammar was unambiguous.
• That is why, leftmost derivation and rightmost derivation represents the same parse tree.

 

Leftmost Derivation Tree = Rightmost Derivation Tree

 

Also Read- Ambiguous Grammar

 

Properties Of Parse Tree-

 

• Root node of a parse tree is the start symbol of the grammar.
• Each leaf node of a parse tree represents a terminal symbol.
• Each interior node of a parse tree represents a non-terminal symbol.
• Parse tree is independent of the order in which the productions are used during derivations.

 

Yield Of Parse Tree-

 

• Concatenating the leaves of a parse tree from the left produces a string of terminals.
• This string of terminals is called as yield of a parse tree.

 

PRACTICE PROBLEMS BASED ON DERIVATIONS AND PARSE TREE-

 

Problem-01:

 

Consider the grammar-

S → bB / aA

A → b / bS / aAA

B → a / aS / bBB

 

For the string w = bbaababa, find-

1. Leftmost derivation
2. Rightmost derivation
3. Parse Tree

 

Solution-

 

1. Leftmost Derivation-

 

S   → bB

→ bbBB              (Using B → bBB)

→ bbaB              (Using B → a)

→ bbaaS            (Using B → aS)

→ bbaabB          (Using S → bB)

→ bbaabaS        (Using B → aS)

→ bbaababB      (Using S → bB)

→ bbaababa       (Using B → a)

 

2. Rightmost Derivation-

 

S   → bB

→ bbBB                (Using B → bBB)

→ bbBaS              (Using B → aS)

→ bbBabB            (Using S → bB)

→ bbBabaS          (Using B → aS)

→ bbBababB        (Using S → bB)

→ bbBababa        (Using B → a)

→ bbaababa         (Using B → a)

 

3. Parse Tree-

 

 

• Whether we consider the leftmost derivation or rightmost derivation, we get the above parse tree.
• The reason is given grammar is unambiguous.

 

Problem-02:

 

Consider the grammar-

S → A1B

A → 0A / ∈

B → 0B / 1B / ∈

 

For the string w = 00101, find-

1. Leftmost derivation
2. Rightmost derivation
3. Parse Tree

 

Solution-

 

1. Leftmost Derivation-

 

S   → A1B

→ 0A1B              (Using A → 0A)

→ 00A1B            (Using A → 0A)

→ 001B              (Using A → ∈)

→ 0010B            (Using B → 0B)

→ 00101B          (Using B → 1B)

→ 00101             (Using B → ∈)

 

2. Rightmost Derivation-

 

S   → A1B

→ A10B                (Using B → 0B)

→ A101B              (Using B → 1B)

→ A101                (Using B → ∈)

→ 0A101              (Using A → 0A)

→ 00A101            (Using A → 0A)

→ 00101               (Using A → ∈)

 

3. Parse Tree-

 

 

• Whether we consider the leftmost derivation or rightmost derivation, we get the above parse tree.
• The reason is given grammar is unambiguous.

 

To gain better understanding about Derivations and Parse Tree,

Watch this Video Lecture

 

Next Article- Elimination of Left Recursion

 

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.