Introduction to Algorithms By Cormen
This article reviews the book “Introduction to Algorithms” by Thomas H. Cormen.
The article covers-
- Special features of book
- Analysis of Content
- Analysis of Exercises
- Necessary Instructions
- Conclusion
Why Should Be Read?
Special Features of Book-
The special features of this book are-
- It has an in-depth and elaborative explanation which is unmatched by any other book.
- The algorithms are explained followed by their analysis and proofs.
- It provides a detailed insight into the subject.
- The analysis part is covered very well and multiple readings may be needed for some algorithms.
- The exercise questions are pretty good.
- Some GATE questions have been asked directly from its exercises in the previous year exams.
- Data structures are covered equally good.
Analysis of Content-
The following table analyzes sections of the book that are relevant for GATE-
| Chapter No. | GATE Relevant Sections | GATE Topics Covered |
| 1 | 1.1 | Basics of Algorithms |
| 1.2 | ||
| 2 | 2.1 | Insertion Sort |
| 2.2 | ||
| 2.3 | Merge Sort | |
| 3 | All Sections | Asymptotic Notations & Growth of Functions |
| 4 | 4.1 to 4.3 | Divide & Conquer, Solving Recurrences, Master’s Theorem |
| 4.5 | ||
| 6 | All Sections | Heap Sort & Priority Queues |
| 7 | 7.1 | Quick Sort |
| 7.2 | ||
| 7.4 | ||
| 8 | All Sections | Counting Sort, Radix Sort, Bucket Sort |
| 10 | 10.1 | Stacks, Queues & Linked List |
| 10.2 | ||
| 10.4 | ||
| 11 | 11.1 to 11.4 | Hashing, Open Addressing |
| 12 | 12.1 to 12.3 | Binary Trees |
| 15 | 15.1 | Dynamic Programming Algorithms |
| 15.2 | ||
| 15.4 | ||
| 16 | 16.1 to 16.3 | Greedy Algorithms |
| 22 | All Sections | Graph Representations & Traversal Algorithms |
| 23 | All Sections | Minimum Spanning Tree Algorithms
(Prim’s and Kruskal’s) |
| 24 | 24.1 to 24.3 | Bellman Ford & Dijkstra’s Algorithm |
| 25 | 25.2 | Floyd-Warshall Algorithm |
Covering Only These Sections Is Enough
Analysis of Exercises-
The following table analyzes exercises of the book that are relevant for GATE-
| Chapter No. | Question No. |
| 1 | 1.2-2, 1.2-3 |
| 2 | 2.1-1, 2.1-2, 2.2-1, 2.2-2, 2.3-1, 2.3-3, 2.3-5, 2.3-6, 2.3-7, 2.1, 2.4 |
| 3 | 3.1-1, 3.1-2, 3.1-4, 3.2-3, 3.1, 3.3, 3.4 |
| 4 | 4.2-1, 4.2-3, 4.3-1, 4.3-2, 4.3-3, 4.3-6, 4.3-9, 4.4-1, 4.4-2, 4.4-3, 4.4-4, 4.4-5, 4.5-1, 4.5-3, 4.5-4, 4.1, 4.3, 4.5, 4.6 |
| 6 | 6.1-1 to 6.1-7, 6.2-1, 6.2-6, 6.3-1 to 6.3-3, 6.4-1, 6.4-3, 6.5-1, 6.5-7, 6.5-9, 6.2, 6.3 |
| 7 | 7.1-1 to 7.1-4, 7.2-1 to 7.2-3, 7.4-6, 7.4 |
| 8 | 8.2-1, 8.2-2, 8.3-1, 8.3-2, 8.3-4, 8.4-1, 8.4-2, 8.4-3, 8.2, 8.3 |
| 10 | 10.1-1 to 10.1-7, 10.2-2, 10.2-3, 10.2-8, 10.4-1 to 10.4-6, 10.1 |
| 11 | 11.2-1 to 11.2-3, 11.4-1, 11.4-3 |
| 12 | 12.1-1 to 12.1-5, 12.2-1, 12.2-5, 12.2-6 |
| 15 | 15.1-3 to 15.1-5, 15.2-1, 15.2-6, 15.4-1, 15.4-3 |
| 16 | 16.1-2, 16.1-4, 16.2-1, 16.2-2, 16.2-3, 16.2-6, 16.3-3 |
| 22 | 22.1-1, 22.1-2, 22.1-4, 22.1-6, 22.1-7, 22.2-1, 22.2-2, 22.2-4, 22.2-7, 22.2-8, 22.3-5, 22.3-8, 22.3-9, 22.3-11, 22.3-13, 22.4-1, 22.4-3, 22.4-4, 22.5-1, 22.5-4, 22.1 to 22.3 |
| 23 | 23.1-1 to 23.1-11, 23.2-2 to 23.2-5, 23.2, 23.3 |
| 24 | 24.1-1, 24.1-6, 24.2-1, 24.3-1, 24.3-2, 24.3-10 |
| 25 | 25.2-4, 25.2-6, 25.2-8 |
Practicing Only These Exercises Is Enough
Necessary Instructions-
Keep the following instructions in mind while reading the book-
- The book has nearly 1300 pages and all the topics are explained in great detail.
- You need to be pretty selective with what topics you need to read. (Refer above)
- Since GATE does not have subjective questions, so there is no need to cover the proofs.
- However, studying the proofs deepens the knowledge of algorithms.
- Go for studying the proofs only if you have ample time.
You can divide reading the book in three levels-
Level-01:
- Read the algorithm.
- Try to understand how it works and implement on a few examples.
- Implement the algorithm code in some programming language if you have time.
- Prefer C language as it is a part of GATE syllabus.
Level-02:
- Read the analysis part and proof of correctness for that algorithm.
- This part is important as GATE questions focus on the analysis aspect of algorithms.
Level-03:
- Try solving the problems at the end of each chapter.
- The problems are of medium and tough difficulty level and requires thorough knowledge.
Conclusion-
- The book covers all the algorithms in an extensive way focusing equally on the analysis aspect.
- The exercise questions are intuitive and guide the students to cover topics in depth.
- The exercise questions of this book have been asked directly in GATE .
- Most of the questions are at par with the level of questions asked in GATE.
- This book is a must read for every student who wants to learn algorithms.
| THIS BOOK IS MORE THAN ENOUGH FOR GATE EXAM. |
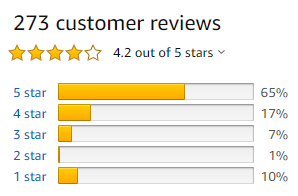
Amazon Rating
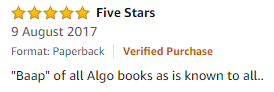
Student’s Reviews-








Other Recommended Books-
Algorithm Design By Kleinberg and Tardos-



