Tag: Decimal to 8 bit Binary

Decimal to Binary Conversion | Base 10 to base 2

Number System

Number System Conversions-

 

Before you go through this article, make sure that you have gone through the previous article on Basics of Number System.

 

In number system,

  • It is very important to have a good knowledge of how to convert numbers from one base to another base.
  • Here, we will learn how to convert any given number from base 10 to base 2.

 

 

Decimal to Binary Conversion-

 

A given number can be converted from base 10 to any other base using division method and multiplication method.

 

Learn how much goods and services should cost from painting a car or reupholstering a car windshield

to hiring wedding planner or a cook at The Pricer.

 

Following two cases are possible-

 

Case-01: For Numbers Carrying No Fractional Part-

 

  • Division Method is used to convert such numbers from base 10 to another base.
  • The division is performed with the required base.

 

Steps To Convert From Base 10 to Base 2-

 

  • Divide the given number (in base 10) with 2 until the result finally left is less than 2.
  • Traverse the remainders from bottom to top to get the required number in base 2.

 

Case-02: For Numbers Carrying A Fractional Part-

 

To convert such numbers from base 10 to another base, real part and fractional part are treated separately.

 

For Real Part-

 

The steps involved in converting the real part from base 10 to another base are same as above.

 

For Fractional Part-

 

  • Multiplication Method is used to convert fractional part from base 10 to another base.
  • The multiplication is performed with the required base.

 

Steps To Convert From Base 10 To Base 2-

 

  • Multiply the given fraction (in base 10) with 2.
  • Write the real part and fractional part of the result so obtained separately.
  • Multiply the fractional part with 2.
  • Write the real part and fractional part of the result so obtained separately.
  • Repeat this procedure until the fractional part remains 0.
  • If fractional part does not terminate to 0, find the result up to as many places as required.

 

Required Number in Base 2

= Series of real part of multiplication results obtained in the above steps from top to bottom

 

Also Read- Conversion to Base 10

 

PRACTICE PROBLEMS BASED ON DECIMAL TO BINARY CONVERSION-

 

Problems-

 

Convert the following numbers from base 10 to base 2-

  1. (18)10
  2. (18.625)10
  3. (172)10
  4. (172.878)10

 

Solution-

 

1. (18)10

 

(18)10 → ( ? )2

 

Using division method, we have-

 

 

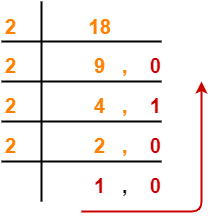
From here, (18)10 = (10010)2

 

2. (18.625)10

 

(18.625)10 → ( ? )2

 

Here, we treat the real part and fractional part separately-

 

For Real Part-

 

  • The real part is (18)10
  • We convert the real part from base 10 to base 2 using division method same as above.

 

So, (18)10 = (10010)2

 

For Fractional Part-

 

  • The fractional part is (0.625)10
  • We convert the fractional part from base 10 to base 2 using multiplication method.

 

Using multiplication method, we have-

 

Real part Fractional Part
0.625 x 2 1 0.25
0.25 x 2 0 0.50
0.50 x 2 1 0

 

Explanation

 

Step-01:

 

  • Multiply 0.625 with 2. Result = 1.25.
  • Write 1 in real part and 0.25 in fractional part.

 

Step-02:

 

  • Multiply 0.25 with 2. Result = 0.50.
  • Write 0 in real part and 0.50 in fractional part.

 

Step-03:

 

  • Multiply 0.50 with 2. Result = 1.0.
  • Write 1 in real part and 0.0 in fractional part.

 

Since fractional part becomes 0, so we stop.

 

  • The fractional part terminates to 0 after 3 iterations.
  • Traverse the real part column from top to bottom to obtain the required number in base 2.

 

From here, (0.625)10 = (0.101)2

 

Combining the results of real part and fractional part, we have-

(18.625)10 = (10010.101)2

 

3. (172)10

 

(172)10 → ( ? )2

 

Using division method, we have-

 

 

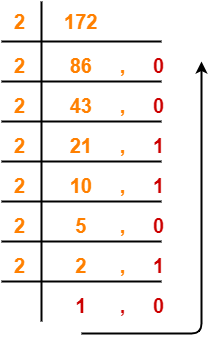
From here, (172)10 = (10101100)2

 

4. (172.878)10

 

(172.878)10 → ( ? )2

 

Here, we treat the real part and fractional part separately-

 

For Real Part-

 

  • The real part is (172)10
  • We convert the real part from base 10 to base 2 using division method same as above.

 

So, (172)10 = (10101100)2

 

For Fractional Part-

 

  • The fractional part is (0.878)10
  • We convert the fractional part from base 10 to base 2 using multiplication method.

 

Using multiplication method, we have-

 

Real part Fractional Part
0.878 x 2 1 0.756
0.756 x 2 1 0.512
0.512 x 2 1 0.024
0.024 x 2 0 0.048

 

  • The fractional part does not terminates to 0 after several iterations.
  • So, let us find the value up to 4 decimal places.
  • Traverse the real part column from top to bottom to obtain the required number in base 2.

 

From here, (0.878)10 = (0.1110)2

 

Combining the results of real part and fractional part, we have-

(172.878)10 = (10101100.1110)2

 

To gain better understanding about Decimal to Binary Conversion,

Watch this Video Lecture

 

Next Article- Decimal to Octal Conversion

 

Get more notes and other study material of Number System.

Watch video lectures by visiting our YouTube channel LearnVidFun.