K-Means Clustering-
- K-Means clustering is an unsupervised iterative clustering technique.
- It partitions the given data set into k predefined distinct clusters.
- A cluster is defined as a collection of data points exhibiting certain similarities.

It partitions the data set such that-
- Each data point belongs to a cluster with the nearest mean.
- Data points belonging to one cluster have high degree of similarity.
- Data points belonging to different clusters have high degree of dissimilarity.
K-Means Clustering Algorithm-
K-Means Clustering Algorithm involves the following steps-
Step-01:
- Choose the number of clusters K.
Step-02:
- Randomly select any K data points as cluster centers.
- Select cluster centers in such a way that they are as farther as possible from each other.
Step-03:
- Calculate the distance between each data point and each cluster center.
- The distance may be calculated either by using given distance function or by using euclidean distance formula.
Step-04:
- Assign each data point to some cluster.
- A data point is assigned to that cluster whose center is nearest to that data point.
Step-05:
- Re-compute the center of newly formed clusters.
- The center of a cluster is computed by taking mean of all the data points contained in that cluster.
Step-06:
Keep repeating the procedure from Step-03 to Step-05 until any of the following stopping criteria is met-
- Center of newly formed clusters do not change
- Data points remain present in the same cluster
- Maximum number of iterations are reached
Advantages-
K-Means Clustering Algorithm offers the following advantages-
Point-01:
It is relatively efficient with time complexity O(nkt) where-
- n = number of instances
- k = number of clusters
- t = number of iterations
Point-02:
- It often terminates at local optimum.
- Techniques such as Simulated Annealing or Genetic Algorithms may be used to find the global optimum.
Disadvantages-
K-Means Clustering Algorithm has the following disadvantages-
- It requires to specify the number of clusters (k) in advance.
- It can not handle noisy data and outliers.
- It is not suitable to identify clusters with non-convex shapes.
PRACTICE PROBLEMS BASED ON K-MEANS CLUSTERING ALGORITHM-
Problem-01:
Cluster the following eight points (with (x, y) representing locations) into three clusters:
A1(2, 10), A2(2, 5), A3(8, 4), A4(5, 8), A5(7, 5), A6(6, 4), A7(1, 2), A8(4, 9)
Initial cluster centers are: A1(2, 10), A4(5, 8) and A7(1, 2).
The distance function between two points a = (x1, y1) and b = (x2, y2) is defined as-
Ρ(a, b) = |x2 – x1| + |y2 – y1|
Use K-Means Algorithm to find the three cluster centers after the second iteration.
Solution-
We follow the above discussed K-Means Clustering Algorithm-
Iteration-01:
- We calculate the distance of each point from each of the center of the three clusters.
- The distance is calculated by using the given distance function.
The following illustration shows the calculation of distance between point A1(2, 10) and each of the center of the three clusters-
Calculating Distance Between A1(2, 10) and C1(2, 10)-
Ρ(A1, C1)
= |x2 – x1| + |y2 – y1|
= |2 – 2| + |10 – 10|
= 0
Calculating Distance Between A1(2, 10) and C2(5, 8)-
Ρ(A1, C2)
= |x2 – x1| + |y2 – y1|
= |5 – 2| + |8 – 10|
= 3 + 2
= 5
Calculating Distance Between A1(2, 10) and C3(1, 2)-
Ρ(A1, C3)
= |x2 – x1| + |y2 – y1|
= |1 – 2| + |2 – 10|
= 1 + 8
= 9
In the similar manner, we calculate the distance of other points from each of the center of the three clusters.
Next,
- We draw a table showing all the results.
- Using the table, we decide which point belongs to which cluster.
- The given point belongs to that cluster whose center is nearest to it.
| Given Points | Distance from center (2, 10) of Cluster-01 | Distance from center (5, 8) of Cluster-02 | Distance from center (1, 2) of Cluster-03 | Point belongs to Cluster |
| A1(2, 10) | 0 | 5 | 9 | C1 |
| A2(2, 5) | 5 | 6 | 4 | C3 |
| A3(8, 4) | 12 | 7 | 9 | C2 |
| A4(5, 8) | 5 | 0 | 10 | C2 |
| A5(7, 5) | 10 | 5 | 9 | C2 |
| A6(6, 4) | 10 | 5 | 7 | C2 |
| A7(1, 2) | 9 | 10 | 0 | C3 |
| A8(4, 9) | 3 | 2 | 10 | C2 |
From here, New clusters are-
Cluster-01:
First cluster contains points-
- A1(2, 10)
Cluster-02:
Second cluster contains points-
- A3(8, 4)
- A4(5, 8)
- A5(7, 5)
- A6(6, 4)
- A8(4, 9)
Cluster-03:
Third cluster contains points-
- A2(2, 5)
- A7(1, 2)
Now,
- We re-compute the new cluster clusters.
- The new cluster center is computed by taking mean of all the points contained in that cluster.
For Cluster-01:
- We have only one point A1(2, 10) in Cluster-01.
- So, cluster center remains the same.
For Cluster-02:
Center of Cluster-02
= ((8 + 5 + 7 + 6 + 4)/5, (4 + 8 + 5 + 4 + 9)/5)
= (6, 6)
For Cluster-03:
Center of Cluster-03
= ((2 + 1)/2, (5 + 2)/2)
= (1.5, 3.5)
This is completion of Iteration-01.
Iteration-02:
- We calculate the distance of each point from each of the center of the three clusters.
- The distance is calculated by using the given distance function.
The following illustration shows the calculation of distance between point A1(2, 10) and each of the center of the three clusters-
Calculating Distance Between A1(2, 10) and C1(2, 10)-
Ρ(A1, C1)
= |x2 – x1| + |y2 – y1|
= |2 – 2| + |10 – 10|
= 0
Calculating Distance Between A1(2, 10) and C2(6, 6)-
Ρ(A1, C2)
= |x2 – x1| + |y2 – y1|
= |6 – 2| + |6 – 10|
= 4 + 4
= 8
Calculating Distance Between A1(2, 10) and C3(1.5, 3.5)-
Ρ(A1, C3)
= |x2 – x1| + |y2 – y1|
= |1.5 – 2| + |3.5 – 10|
= 0.5 + 6.5
= 7
In the similar manner, we calculate the distance of other points from each of the center of the three clusters.
Next,
- We draw a table showing all the results.
- Using the table, we decide which point belongs to which cluster.
- The given point belongs to that cluster whose center is nearest to it.
| Given Points | Distance from center (2, 10) of Cluster-01 | Distance from center (6, 6) of Cluster-02 | Distance from center (1.5, 3.5) of Cluster-03 | Point belongs to Cluster |
| A1(2, 10) | 0 | 8 | 7 | C1 |
| A2(2, 5) | 5 | 5 | 2 | C3 |
| A3(8, 4) | 12 | 4 | 7 | C2 |
| A4(5, 8) | 5 | 3 | 8 | C2 |
| A5(7, 5) | 10 | 2 | 7 | C2 |
| A6(6, 4) | 10 | 2 | 5 | C2 |
| A7(1, 2) | 9 | 9 | 2 | C3 |
| A8(4, 9) | 3 | 5 | 8 | C1 |
From here, New clusters are-
Cluster-01:
First cluster contains points-
- A1(2, 10)
- A8(4, 9)
Cluster-02:
Second cluster contains points-
- A3(8, 4)
- A4(5, 8)
- A5(7, 5)
- A6(6, 4)
Cluster-03:
Third cluster contains points-
- A2(2, 5)
- A7(1, 2)
Now,
- We re-compute the new cluster clusters.
- The new cluster center is computed by taking mean of all the points contained in that cluster.
For Cluster-01:
Center of Cluster-01
= ((2 + 4)/2, (10 + 9)/2)
= (3, 9.5)
For Cluster-02:
Center of Cluster-02
= ((8 + 5 + 7 + 6)/4, (4 + 8 + 5 + 4)/4)
= (6.5, 5.25)
For Cluster-03:
Center of Cluster-03
= ((2 + 1)/2, (5 + 2)/2)
= (1.5, 3.5)
This is completion of Iteration-02.
After second iteration, the center of the three clusters are-
- C1(3, 9.5)
- C2(6.5, 5.25)
- C3(1.5, 3.5)
Problem-02:
Use K-Means Algorithm to create two clusters-
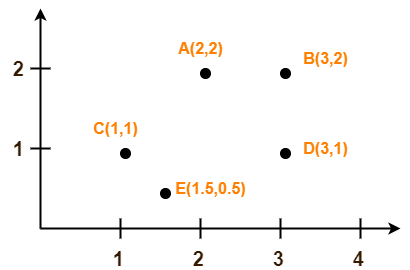
Solution-
We follow the above discussed K-Means Clustering Algorithm.
Assume A(2, 2) and C(1, 1) are centers of the two clusters.
Iteration-01:
- We calculate the distance of each point from each of the center of the two clusters.
- The distance is calculated by using the euclidean distance formula.
The following illustration shows the calculation of distance between point A(2, 2) and each of the center of the two clusters-
Calculating Distance Between A(2, 2) and C1(2, 2)-
Ρ(A, C1)
= sqrt [ (x2 – x1)2 + (y2 – y1)2 ]
= sqrt [ (2 – 2)2 + (2 – 2)2 ]
= sqrt [ 0 + 0 ]
= 0
Calculating Distance Between A(2, 2) and C2(1, 1)-
Ρ(A, C2)
= sqrt [ (x2 – x1)2 + (y2 – y1)2 ]
= sqrt [ (1 – 2)2 + (1 – 2)2 ]
= sqrt [ 1 + 1 ]
= sqrt [ 2 ]
= 1.41
In the similar manner, we calculate the distance of other points from each of the center of the two clusters.
Next,
- We draw a table showing all the results.
- Using the table, we decide which point belongs to which cluster.
- The given point belongs to that cluster whose center is nearest to it.
| Given Points | Distance from center (2, 2) of Cluster-01 | Distance from center (1, 1) of Cluster-02 | Point belongs to Cluster |
| A(2, 2) | 0 | 1.41 | C1 |
| B(3, 2) | 1 | 2.24 | C1 |
| C(1, 1) | 1.41 | 0 | C2 |
| D(3, 1) | 1.41 | 2 | C1 |
| E(1.5, 0.5) | 1.58 | 0.71 | C2 |
From here, New clusters are-
Cluster-01:
First cluster contains points-
- A(2, 2)
- B(3, 2)
- E(1.5, 0.5)
- D(3, 1)
Cluster-02:
Second cluster contains points-
- C(1, 1)
- E(1.5, 0.5)
Now,
- We re-compute the new cluster clusters.
- The new cluster center is computed by taking mean of all the points contained in that cluster.
For Cluster-01:
Center of Cluster-01
= ((2 + 3 + 3)/3, (2 + 2 + 1)/3)
= (2.67, 1.67)
For Cluster-02:
Center of Cluster-02
= ((1 + 1.5)/2, (1 + 0.5)/2)
= (1.25, 0.75)
This is completion of Iteration-01.
Next, we go to iteration-02, iteration-03 and so on until the centers do not change anymore.
To gain better understanding about K-Means Clustering Algorithm,
Next Article- Principal Component Analysis
Get more notes and other study material of Pattern Recognition.
Watch video lectures by visiting our YouTube channel LearnVidFun.