Minimization Of Boolean Expressions-
There are following two methods of minimizing or reducing the boolean expressions-

- By using laws of Boolean Algebra
- By using Karnaugh Maps also called as K Maps
In this article, we will discuss about Karnaugh Maps or K Maps.
Karnaugh Map-
| The Karnaugh Map also called as K Map is a graphical representation
that provides a systematic method for simplifying the boolean expressions. |
For a boolean expression consisting of n-variables, number of cells required in K Map = 2n cells.
Two Variable K Map-
- Two variable K Map is drawn for a boolean expression consisting of two variables.
- The number of cells present in two variable K Map = 22 = 4 cells.
- So, for a boolean function consisting of two variables, we draw a 2 x 2 K Map.
Two variable K Map may be represented as-
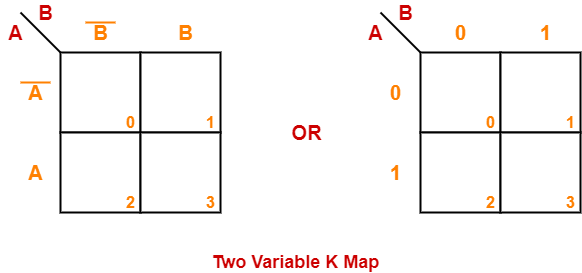
Here, A and B are the two variables of the given boolean function.
Three Variable K Map-
- Three variable K Map is drawn for a boolean expression consisting of three variables.
- The number of cells present in three variable K Map = 23 = 8 cells.
- So, for a boolean function consisting of three variables, we draw a 2 x 4 K Map.
Three variable K Map may be represented as-
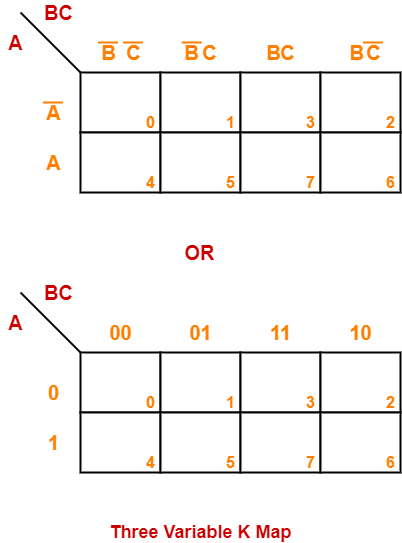
Here, A, B and C are the three variables of the given boolean function.
Four Variable K Map-
- Four variable K Map is drawn for a boolean expression consisting of four variables.
- The number of cells present in four variable K Map = 24 = 16 cells.
- So, for a boolean function consisting of four variables, we draw a 4 x 4 K Map.
Four variable K Map may be represented as-
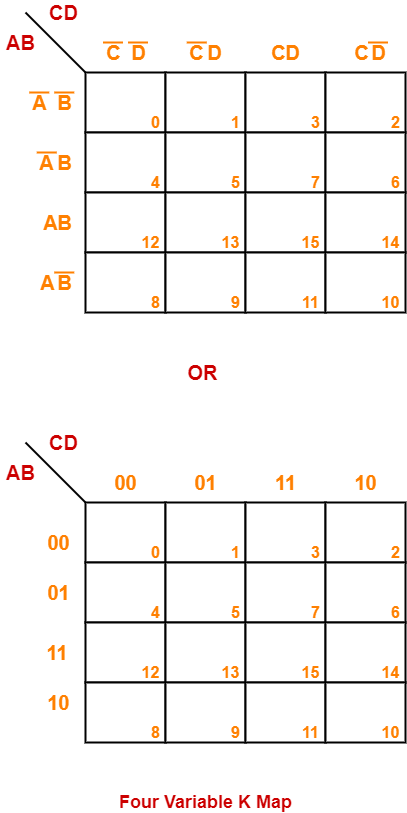
Here, A, B, C and D are the four variables of the given boolean function.
Karnaugh Map Simplification Rules-
To minimize the given boolean function,
- We draw a K Map according to the number of variables it contains.
- We fill the K Map with 0’s and 1’s according to its function.
- Then, we minimize the function in accordance with the following rules.
Rule-01:
- We can either group 0’s with 0’s or 1’s with 1’s but we can not group 0’s and 1’s together.
- X representing don’t care can be grouped with 0’s as well as 1’s.
NOTEThere is no need of separately grouping X’s i.e. they can be ignored if all 0’s and 1’s are already grouped. |
Rule-02:
- Groups may overlap each other.
Rule-03:
- We can only create a group whose number of cells can be represented in the power of 2.
- In other words, a group can only contain 2n i.e. 1, 2, 4, 8, 16 and so on number of cells.
Example-
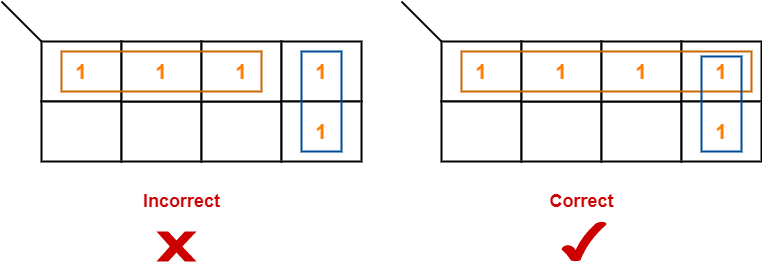
Rule-04:
- Groups can be only either horizontal or vertical.
- We can not create groups of diagonal or any other shape.
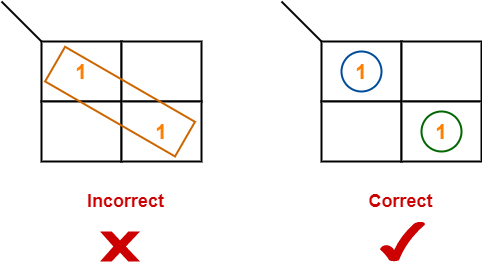
Rule-05:
- Each group should be as large as possible.
Example-
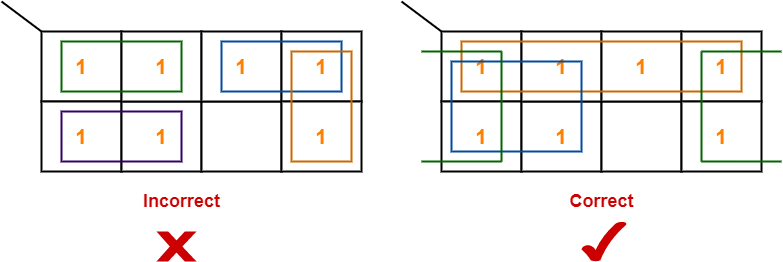
Rule-06:
- Opposite grouping and corner grouping are allowed.
- The example of opposite grouping is shown illustrated in Rule-05.
- The example of corner grouping is shown below.
Example-
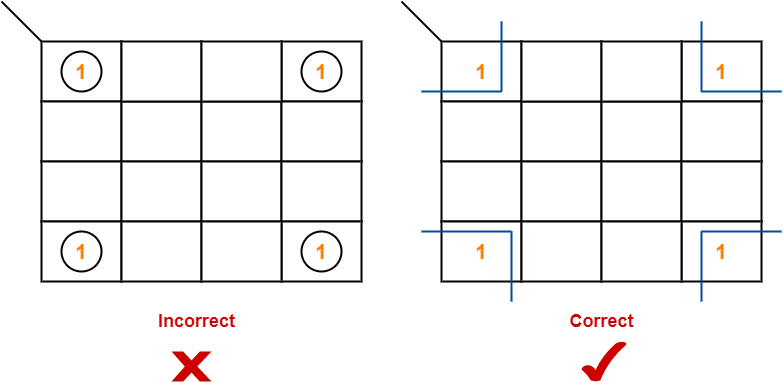
Rule-07:
- There should be as few groups as possible.
PROBLEMS BASED ON KARNAUGH MAP-
Problem-01:
Minimize the following boolean function-
F(A, B, C, D) = Σm(0, 1, 2, 5, 7, 8, 9, 10, 13, 15)
Solution-
- Since the given boolean expression has 4 variables, so we draw a 4 x 4 K Map.
- We fill the cells of K Map in accordance with the given boolean function.
- Then, we form the groups in accordance with the above rules.
Then, we have-
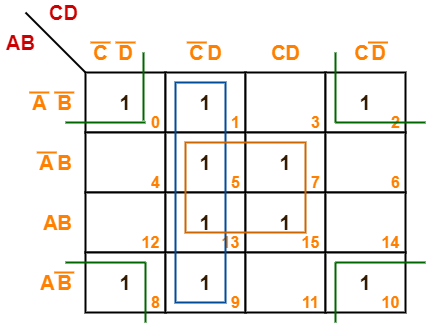
Now,
F(A, B, C, D)
= (A’B + AB)(C’D + CD) + (A’B’ + A’B + AB + AB’)C’D + (A’B’ + AB’)(C’D’ + CD’)
= BD + C’D + B’D’
Thus, minimized boolean expression is-
F(A, B, C, D) = BD + C’D + B’D’
Problem-02:
Minimize the following boolean function-
F(A, B, C, D) = Σm(0, 1, 3, 5, 7, 8, 9, 11, 13, 15)
Solution-
- Since the given boolean expression has 4 variables, so we draw a 4 x 4 K Map.
- We fill the cells of K Map in accordance with the given boolean function.
- Then, we form the groups in accordance with the above rules.
Then, we have-
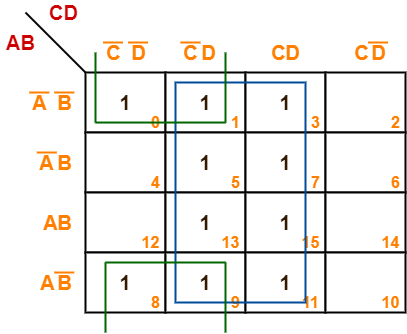
Now,
F(A, B, C, D)
= (A’B’ + A’B + AB + AB’)(C’D + CD) + (A’B’ + AB’)(C’D’ + C’D)
= D + B’C’
Thus, minimized boolean expression is-
F(A, B, C, D) = B’C’ + D
Problem-03:
Minimize the following boolean function-
F(A, B, C, D) = Σm(1, 3, 4, 6, 8, 9, 11, 13, 15) + Σd(0, 2, 14)
Solution-
- Since the given boolean expression has 4 variables, so we draw a 4 x 4 K Map.
- We fill the cells of K Map in accordance with the given boolean function.
- Then, we form the groups in accordance with the above rules.
Then, we have-
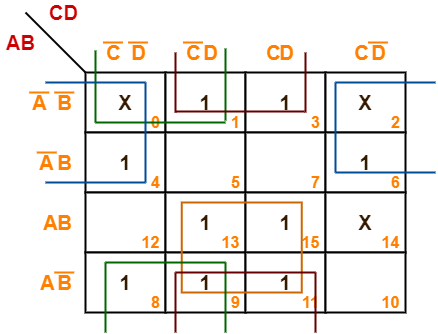
Now,
F(A, B, C, D)
= (AB + AB’)(C’D + CD) + (A’B’ + AB’)(C’D + CD) + (A’B’ + AB’)(C’D’ + C’D) + (A’B’ + A’B)(C’D’ + CD’)
= AD + B’D + B’C’ + A’D’
Thus, minimized boolean expression is-
F(A, B, C, D) = AD + B’D + B’C’ + A’D’
Problem-04:
Minimize the following boolean function-
F(A, B, C) = Σm(0, 1, 6, 7) + Σd(3, 5)
Solution-
- Since the given boolean expression has 3 variables, so we draw a 2 x 4 K Map.
- We fill the cells of K Map in accordance with the given boolean function.
- Then, we form the groups in accordance with the above rules.
Then, we have-
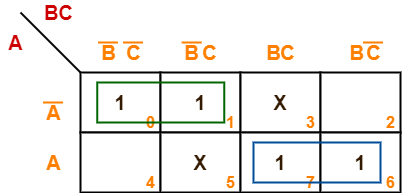
Now,
F(A, B, C)
= A'(B’C’ + B’C) + A(BC + BC’)
= A’B’ + AB
Thus, minimized boolean expression is-
F(A, B, C) = AB + A’B’
NOTE-
- It may be noted that there is no need of considering the quad group.
- This is because even if we consider that group, we will have to consider the other two duets.
- So, there is no use of considering that quad group.
Problem-05:
Minimize the following boolean function-
F(A, B, C) = Σm(1, 2, 5, 7) + Σd(0, 4, 6)
Solution-
- Since the given boolean expression has 3 variables, so we draw a 2 x 4 K Map.
- We fill the cells of K Map in accordance with the given boolean function.
- Then, we form the groups in accordance with the above rules.
Then, we have-
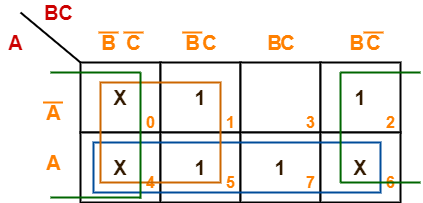
Now,
F(A, B, C)
= (A + A’)(B’C’ + B’C) + A(B’C’ + B’C + BC + BC’) + (A + A’)(B’C’ + BC’)
= B’ + A + C’
Thus, minimized boolean expression is-
F(A, B, C) = A + B’ + C’
Problem-06:
Minimize the following boolean function-
F(A, B, C) = Σm(0, 1, 6, 7) + Σd(3, 4, 5)
Solution-
- Since the given boolean expression has 3 variables, so we draw a 2 x 4 K Map.
- We fill the cells of K Map in accordance with the given boolean function.
- Then, we form the groups in accordance with the above rules.
Then, we have-
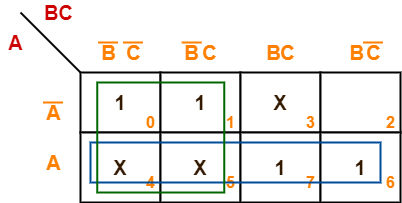
Now,
F(A, B, C)
= (A + A’)(B’C’ + B’C) + A(B’C’ + B’C + BC + BC’)
= B’ + A
Thus, minimized boolean expression is-
F(A, B, C) = A + B’
Problem-07:
Minimize the following boolean function-
F(A, B, C, D) = Σm(0, 2, 8, 10, 14) + Σd(5, 15)
Solution-
- Since the given boolean expression has 4 variables, so we draw a 4 x 4 K Map.
- We fill the cells of K Map in accordance with the given boolean function.
- Then, we form the groups in accordance with the above rules.
Then, we have-
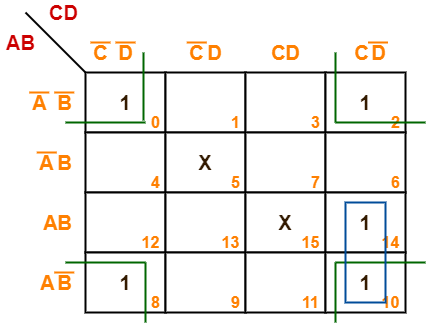
Now,
F(A, B, C, D)
= (AB + AB’)CD’ + (A’B’ + AB’)(C’D’ + CD’)
= ACD’ + B’D’
Thus, minimized boolean expression is-
F(A, B, C, D) = ACD’ + B’D’
Problem-08:
Minimize the following boolean function-
F(A, B, C, D) = Σm(3, 4, 5, 7, 9, 13, 14, 15)
Solution-
- Since the given boolean expression has 4 variables, so we draw a 4 x 4 K Map.
- We fill the cells of K Map in accordance with the given boolean function.
- Then, we form the groups in accordance with the above rules.
Then, we have-
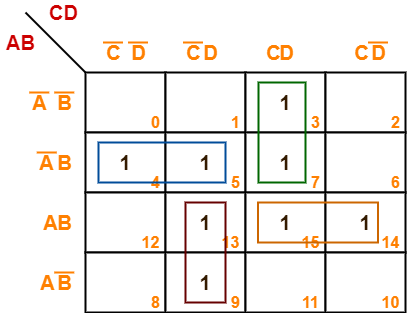
Now,
F(A, B, C, D)
= A’B(C’D’ + C’D) + (A’B’ + A’B)(CD) + (AB + AB’)(C’D) + AB(CD + CD’)
= A’BC’ + A’CD + AC’D + ABC
Thus, minimized boolean expression is-
F(A, B, C, D) = A’BC’ + A’CD + AC’D + ABC
It is important to note that we are not considering the quad group because we have to consider the duets anyhow.
Problem-09:
Consider the following boolean function-
F(W, X, Y, Z) = Σm(1, 3, 4, 6, 9, 11, 12, 14)
This function is independent ________ number of variables. Fill in the blank.
Solution-
- Since the given boolean expression has 4 variables, so we draw a 4 x 4 K Map.
- We fill the cells of K Map in accordance with the given boolean function.
- Then, we form the groups in accordance with the above rules.
Then, we have-
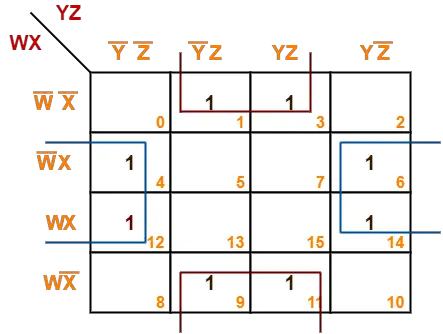
Now,
F(W, X, Y, Z)
= (W’X + WX)(Y’Z’ + YZ’) + (W’X’ + WX’)(Y’Z + YZ)
= XZ’ + X’Z
= X ⊕ Z
Thus, minimized boolean expression is-
F(W, X, Y, Z) = X ⊕ Z
Clearly, the given boolean function depends on only two variables X and Z.
Hence, it is independent of other two variables W and Y.
Next Article- Neutral Functions
Get more notes and other study material of Digital Design.
Watch video lectures by visiting our YouTube channel LearnVidFun.