Tag: CRC Algorithm

Cyclic Redundancy Check | CRC | Example

Computer Networks

Error Detection in Computer Networks-

 

Error detection is a technique that is used to check if any error occurred in the data during the transmission.

 

Some popular error detection methods are-

 

 

  1. Single Parity Check
  2. Cyclic Redundancy Check (CRC)
  3. Checksum

 

In this article, we will discuss about Cyclic Redundancy Check (CRC).

 

Cyclic Redundancy Check-

 

  • Cyclic Redundancy Check (CRC) is an error detection method.
  • It is based on binary division.

 

CRC Generator-

 

  • CRC generator is an algebraic polynomial represented as a bit pattern.
  • Bit pattern is obtained from the CRC generator using the following rule-

 

The power of each term gives the position of the bit and the coefficient gives the value of the bit.

 

Example-

 

Consider the CRC generator is x7 + x6 + x4 + x3 + x + 1.

The corresponding binary pattern is obtained as-

 

 

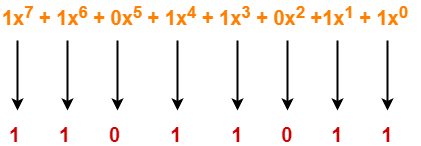
Thus, for the given CRC generator, the corresponding binary pattern is 11011011.

 

Properties Of CRC Generator-

 

The algebraic polynomial chosen as a CRC generator should have at least the following properties-

 

Rule-01:

 

  • It should not be divisible by x.
  • This condition guarantees that all the burst errors of length equal to the length of polynomial are detected.

 

Rule-02:

 

  • It should be divisible by x+1.
  • This condition guarantees that all the burst errors affecting an odd number of bits are detected.

 

Important Notes-

 

If the CRC generator is chosen according to the above rules, then-

  • CRC can detect all single-bit errors
  • CRC can detect all double-bit errors provided the divisor contains at least three logic 1’s.
  • CRC can detect any odd number of errors provided the divisor is a factor of x+1.
  • CRC can detect all burst error of length less than the degree of the polynomial.
  • CRC can detect most of the larger burst errors with a high probability.

 

Steps Involved-

 

Error detection using CRC technique involves the following steps-

 

Step-01: Calculation Of CRC At Sender Side-

 

At sender side,

  • A string of n 0’s is appended to the data unit to be transmitted.
  • Here, n is one less than the number of bits in CRC generator.
  • Binary division is performed of the resultant string with the CRC generator.
  • After division, the remainder so obtained is called as CRC.
  • It may be noted that CRC also consists of n bits.

 

Step-02: Appending CRC To Data Unit-

 

At sender side,

  • The CRC is obtained after the binary division.
  • The string of n 0’s appended to the data unit earlier is replaced by the CRC remainder.

 

Step-03: Transmission To Receiver-

 

  • The newly formed code word (Original data + CRC) is transmitted to the receiver.

 

Step-04: Checking at Receiver Side-

 

At receiver side,

  • The transmitted code word is received.
  • The received code word is divided with the same CRC generator.
  • On division, the remainder so obtained is checked.

 

The following two cases are possible-

 

Case-01: Remainder = 0

 

If the remainder is zero,

  • Receiver assumes that no error occurred in the data during the transmission.
  • Receiver accepts the data.

 

Case-02: Remainder ≠ 0

 

If the remainder is non-zero,

  • Receiver assumes that some error occurred in the data during the transmission.
  • Receiver rejects the data and asks the sender for retransmission.

 

Also Read- Parity Check

 

PRACTICE PROBLEMS BASED ON CYCLIC REDUNDANCY CHECK (CRC)-

 

Problem-01:

 

A bit stream 1101011011 is transmitted using the standard CRC method. The generator polynomial is x4+x+1. What is the actual bit string transmitted?

 

Solution-

 

  • The generator polynomial G(x) = x4 + x + 1 is encoded as 10011.
  • Clearly, the generator polynomial consists of 5 bits.
  • So, a string of 4 zeroes is appended to the bit stream to be transmitted.
  • The resulting bit stream is 11010110110000.

 

Now, the binary division is performed as-

 

 

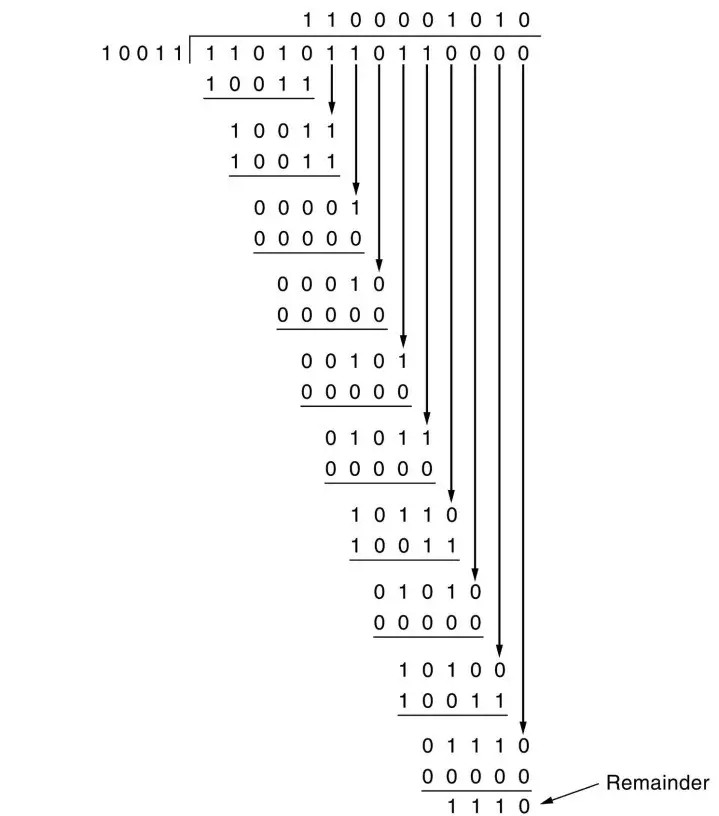
From here, CRC = 1110.

Now,

  • The code word to be transmitted is obtained by replacing the last 4 zeroes of 11010110110000 with the CRC.
  • Thus, the code word transmitted to the receiver = 11010110111110.

 

Problem-02:

 

A bit stream 10011101 is transmitted using the standard CRC method. The generator polynomial is x3+1.

  1. What is the actual bit string transmitted?
  2. Suppose the third bit from the left is inverted during transmission. How will receiver detect this error?

 

Solution-

 

Part-01:

 

  • The generator polynomial G(x) = x3 + 1 is encoded as 1001.
  • Clearly, the generator polynomial consists of 4 bits.
  • So, a string of 3 zeroes is appended to the bit stream to be transmitted.
  • The resulting bit stream is 10011101000.

 

Now, the binary division is performed as-

 

 

From here, CRC = 100.

Now,

  • The code word to be transmitted is obtained by replacing the last 3 zeroes of 10011101000 with the CRC.
  • Thus, the code word transmitted to the receiver = 10011101100.

 

Part-02:

 

According to the question,

  • Third bit from the left gets inverted during transmission.
  • So, the bit stream received by the receiver = 10111101100.

 

Now,

  • Receiver receives the bit stream = 10111101100.
  • Receiver performs the binary division with the same generator polynomial as-

 

 

From here,

  • The remainder obtained on division is a non-zero value.
  • This indicates to the receiver that an error occurred in the data during the transmission.
  • Therefore, receiver rejects the data and asks the sender for retransmission.

 

To watch video solution, click here.

 

To gain better understanding about Cyclic Redundancy Check,

Watch this Video Lecture

 

Next Article- Checksum

 

Get more notes and other study material of Computer Networks.

Watch video lectures by visiting our YouTube channel LearnVidFun.