Cyclomatic Complexity-
Cyclomatic Complexity may be defined as-
- It is a software metric that measures the logical complexity of the program code.
- It counts the number of decisions in the given program code.
- It measures the number of linearly independent paths through the program code.
Cyclomatic complexity indicates several information about the program code-
| Cyclomatic Complexity | Meaning |
| 1 – 10 |
|
| 10 – 20 |
|
| 20 – 40 |
|
| > 40 |
|
Importance of Cyclomatic Complexity-
- It helps in determining the software quality.
- It is an important indicator of program code’s readability, maintainability and portability.
- It helps the developers and testers to determine independent path executions.
- It helps to focus more on the uncovered paths.
- It evaluates the risk associated with the application or program.
- It provides assurance to the developers that all the paths have been tested at least once.
Properties of Cyclomatic Complexity-
- It is the maximum number of independent paths through the program code.
- It depends only on the number of decisions in the program code.
- Insertion or deletion of functional statements from the code does not affect its cyclomatic complexity.
- It is always greater than or equal to 1.
Calculating Cyclomatic Complexity-
Cyclomatic complexity is calculated using the control flow representation of the program code.
In control flow representation of the program code,
- Nodes represent parts of the code having no branches.
- Edges represent possible control flow transfers during program execution
There are 3 commonly used methods for calculating the cyclomatic complexity-
Method-01:
Cyclomatic Complexity = Total number of closed regions in the control flow graph + 1
Method-02:
Cyclomatic Complexity = E – N + 2
Here-
- E = Total number of edges in the control flow graph
- N = Total number of nodes in the control flow graph
Method-03:
Cyclomatic Complexity = P + 1
Here,
P = Total number of predicate nodes contained in the control flow graph
Note-
- Predicate nodes are the conditional nodes.
- They give rise to two branches in the control flow graph.
PRACTICE PROBLEMS BASED ON CYCLOMATIC COMPLEXITY-
Problem-01:
Calculate cyclomatic complexity for the given code-
IF A = 354
THEN IF B > C
THEN A = B
ELSE A = C
END IF
END IF
PRINT A
Solution-
We draw the following control flow graph for the given code-
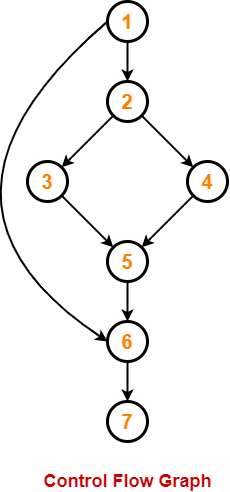
Using the above control flow graph, the cyclomatic complexity may be calculated as-
Method-01:
Cyclomatic Complexity
= Total number of closed regions in the control flow graph + 1
= 2 + 1
= 3
Method-02:
Cyclomatic Complexity
= E – N + 2
= 8 – 7 + 2
= 3
Method-03:
Cyclomatic Complexity
= P + 1
= 2 + 1
= 3
Problem-02:
Calculate cyclomatic complexity for the given code-
{ int i, j, k;
for (i=0 ; i<=N ; i++)
p[i] = 1;
for (i=2 ; i<=N ; i++)
{
k = p[i]; j=1;
while (a[p[j-1]] > a[k] {
p[j] = p[j-1];
j--;
}
p[j]=k;
}
Solution-
We draw the following control flow graph for the given code-
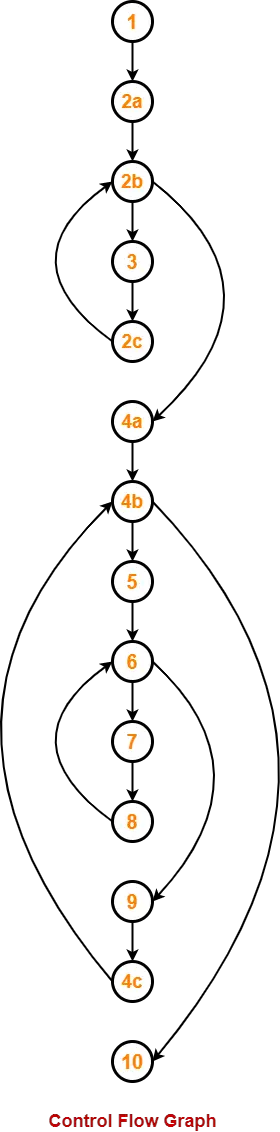
Using the above control flow graph, the cyclomatic complexity may be calculated as-
Method-01:
Cyclomatic Complexity
= Total number of closed regions in the control flow graph + 1
= 3 + 1
= 4
Method-02:
Cyclomatic Complexity
= E – N + 2
= 16 – 14 + 2
= 4
Method-03:
Cyclomatic Complexity
= P + 1
= 3 + 1
= 4
Problem-03:
Calculate cyclomatic complexity for the given code-
begin int x, y, power;
float z;
input(x, y);
if(y<0)
power = -y;
else power = y;
z=1;
while(power!=0)
{ z=z*x;
power=power-1;
} if(y<0)
z=1/z;
output(z);
end
Solution-
We draw the following control flow graph for the given code-
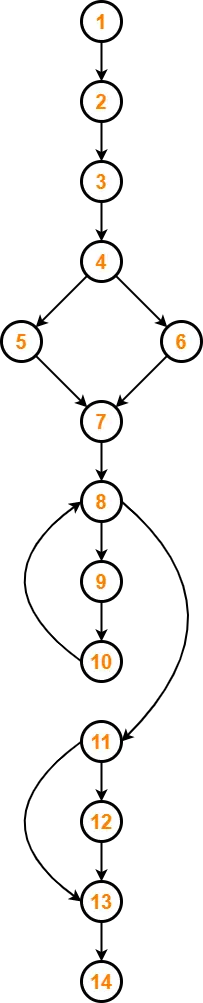
Using the above control flow graph, the cyclomatic complexity may be calculated as-
Method-01:
Cyclomatic Complexity
= Total number of closed regions in the control flow graph + 1
= 3 + 1
= 4
Method-02:
Cyclomatic Complexity
= E – N + 2
= 16 – 14 + 2
= 4
Method-03:
Cyclomatic Complexity
= P + 1
= 3 + 1
= 4
To gain better understanding about Cyclomatic Complexity,
Next Article- Cause Effect Graph Technique
Get more notes and other study material of Software Engineering.
Watch video lectures by visiting our YouTube channel LearnVidFun.