Routing Algorithms-
- Routing algorithms are meant for determining the routing of packets in a node.
- Routing algorithms are classified as-
- Static Routing Algorithms
- Dynamic Routing Algorithms
In this article, we will discuss about distance vector routing.
Distance Vector Routing Algorithm-
| Distance Vector Routing is a dynamic routing algorithm. |
It works in the following steps-
Step-01:
Each router prepares its routing table. By their local knowledge. each router knows about-
- All the routers present in the network
- Distance to its neighboring routers
Step-02:
- Each router exchanges its distance vector with its neighboring routers.
- Each router prepares a new routing table using the distance vectors it has obtained from its neighbors.
- This step is repeated for (n-2) times if there are n routers in the network.
- After this, routing tables converge / become stable.
Distance Vector Routing Example-
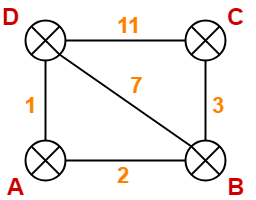
Consider-
- There is a network consisting of 4 routers.
- The weights are mentioned on the edges.
- Weights could be distances or costs or delays.
Step-01:
Each router prepares its routing table using its local knowledge.
Routing table prepared by each router is shown below-
At Router A-
| Destination | Distance | Next Hop |
| A | 0 | A |
| B | 2 | B |
| C | ∞ | – |
| D | 1 | D |
At Router B-
| Destination | Distance | Next Hop |
| A | 2 | A |
| B | 0 | B |
| C | 3 | C |
| D | 7 | D |
At Router C-
| Destination | Distance | Next Hop |
| A | ∞ | – |
| B | 3 | B |
| C | 0 | C |
| D | 11 | D |
At Router D-
| Destination | Distance | Next Hop |
| A | 1 | A |
| B | 7 | B |
| C | 11 | C |
| D | 0 | D |
Step-02:
- Each router exchanges its distance vector obtained in Step-01 with its neighbors.
- After exchanging the distance vectors, each router prepares a new routing table.
This is shown below-
At Router A-
- Router A receives distance vectors from its neighbors B and D.
- Router A prepares a new routing table as-
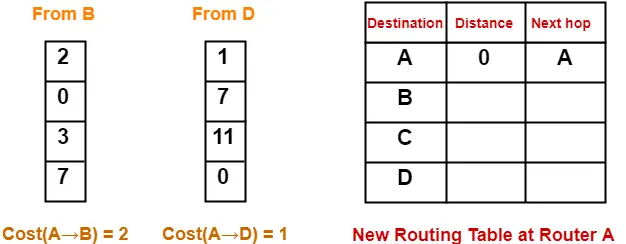
- Cost of reaching destination B from router A = min { 2+0 , 1+7 } = 2 via B.
- Cost of reaching destination C from router A = min { 2+3 , 1+11 } = 5 via B.
- Cost of reaching destination D from router A = min { 2+7 , 1+0 } = 1 via D.
Explanation For Destination B
|
Thus, the new routing table at router A is-
| Destination | Distance | Next Hop |
| A | 0 | A |
| B | 2 | B |
| C | 5 | B |
| D | 1 | D |
At Router B-
- Router B receives distance vectors from its neighbors A, C and D.
- Router B prepares a new routing table as-
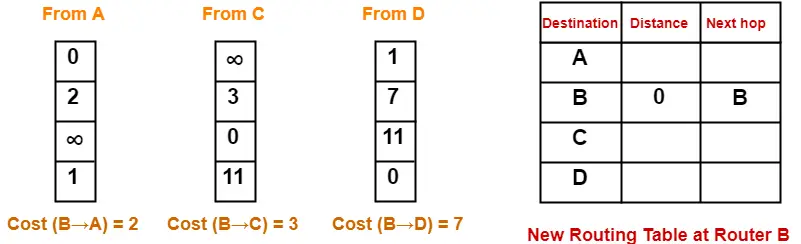
- Cost of reaching destination A from router B = min { 2+0 , 3+∞ , 7+1 } = 2 via A.
- Cost of reaching destination C from router B = min { 2+∞ , 3+0 , 7+11 } = 3 via C.
- Cost of reaching destination D from router B = min { 2+1 , 3+11 , 7+0 } = 3 via A.
Thus, the new routing table at router B is-
| Destination | Distance | Next Hop |
| A | 2 | A |
| B | 0 | B |
| C | 3 | C |
| D | 3 | A |
At Router C-
- Router C receives distance vectors from its neighbors B and D.
- Router C prepares a new routing table as-
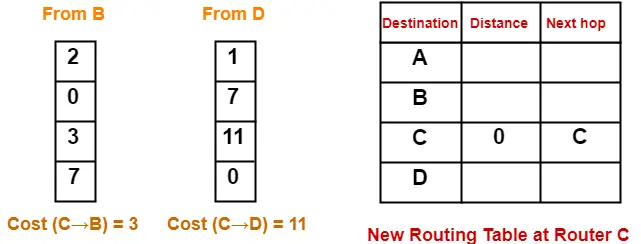
- Cost of reaching destination A from router C = min { 3+2 , 11+1 } = 5 via B.
- Cost of reaching destination B from router C = min { 3+0 , 11+7 } = 3 via B.
- Cost of reaching destination D from router C = min { 3+7 , 11+0 } = 10 via B.
Thus, the new routing table at router C is-
| Destination | Distance | Next Hop |
| A | 5 | B |
| B | 3 | B |
| C | 0 | C |
| D | 10 | B |
At Router D-
- Router D receives distance vectors from its neighbors A, B and C.
- Router D prepares a new routing table as-
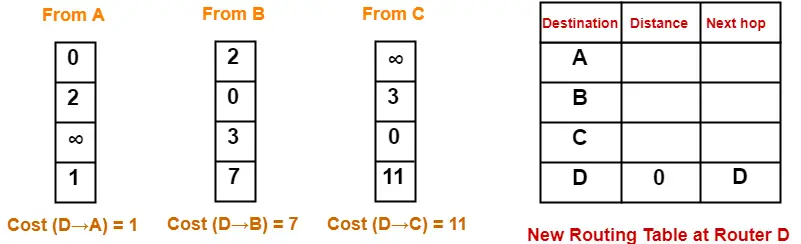
- Cost of reaching destination A from router D = min { 1+0 , 7+2 , 11+∞ } = 1 via A.
- Cost of reaching destination B from router D = min { 1+2 , 7+0 , 11+3 } = 3 via A.
- Cost of reaching destination C from router D = min { 1+∞ , 7+3 , 11+0 } = 10 via B.
Thus, the new routing table at router D is-
| Destination | Distance | Next Hop |
| A | 1 | A |
| B | 3 | A |
| C | 10 | B |
| D | 0 | D |
Step-03:
- Each router exchanges its distance vector obtained in Step-02 with its neighboring routers.
- After exchanging the distance vectors, each router prepares a new routing table.
This is shown below-
At Router A-
- Router A receives distance vectors from its neighbors B and D.
- Router A prepares a new routing table as-
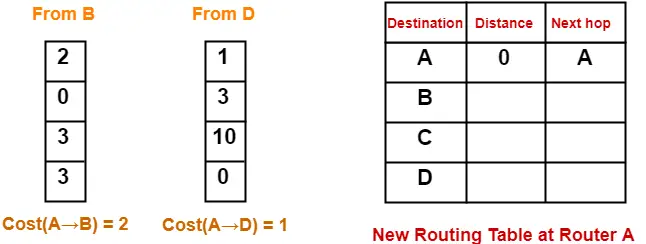
- Cost of reaching destination B from router A = min { 2+0 , 1+3 } = 2 via B.
- Cost of reaching destination C from router A = min { 2+3 , 1+10 } = 5 via B.
- Cost of reaching destination D from router A = min { 2+3 , 1+0 } = 1 via D.
Thus, the new routing table at router A is-
| Destination | Distance | Next Hop |
| A | 0 | A |
| B | 2 | B |
| C | 5 | B |
| D | 1 | D |
At Router B-
- Router B receives distance vectors from its neighbors A, C and D.
- Router B prepares a new routing table as-
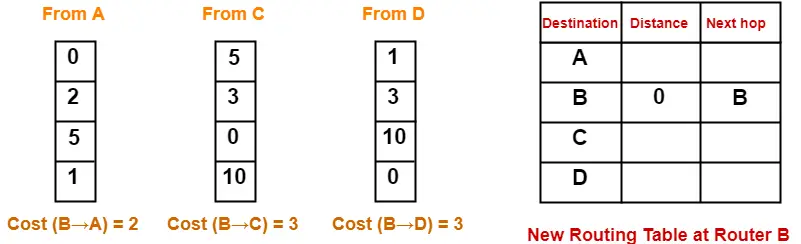
- Cost of reaching destination A from router B = min { 2+0 , 3+5 , 3+1 } = 2 via A.
- Cost of reaching destination C from router B = min { 2+5 , 3+0 , 3+10 } = 3 via C.
- Cost of reaching destination D from router B = min { 2+1 , 3+10 , 3+0 } = 3 via A.
Thus, the new routing table at router B is-
| Destination | Distance | Next Hop |
| A | 2 | A |
| B | 0 | B |
| C | 3 | C |
| D | 3 | A |
At Router C-
- Router C receives distance vectors from its neighbors B and D.
- Router C prepares a new routing table as-
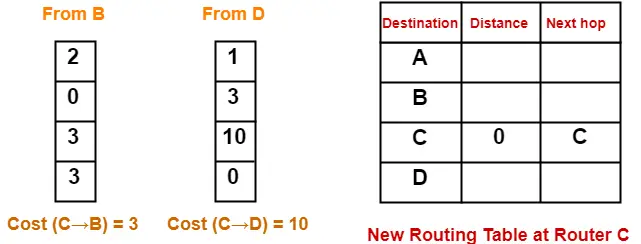
- Cost of reaching destination A from router C = min { 3+2 , 10+1 } = 5 via B.
- Cost of reaching destination B from router C = min { 3+0 , 10+3 } = 3 via B.
- Cost of reaching destination D from router C = min { 3+3 , 10+0 } = 6 via B.
Thus, the new routing table at router C is-
| Destination | Distance | Next Hop |
| A | 5 | B |
| B | 3 | B |
| C | 0 | C |
| D | 6 | B |
At Router D-
- Router D receives distance vectors from its neighbors A, B and C.
- Router D prepares a new routing table as-
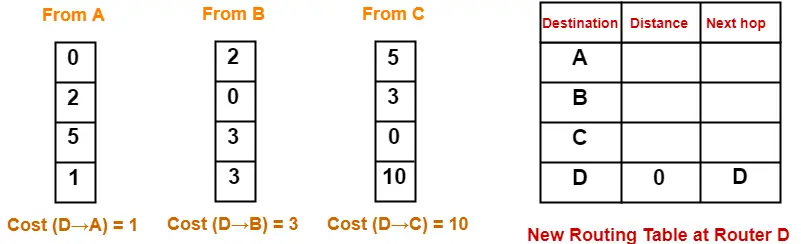
- Cost of reaching destination A from router D = min { 1+0 , 3+2 , 10+5 } = 1 via A.
- Cost of reaching destination B from router D = min { 1+2 , 3+0 , 10+3 } = 3 via A.
- Cost of reaching destination C from router D = min { 1+5 , 3+3 , 10+0 } = 6 via A.
Thus, the new routing table at router D is-
| Destination | Distance | Next Hop |
| A | 1 | A |
| B | 3 | A |
| C | 6 | A |
| D | 0 | D |
These will be the final routing tables at each router.
Identifying Unused Links-
After routing tables converge (becomes stable),
- Some of the links connecting the routers may never be used.
- In the above example, we can identify the unused links as-
We have-
- The value of next hop in the final routing table of router A suggests that only edges AB and AD are used.
- The value of next hop in the final routing table of router B suggests that only edges BA and BC are used.
- The value of next hop in the final routing table of router C suggests that only edge CB is used.
- The value of next hop in the final routing table of router D suggests that only edge DA is used.
Thus, edges BD and CD are never used.
Important Notes-
Note-01:
In Distance Vector Routing,
- Only distance vectors are exchanged.
- “Next hop”values are not exchanged.
- This is because it results in exchanging the large amount of data which consumes more bandwidth.
Note-02:
While preparing a new routing table-
- A router takes into consideration only the distance vectors it has obtained from its neighboring routers.
- It does not take into consideration its old routing table.
Note-03:
The algorithm is called so because-
- It involves exchanging of distance vectors between the routers.
- Distance vector is nothing but an array of distances.
Note-04:
- The algorithm keeps on repeating periodically and never stops.
- This is to update the shortest path in case any link goes down or topology changes.
Note-05:
- Routing tables are prepared total (n-1) times if there are n routers in the given network.
- This is because shortest path between any 2 nodes contains at most n-1 edges if there are n nodes in the graph.
Note-06:
- Distance Vector Routing suffers from count to infinity problem.
- Distance Vector Routing uses UDP at transport layer.
Next Article- IP Address | Classes of IP Address
Get more notes and other study material of Computer Networks.
Watch video lectures by visiting our YouTube channel LearnVidFun.