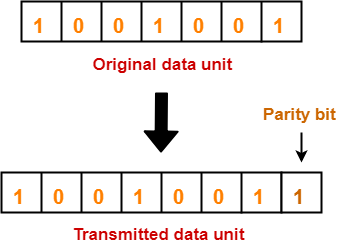
Error Detection in Computer Networks-
| Error detection is a technique that is used to check if any error occurred in the data during the transmission. |
Some popular error detection methods are-
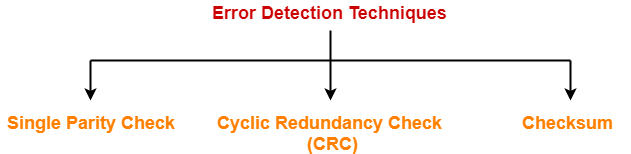
- Single Parity Check
- Cyclic Redundancy Check (CRC)
- Checksum
In this article, we will discuss about Checksum Method.
Checksum-
Checksum is an error detection method.
Error detection using checksum method involves the following steps-
Step-01:
At sender side,
- If m bit checksum is used, the data unit to be transmitted is divided into segments of m bits.
- All the m bit segments are added.
- The result of the sum is then complemented using 1’s complement arithmetic.
- The value so obtained is called as checksum.
Step-02:
- The data along with the checksum value is transmitted to the receiver.
Step-03:
At receiver side,
- If m bit checksum is being used, the received data unit is divided into segments of m bits.
- All the m bit segments are added along with the checksum value.
- The value so obtained is complemented and the result is checked.
Then, following two cases are possible-
Case-01: Result = 0
If the result is zero,
- Receiver assumes that no error occurred in the data during the transmission.
- Receiver accepts the data.
Case-02: Result ≠ 0
If the result is non-zero,
- Receiver assumes that error occurred in the data during the transmission.
- Receiver discards the data and asks the sender for retransmission.
Checksum Example-
Consider the data unit to be transmitted is-
10011001111000100010010010000100
Consider 8 bit checksum is used.
Step-01:
At sender side,
The given data unit is divided into segments of 8 bits as-
![]()
Now, all the segments are added and the result is obtained as-
- 10011001 + 11100010 + 00100100 + 10000100 = 1000100011
- Since the result consists of 10 bits, so extra 2 bits are wrapped around.
- 00100011 + 10 = 00100101 (8 bits)
- Now, 1’s complement is taken which is 11011010.
- Thus, checksum value = 11011010
Step-02:
- The data along with the checksum value is transmitted to the receiver.
Step-03:
At receiver side,
- The received data unit is divided into segments of 8 bits.
- All the segments along with the checksum value are added.
- Sum of all segments + Checksum value = 00100101 + 11011010 = 11111111
- Complemented value = 00000000
- Since the result is 0, receiver assumes no error occurred in the data and therefore accepts it.
Also Read- Parity Check
Important Notes-
Note-01:
- Consider while adding the m bit segments, the result obtained consists of more than m bits.
- Then, wrap around the extra bits and add to the result so that checksum value consists of m bits.
Note-02:
- While calculating the checksum, if checksum value is needed, then assume it to be zero.
- After calculating the checksum value, substitute the checksum value in the checksum field.
- This will be required during checksum calculation of IP Header, TCP Header and UDP Header.
Note-03:
- The checksum is used in the internet by several protocols although not at the data link layer.
Also Read- Cyclic Redundancy Check (CRC)
PRACTICE PROBLEM BASED ON CHECKSUM ERROR DETECTION METHOD-
Problem-
Checksum value of 1001001110010011 and 1001100001001101 of 16 bit segment is-
- 1010101000011111
- 1011111000100101
- 1101010000011110
- 1101010000111111
Solution-
We apply the above discussed algorithm to calculate the checksum.
- 1001001110010011 + 1001100001001101 = 10010101111100000
- Since, the result consists of 17 bits, so 1 bit is wrapped around and added to the result.
- 0010101111100000 + 1 = 0010101111100001
- Now, result consists of 16 bits.
- Now, 1’s complement is taken which is 1101010000011110
- Thus, checksum value = 1101010000011110
Thus, Option (C) is correct.
To gain better understanding about Checksum Method,
Next Article- Access Control Methods | Introduction
Get more notes and other study material of Computer Networks.
Watch video lectures by visiting our YouTube channel LearnVidFun.