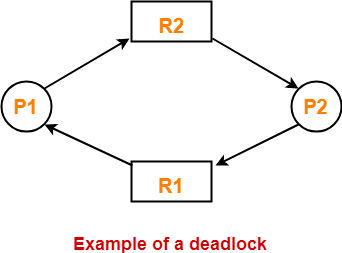
Deadlock in OS-
Before you go through this article, make sure that you have gone through the previous article on Deadlock in OS.
We have discussed-
- In a deadlock state, the execution of multiple processes is blocked.
- There are 4 necessary conditions for the occurrence of deadlock.
- Several Deadlock Handling Strategies exist to deal with the deadlock.
In this article, we will discuss practice problems based on deadlock.
Important Concept-
Consider there are n processes in the system P1, P2, P3, …… , Pn where-
- Process P1 requires x1 units of resource R
- Process P2 requires x2 units of resource R
- Process P3 requires x3 units of resource R and so on.
In worst case,
| The number of units that each process holds = One less than its maximum demand |
So,
- Process P1 holds x1 – 1 units of resource R
- Process P2 holds x2 – 1 units of resource R
- Process P3 holds x3 – 1 units of resource R and so on.
Now,
- Had there been one more unit of resource R in the system, system could be ensured deadlock free.
- This is because that unit would be allocated to one of the processes and it would get execute and then release its units.
From here, we have-
Maximum Number Of Units That Ensures Deadlock-
Maximum number of units of resource R that ensures deadlock
= (x1-1) + (x2-1) + (x3-1) + …. + (xn-1)
= ( x1 + x2 + x3 + …. + xn ) – n
= ∑xi – n
= Sum of max needs of all n processes – n
Minimum Number Of Units That Ensures No Deadlock-
Minimum number of units of resource R that ensures no deadlock
= One more than maximum number of units of resource R that ensures deadlock
= (∑xi – n) + 1
PRACTICE PROBLEMS BASED ON DEADLOCK IN OS-
Problem-01:
A system is having 3 user processes each requiring 2 units of resource R. The minimum number of units of R such that no deadlock will occur-
- 3
- 5
- 4
- 6
Solution-
In worst case,
The number of units that each process holds = One less than its maximum demand
So,
- Process P1 holds 1 unit of resource R
- Process P2 holds 1 unit of resource R
- Process P3 holds 1 unit of resource R
Thus,
- Maximum number of units of resource R that ensures deadlock = 1 + 1 + 1 = 3
- Minimum number of units of resource R that ensures no deadlock = 3 + 1 = 4
Problem-02:
A system is having 10 user processes each requiring 3 units of resource R. The minimum number of units of R such that no deadlock will occur _____?
Solution-
In worst case,
The number of units that each process holds = One less than its maximum demand
So,
- Process P1 holds 2 units of resource R
- Process P2 holds 2 units of resource R
- Process P3 holds 2 units of resource R and so on.
- Process P10 holds 2 units of resource R
Thus,
- Maximum number of units of resource R that ensures deadlock = 10 x 2 = 20
- Minimum number of units of resource R that ensures no deadlock = 20 + 1 = 21
Problem-03:
A system is having 3 user processes P1, P2 and P3 where P1 requires 2 units of resource R, P2 requires 3 units of resource R, P3 requires 4 units of resource R. The minimum number of units of R that ensures no deadlock is _____?
Solution-
In worst case,
The number of units that each process holds = One less than its maximum demand
So,
- Process P1 holds 1 unit of resource R
- Process P2 holds 2 units of resource R
- Process P3 holds 3 units of resource R
Thus,
- Maximum number of units of resource R that ensures deadlock = 1 + 2 + 3 = 6
- Minimum number of units of resource R that ensures no deadlock = 6 + 1 = 7
Problem-04:
A system is having 3 user processes P1, P2 and P3 where P1 requires 21 units of resource R, P2 requires 31 units of resource R, P3 requires 41 units of resource R. The minimum number of units of R that ensures no deadlock is _____?
Solution-
In worst case,
The number of units that each process holds = One less than its maximum demand
So,
- Process P1 holds 20 units of resource R
- Process P2 holds 30 units of resource R
- Process P3 holds 40 units of resource R
Thus,
- Maximum number of units of resource R that ensures deadlock = 20 + 30 + 40 = 90
- Minimum number of units of resource R that ensures no deadlock = 90 + 1 = 91
Problem-05:
If there are 6 units of resource R in the system and each process in the system requires 2 units of resource R, then how many processes can be present at maximum so that no deadlock will occur?
Solution-
In worst case,
The number of units that each process holds = One less than its maximum demand
So,
- Process P1 holds 1 unit of resource R
- Process P2 holds 1 unit of resource R
- Process P3 holds 1 unit of resource R
- Process P4 holds 1 unit of resource R
- Process P5 holds 1 unit of resource R
- Process P6 holds 1 unit of resource R
Thus,
- Minimum number of processes that ensures deadlock = 6
- Maximum number of processes that ensures no deadlock = 6 – 1 = 5
Problem-06:
If there are 6 units of resource R in the system and each process in the system requires 3 units of resource R, then how many processes can be present at maximum so that no deadlock will occur?
Solution-
In worst case,
The number of units that each process holds = One less than its maximum demand
So,
- Process P1 holds 2 units of resource R
- Process P2 holds 2 units of resource R
- Process P3 holds 2 units of resource R
Thus,
- Minimum number of processes that ensures deadlock = 3
- Maximum number of processes that ensures no deadlock = 3 – 1 = 2
Problem-07:
If there are 100 units of resource R in the system and each process in the system requires 2 units of resource R, then how many processes can be present at maximum so that no deadlock will occur?
Solution-
In worst case,
The number of units that each process holds = One less than its maximum demand
So,
- Process P1 holds 1 unit of resource R
- Process P2 holds 1 unit of resource R
- Process P3 holds 1 unit of resource R and so on.
- Process P100 holds 1 unit of resource R
Thus,
- Minimum number of processes that ensures deadlock = 100
- Maximum number of processes that ensures no deadlock = 100 – 1 = 99
Problem-08:
If there are 100 units of resource R in the system and each process in the system requires 4 units of resource R, then how many processes can be present at maximum so that no deadlock will occur?
Solution-
In worst case,
The number of units that each process holds = One less than its maximum demand
So,
- Process P1 holds 3 units of resource R
- Process P2 holds 3 units of resource R
- Process P3 holds 3 units of resource R and so on.
- Process P33 holds 3 units of resource R
- Process P34 holds 1 unit of resource R
Thus,
- Minimum number of processes that ensures deadlock = 34
- Maximum number of processes that ensures no deadlock = 34 – 1 = 33
Problem-09:
If there are 100 units of resource R in the system and each process in the system requires 5 units of resource R, then how many processes can be present at maximum so that no deadlock will occur?
Solution-
In worst case,
The number of units that each process holds = One less than its maximum demand
So,
- Process P1 holds 4 units of resource R
- Process P2 holds 4 units of resource R
- Process P3 holds 4 units of resource R and so on.
- Process P25 holds 4 units of resource R
Thus,
- Minimum number of processes that ensures deadlock = 25
- Maximum number of processes that ensures no deadlock = 25 – 1 = 24
Problem-10:
A computer system has 6 tape drives with n processes competing for them. Each process needs 3 tape drives. The maximum value of n for which the system is guaranteed to be deadlock free-
- 2
- 3
- 4
- 1
Solution-
In worst case,
The number of tape drives that each process holds = One less than its maximum demand
So,
- Process P1 holds 2 tape drives
- Process P2 holds 2 tape drives
- Process P3 holds 2 tape drives
Thus,
- Minimum number of processes that ensures deadlock = 3
- Maximum number of processes that ensures no deadlock = 3 – 1 = 2
Problem-11:
Consider a system having m resources of the same type. These resources are shared by 3 processes A, B and C which have peak demands of 3, 4 and 6 respectively. For what value of m, deadlock will not occur?
- 7
- 9
- 10
- 13
Solution-
In worst case,
The number of units that each process holds = One less than its maximum demand
So,
- Process A holds 2 units of resource R
- Process B holds 3 units of resource R
- Process C holds 5 units of resource R
Thus,
- Maximum number of units of resource R that ensures deadlock = 2 + 3 + 5 = 10
- Minimum number of units of resource R that ensures no deadlock = 10 + 1 = 11
So, any number of units greater than 11 will ensure no deadlock.
Thus, Option (D) is correct.
Problem-12:
Consider a system having m resources of the same type being shared by n processes. Resources can be requested and released by processes only one at a time. The system is deadlock free if and only if-
- The sum of all max needs is < m+n
- The sum of all max needs is > m+n
- Both of above
- None of these
Solution-
We have derived above-
Maximum number of units of resource R that ensures deadlock = (∑xi – n)
Thus, For no deadlock occurrence,
Number of units of resource R must be > (∑xi – n)
i.e. m > (∑xi – n)
or ∑xi < m + n
Thus, Correct Option is (A).
Problem-13:
Consider the following snapshot of a system running n processes. Process i is holding xi instances of a resource R for 1<=i<=n. Currently, all instances of R are occupied. Further, for all i, process i has placed a request for an additional yi instances while holding the xi instances it already has. There are exactly two processes p and q such that yp = yq = 0. Which of the following can serve as a necessary condition to guarantee that the system is not approaching a deadlock?
- min(xp, xq) < maxk≠p,qyk
- xp + xq >= mink≠p,qyk
- min(xp, xq) < 1
- min(xp, xq) >1
Solution-
According to question, we have-
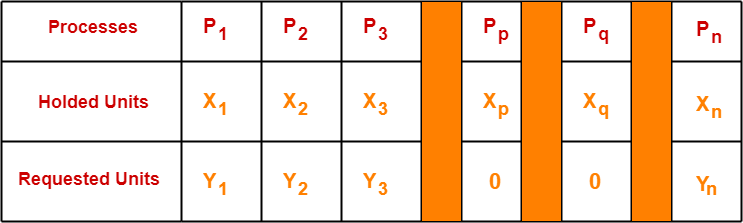
- Clearly, processes Pp and Pq do not require any additional resource.
- So they continue their execution.
- After getting executed completely, they release the units allocated to them.
- Thus, the total units that get free up = xp + xq
Now,
- To ensure that other processes are executed without any deadlock, the total amount of units freely available currently ( xp + xq ) must be able to meet the requirements of some other process.
- If available ( xp + xq ) units could not meet the requirement of any other process, then certainly there would be deadlock.
Thus, for no deadlock, the necessary condition is-
xp + xq >= min yk where k ≠ p, q
Thus, Correct Option is (B).
NOTE-
- It is very important to note that the above condition is just a necessary condition and not at all a sufficient condition to avoid the deadlock.
- The above condition just ensures that the system is able to proceed from the current state.
- It does not guarantee that there won’t be a deadlock before all the other processes are finished.
- The sufficient condition to avoid the deadlock would be either xp + xq >= ∑ yi or xp + xq >= max yk where k ≠ p, q.
To watch video solutions and practice other problems,
Next Article- Banker’s Algorithm
Get more notes and other study material of Operating System.
Watch video lectures by visiting our YouTube channel LearnVidFun.