Magnetic Disk in Computer Architecture-
Before you go through this article, make sure that you have gone through the previous article on Magnetic Disk.
We have discussed-
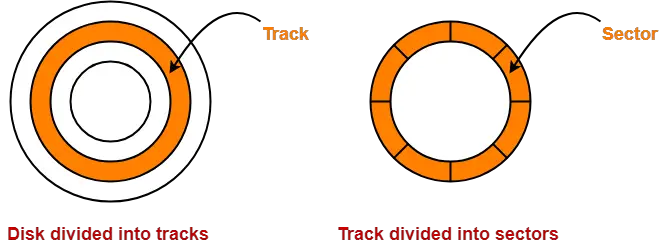
- Magnetic disk is divided into platters which are further divided into tracks and sectors.
- Read / write head is a mechanical arm that is used to write to and read from the disk.
- Various important formulas.
In this article, we will discuss practice problems based on magnetic disk.
PRACTICE PROBLEMS BASED ON MAGNETIC DISK-
Problem-01:
Consider a disk pack with the following specifications- 16 surfaces, 128 tracks per surface, 256 sectors per track and 512 bytes per sector.
Answer the following questions-
- What is the capacity of disk pack?
- What is the number of bits required to address the sector?
- If the format overhead is 32 bytes per sector, what is the formatted disk space?
- If the format overhead is 64 bytes per sector, how much amount of memory is lost due to formatting?
- If the diameter of innermost track is 21 cm, what is the maximum recording density?
- If the diameter of innermost track is 21 cm with 2 KB/cm, what is the capacity of one track?
- If the disk is rotating at 3600 RPM, what is the data transfer rate?
- If the disk system has rotational speed of 3000 RPM, what is the average access time with a seek time of 11.5 msec?
Solution-
Given-
- Number of surfaces = 16
- Number of tracks per surface = 128
- Number of sectors per track = 256
- Number of bytes per sector = 512 bytes
Part-01: Capacity of Disk Pack-
Capacity of disk pack
= Total number of surfaces x Number of tracks per surface x Number of sectors per track x Number of bytes per sector
= 16 x 128 x 256 x 512 bytes
= 228 bytes
= 256 MB
Part-02: Number of Bits Required To Address Sector-
Total number of sectors
= Total number of surfaces x Number of tracks per surface x Number of sectors per track
= 16 x 128 x 256 sectors
= 219 sectors
Thus, Number of bits required to address the sector = 19 bits
Part-03: Formatted Disk Space-
Formatting overhead
= Total number of sectors x overhead per sector
= 219 x 32 bytes
= 219 x 25 bytes
= 224 bytes
= 16 MB
Now, Formatted disk space
= Total disk space – Formatting overhead
= 256 MB – 16 MB
= 240 MB
Part-04: Formatting Overhead-
Amount of memory lost due to formatting
= Formatting overhead
= Total number of sectors x Overhead per sector
= 219 x 64 bytes
= 219 x 26 bytes
= 225 bytes
= 32 MB
Part-05: Maximum Recording Density-
Storage capacity of a track
= Number of sectors per track x Number of bytes per sector
= 256 x 512 bytes
= 28 x 29 bytes
= 217 bytes
= 128 KB
Circumference of innermost track
= 2 x π x radius
= π x diameter
= 3.14 x 21 cm
= 65.94 cm
Now, Maximum recording density
= Recording density of innermost track
= Capacity of a track / Circumference of innermost track
= 128 KB / 65.94 cm
= 1.94 KB/cm
Part-06: Capacity Of Track-
Circumference of innermost track
= 2 x π x radius
= π x diameter
= 3.14 x 21 cm
= 65.94 cm
Capacity of a track
= Storage density of the innermost track x Circumference of the innermost track
= 2 KB/cm x 65.94 cm
= 131.88 KB
≅ 132 KB
Part-07: Data Transfer Rate-
Number of rotations in one second
= (3600 / 60) rotations/sec
= 60 rotations/sec
Now, Data transfer rate
= Number of heads x Capacity of one track x Number of rotations in one second
= 16 x (256 x 512 bytes) x 60
= 24 x 28 x 29 x 60 bytes/sec
= 60 x 221 bytes/sec
= 120 MBps
Part-08: Average Access Time-
Time taken for one full rotation
= (60 / 3000) sec
= (1 / 50) sec
= 0.02 sec
= 20 msec
Average rotational delay
= 1/2 x Time taken for one full rotation
= 1/2 x 20 msec
= 10 msec
Now, average access time
= Average seek time + Average rotational delay + Other factors
= 11.5 msec + 10 msec + 0
= 21.5 msec
Problem-02:
What is the average access time for transferring 512 bytes of data with the following specifications-
- Average seek time = 5 msec
- Disk rotation = 6000 RPM
- Data rate = 40 KB/sec
- Controller overhead = 0.1 msec
Solution-
Given-
- Average seek time = 5 msec
- Disk rotation = 6000 RPM
- Data rate = 40 KB/sec
- Controller overhead = 0.1 msec
Time Taken For One Full Rotation-
Time taken for one full rotation
= (60 / 6000) sec
= (1 / 100) sec
= 0.01 sec
= 10 msec
Average Rotational Delay-
Average rotational delay
= 1/2 x Time taken for one full rotation
= 1/2 x 10 msec
= 5 msec
Transfer Time-
Transfer time
= (512 bytes / 40 KB) sec
= 0.0125 sec
= 12.5 msec
Average Access Time-
Average access time
= Average seek time + Average rotational delay + Transfer time + Controller overhead + Queuing delay
= 5 msec + 5 msec + 12.5 msec + 0.1 msec + 0
= 22.6 msec
Problem-03:
A certain moving arm disk storage with one head has the following specifications-
- Number of tracks per surface = 200
- Disk rotation speed = 2400 RPM
- Track storage capacity = 62500 bits
- Average latency = P msec
- Data transfer rate = Q bits/sec
What is the value of P and Q?
Solution-
Given-
- Number of tracks per surface = 200
- Disk rotation speed = 2400 RPM
- Track storage capacity = 62500 bits
Time Taken For One Full Rotation-
Time taken for one full rotation
= (60 / 2400) sec
= (1 / 40) sec
= 0.025 sec
= 25 msec
Average Latency-
Average latency or Average rotational latency
= 1/2 x Time taken for one full rotation
= 1/2 x 25 msec
= 12.5 msec
Data Transfer Rate-
Data transfer rate
= Number of heads x Capacity of one track x Number of rotations in one second
= 1 x 62500 bits x (2400 / 60)
= 2500000 bits/sec
= 2.5 x 106 bits/sec
Thus, P = 12.5 and Q = 2.5 x 106
Problem-04:
A disk pack has 19 surfaces and storage area on each surface has an outer diameter of 33 cm and inner diameter of 22 cm. The maximum recording storage density on any track is 200 bits/cm and minimum spacing between tracks is 0.25 mm. Calculate the capacity of disk pack.
Solution-
Given-
- Number of surfaces = 19
- Outer diameter = 33 cm
- Inner diameter = 22 cm
- Maximum recording density = 200 bits/cm
- Inter track gap = 0.25 mm
Number Of Tracks On Each Surface-
Number of tracks on each surface
= (Outer radius – Inner radius) / Inter track gap
= (16.5 cm – 11 cm) / 0.25 mm
= 5.5 cm / 0.25 mm
= 55 mm / 0.25 mm
= 220 tracks
Capacity Of Each Track-
Capacity of each track
= Maximum recording density x Circumference of innermost track
= 200 bits/cm x (3.14 x 22 cm)
= 200 x 69.08 bits
= 13816 bits
= 1727 bytes
Capacity Of Disk Pack-
Capacity of disk pack
= Total number of surfaces x Number of tracks per surface x Capacity of one track
= 19 x 220 x 1727 bytes
= 7218860 bytes
= 6.88 MB
Problem-05:
Consider a typical disk that rotates at 15000 RPM and has a transfer rate of 50 x 106 bytes/sec. If the average seek time of the disk is twice the average rotational delay and the controller’s transfer time is 10 times the disk transfer time. What is the average time (in milliseconds) to read or write a 512 byte sector of the disk?
Solution-
Given-
- Rotation speed of the disk = 15000 RPM
- Transfer rate = 50 x 106 bytes/sec
- Average seek time = 2 x Average rotational delay
- Controller’s transfer time = 10 x Disk transfer time
Time Taken For One Full Rotation-
Time taken for one full rotation
= (60 / 15000) sec
= 0.004 sec
= 4 msec
Average Rotational Delay-
Average rotational delay
= 1/2 x Time taken for one full rotation
= 1/2 x 4 msec
= 2 msec
Average Seek Time-
Average seek time
= 2 x Average rotational delay
= 2 x 2 msec
= 4 msec
Disk Transfer Time-
Disk transfer time
= Time taken to read or write 512 bytes
= 512 bytes / (50 x 106 bytes/sec)
= 10.24 x 10-6 sec
= 0.01024 msec
Controller’s Transfer Time-
Controller’s transfer time
= 10 x Disk transfer time
= 10 x 0.01024 msec
= 0.1024 msec
Average Time To Read Or Write 512 Bytes-
Average time to read or write 512 bytes
= Average seek time + Average rotational delay + Disk transfer time + Controller’s transfer time + Queuing delay
= 4 msec + 2 msec + 0.01024 msec + 0.1024 msec + 0
= 6.11 msec
Problem-06:
A hard disk system has the following parameters-
- Number of tracks = 500
- Number of sectors per track = 100
- Number of bytes per sector = 500
- Time taken by the head to move from one track to another adjacent track = 1 msec
- Rotation speed = 600 RPM
What is the average time taken for transferring 250 bytes from the disk?
Solution-
Given-
- Number of tracks = 500
- Number of sectors per track = 100
- Number of bytes per sector = 500
- Time taken by the head to move from one track to another adjacent track = 1 msec
- Rotation speed = 600 RPM
Average Seek Time-
Average seek time
= (Time taken by the head to move from track-1 to track-1 + Time taken by the head to move from track-1 to track-500) / 2
= (0 + 499 x 1 msec) / 2
= 249.5 msec
Time Taken For One Full Rotation-
Time taken for one full rotation
= (60 / 600) sec
= 0.1 sec
= 100 msec
Average Rotational Delay-
Average rotational delay
= 1/2 x Time taken for one full rotation
= 1/2 x 100 msec
= 50 msec
Capacity Of One Track-
Capacity of one track
= Number of sectors per track x Number of bytes per sector
= 100 x 500 bytes
= 50000 bytes
Data Transfer Rate-
Data transfer rate
= Number of heads x Capacity of one track x Number of rotations in one second
= 1 x 50000 bytes x (600 / 60)
= 50000 x 10 bytes/sec
= 5 x 105 bytes/sec
Transfer Time-
Transfer time
= (250 bytes / 5 x 105 bytes) sec
= 50 x 10-5 sec
= 0.5 msec
Average Time Taken To Transfer 250 Bytes-
Average time taken to transfer 250 bytes
= Average seek time + Average rotational delay + Transfer time + Controller overhead + Queuing delay
= 249.5 msec + 50 msec + 0.5 msec + 0 + 0
= 300 msec
Problem-07:
A hard disk has 63 sectors per track, 10 platters each with 2 recording surfaces and 1000 cylinders.
The address of a sector is given as a triple (c, h, s) where c is the cylinder number, h is the surface number and s is the sector number. Thus, the 0th sector is addressed as (0,0,0), the 1st sector as (0,0,1) and so on.
Part-01:
The address <400, 16, 29> corresponds to sector number-
- 505035
- 505036
- 505037
- 505038
Part-02:
The address of 1039 sector is-
- <0, 15, 31>
- <0, 16, 30>
- <0, 16, 31>
- <0, 17, 31>
Solution-
Know this Concept?
In general, when counting of items is started from 0, then-
Example-
If counting is started from 0, then-
|
To solve this question, we assume there is only one track on each surface.
Part-01:
We have to calculate the sector number for the address <400, 16, 29>
Step-01:
To reach our desired cylinder, we have to cross 400 cylinders.
Total number of sectors that are crossed in 400 cylinders
= Number of cylinders x Number of surfaces per cylinder x Number of tracks per surface x Number of sectors per track
= 400 x (10 x 2) x 1 x 63
= 504000
Now, after crossing 400 cylinders (cylinder-0 to cylinder-399), we are at cylinder-400.
Step-02:
To reach our desired surface, we have to cross 16 surfaces.
Total number of sectors that are crossed in 16 surfaces
= Number of surfaces x Number of tracks per surface x Number of sectors per track
= 16 x 1 x 63
= 1008
Now, after crossing 16 surfaces (surface-0 to surface-15) in cylinder-400, we are at surface-16.
Step-03:
To reach our desired sector, we have to cross 29 sectors.
Now, after crossing 29 sectors on surface-16 of cylinder-400, we are at sector-29.
Thus
Total number of sectors that are crossed
= 504000 + 1008 + 29
= 505037
Thus,
- After crossing 505037 sectors, we are at sector-505037.
- So, required address of the sector is 505037.
- Option (C) is correct.
Part-02:
We have to find the address of the sector-2039.
Let us check all the options one by one.
Option-A:
For the address <0, 15, 31>, the sector number is-
Sector number = 0 + (15 x 1 x 63) + 31 = 976
Option-B:
For the address <0, 16, 30>, the sector number is-
Sector number = 0 + (16 x 1 x 63) + 30 = 1038
Option-C:
For the address <0, 16, 31>, the sector number is-
Sector number = 0 + (16 x 1 x 63) + 31 = 1039
Option-D:
For the address <0, 17, 31>, the sector number is-
Sector number = 0 + (17 x 1 x 63) + 31 = 1102
Thus, Option (C) is correct.
Next Article- Addressing Modes
Get more notes and other study material of Computer Organization and Architecture.
Watch video lectures by visiting our YouTube channel LearnVidFun.