Cryptography in Network Security-
Before you go through this article, make sure that you have gone through the previous article on Cryptography.
We have discussed-
- Cryptography is a method of storing and transmitting data in a particular form.
- Cryptography techniques are-

In this article, we will discuss about Asymmetric Key Cryptography.
Asymmetric Key Cryptography-
In this technique,
- Sender and receiver use different keys to encrypt and decrypt the message.
- It is called so because sender and receiver use different keys.
- It is also called as public key cryptography.
Working-
The message exchange using public key cryptography involves the following steps-
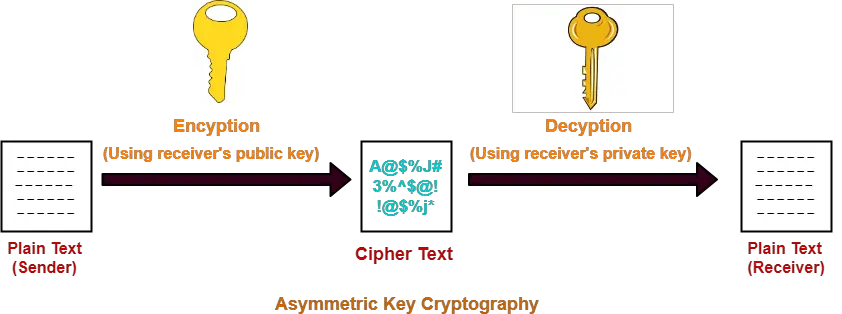
Step-01:
At sender side,
- Sender encrypts the message using receiver’s public key.
- The public key of receiver is publicly available and known to everyone.
- Encryption converts the message into a cipher text.
- This cipher text can be decrypted only using the receiver’s private key.
Step-02:
- The cipher text is sent to the receiver over the communication channel.
Step-03:
At receiver side,
- Receiver decrypts the cipher text using his private key.
- The private key of the receiver is known only to the receiver.
- Using the public key, it is not possible for anyone to determine the receiver’s private key.
- After decryption, cipher text converts back into a readable format.
Advantages-
The advantages of public key cryptography are-
- It is more robust.
- It is less susceptible to third-party security breach attempts.
Disadvantages-
The disadvantages of public key cryptography are-
- It involves high computational requirements.
- It is slower than symmetric key cryptography.
Number of Keys Required-
To use public key cryptography,
- Each individual requires two keys- one public key and one private key.
- For n individuals to communicate, number of keys required = 2 x n = 2n keys.
Asymmetric Encryption Algorithms-
The famous asymmetric encryption algorithms are-

- RSA Algorithm
- Diffie-Hellman Key Exchange
In this article, we will discuss about RSA Algorithm.
RSA Algorithm-
Let-
- Public key of the receiver = (e , n)
- Private key of the receiver = (d , n)
Then, RSA Algorithm works in the following steps-
Step-01:
At sender side,
- Sender represents the message to be sent as an integer between 0 and n-1.
- Sender encrypts the message using the public key of receiver.
- It raises the plain text message ‘P’ to the eth power modulo n.
- This converts the message into cipher text ‘C’.
| C = Pe mod n |
Step-02:
- The cipher text ‘C’ is sent to the receiver over the communication channel.
Step-03:
At receiver side,
- Receiver decrypts the cipher text using his private key.
- It raises the cipher text ‘C’ to the dth power modulo n.
- This converts the cipher text back into the plain text ‘P’.
| P = Cd mod n |
NOTE-
‘e’ and ‘d’ must be multiplicative inverses modulo Ø(n)
After decryption, receiver must have- P = Cd mod n P = (Pe mod n)d mod n P = Ped mod n For this equation to be true, by Euler’s Theorem, we must have- ed = 1 mod Ø(n) OR ed = kØ(n) + 1 Thus, e and d must be multiplicative inverses modulo Ø(n). |
Steps to Generate Public Key And Private Key-
An individual can generate his public key and private key using the following steps-
Step-01:
Choose any two prime numbers p and q such that-
- They are different.
- They are very large.
Step-02:
Calculate ‘n’ and toilent function Ø(n) where-
- n = p x q
- Ø(n) = (p-1) x (q-1)
Step-03:
Choose any value of ‘e’ such that-
- 1 < e < Ø(n)
- gcd (e, Ø(n)) = 1
Step-04:
Determine ‘d’ such that-

- You already know the value of ‘e’ and Ø(n).
- Choose the least positive integer value of ‘k’ which gives the integer value of ‘d’ as a result.
- Use trial and error method.
- Start substituting different values of ‘k’ from 0.
PRACTICE PROBLEMS BASED ON RSA ALGORITHM-
Problem-01:
In a RSA cryptosystem, a participant A uses two prime numbers p = 13 and q = 17 to generate her public and private keys. If the public key of A is 35, then the private key of A is _______.
Solution-
Given-
- Prime numbers p = 13 and q = 17
- Public key = 35
Step-01:
Calculate ‘n’ and toilent function Ø(n).
Value of n,
n = p x q
n = 13 x 17
∴ n = 221
Toilent function,
Ø(n) = (p-1) x (q-1)
Ø(n) = (13-1) x (17-1)
∴ Ø(n) = 192
Step-02:
- We are already given the value of e = 35.
- Thus, public key = (e , n) = (35 , 221)
Step-03:
Determine ‘d’ such that-
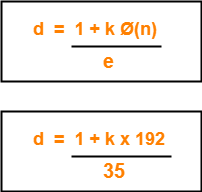
Here,
- The least value of ‘k’ which gives the integer value of ‘d’ is k = 2.
- On substituting k = 2, we get d = 11.
Thus, private key of participant A = (d , n) = (11, 221).
Problem-02:
In the RSA public key cryptosystem, the private and public keys are (e, n) and (d, n) respectively, where n = p x q and p and q are large primes. Besides, n is public and p and q are private. Let M be an integer such that 0 < M < n and f(n) = (p-1)(q-1).
Now consider the following equations-
I. M’ = Me mod n and M = (M’)d mod n
II. ed ≡ 1 mod n
III. ed = 1 mod f(n)
IV. M’ = Me mod f(n) and M = (M’)d mod f(n)
Which of the above equations correctly represent RSA cryptosystem?
- I and II
- I and III
- II and IV
- III and IV
Solution-
Clearly, Option (B) is correct.
To gain better understanding about RSA Algorithm,
Next Article- Diffie Hellman Key Exchange Algorithm
Get more notes and other study material of Computer Networks.
Watch video lectures by visiting our YouTube channel LearnVidFun.