Symmetric Encryption Example

Tag: Symmetric Encryption Example

Diffie Hellman Key Exchange | Asymmetric Encryption

Asymmetric Encryption-

Before you go through this article, make sure that you have gone through the previous article on Asymmetric Key Cryptography.

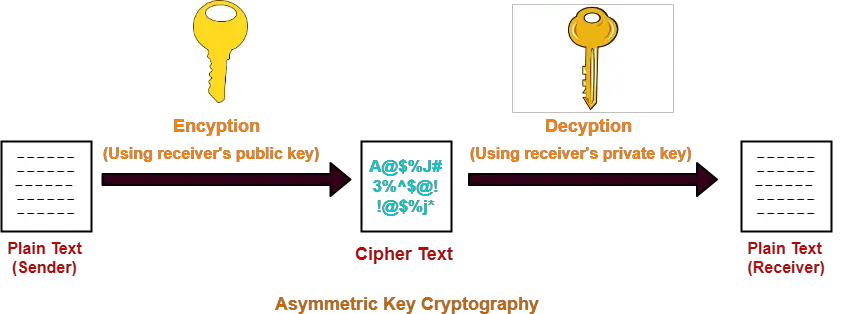
In asymmetric encryption,

Sender and receiver use different keys to encrypt and decrypt the message.
The famous asymmetric encryption algorithms are-

In this article, we will discuss about Diffie Hellman Key Exchange Algorithm.

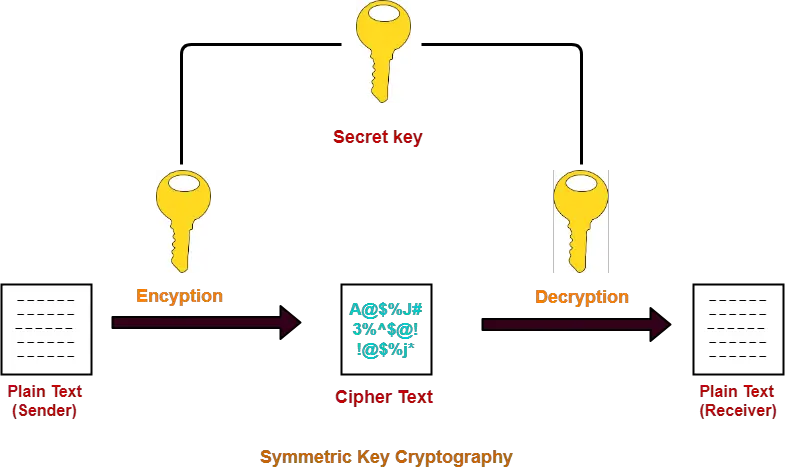
Symmetric Key Cryptography-

In symmetric key cryptography,

Both sender and receiver use a common secret key to encrypt and decrypt the message.
The major issue is exchanging the secret key between the sender and the receiver.
Attackers might intrude and know the secret key while exchanging it.

Read More- Symmetric Key Cryptography

Diffie Hellman Key Exchange-

As the name suggests,

This algorithm is used to exchange the secret key between the sender and the receiver.
This algorithm facilitates the exchange of secret key without actually transmitting it.

Diffie Hellman Key Exchange Algorithm-

Let-

Private key of the sender = X_s
Public key of the sender = Y_s
Private key of the receiver = X_r
Public key of the receiver = Y_r

Using Diffie Hellman Algorithm, the key is exchanged in the following steps-

Step-01:

One of the parties choose two numbers ‘a’ and ‘n’ and exchange with the other party.
‘a’ is the primitive root of prime number ‘n’.
After this exchange, both the parties know the value of ‘a’ and ‘n’.

Step-02:

Both the parties already know their own private key.
Both the parties calculate the value of their public key and exchange with each other.

Sender calculate its public key as-

Y_s = a^X_s mod n

Receiver calculate its public key as-

Y_r = a^X_r mod n

Step-03:

Both the parties receive public key of each other.
Now, both the parties calculate the value of secret key.

Sender calculates secret key as-

Secret key = (Y_r)^X_s mod n

Receiver calculates secret key as-

Secret key = (Y_s)^X_r mod n

Finally, both the parties obtain the same value of secret key.

PRACTICE PROBLEMS BASED ON DIFFIE HELLMAN KEY EXCHANGE-

Problem-01:

Suppose that two parties A and B wish to set up a common secret key (D-H key) between themselves using the Diffie Hellman key exchange technique. They agree on 7 as the modulus and 3 as the primitive root. Party A chooses 2 and party B chooses 5 as their respective secrets. Their D-H key is-

Solution-

Given-

n = 7
a = 3
Private key of A = 2
Private key of B = 5

Step-01:

Both the parties calculate the value of their public key and exchange with each other.

Public key of A

= 3^{private key of A} mod 7

= 3² mod 7

= 2

Public key of B

= 3^{private key of B} mod 7

= 3⁵ mod 7

= 5

Step-02:

Both the parties calculate the value of secret key at their respective side.

Secret key obtained by A

= 5^{private key of A} mod 7

= 5² mod 7

= 4

Secret key obtained by B

= 2^{private key of B} mod 7

= 2⁵ mod 7

= 4

Finally, both the parties obtain the same value of secret key.

The value of common secret key = 4.

Thus, Option (B) is correct.

Problem-02:

In a Diffie-Hellman Key Exchange, Alice and Bob have chosen prime value q = 17 and primitive root = 5. If Alice’s secret key is 4 and Bob’s secret key is 6, what is the secret key they exchanged?

Solution-

Given-

n = 17
a = 5
Private key of Alice = 4
Private key of Bob = 6

Step-01:

Both Alice and Bob calculate the value of their public key and exchange with each other.

Public key of Alice

= 5^{private key of Alice} mod 17

= 5⁴ mod 17

= 13

Public key of Bob

= 5^{private key of Bob} mod 17

= 5⁶ mod 17

= 2

Step-02:

Both the parties calculate the value of secret key at their respective side.

Secret key obtained by Alice

= 2^{private key of Alice} mod 7

= 2⁴ mod 17

= 16

Secret key obtained by Bob

= 13^{private key of Bob} mod 7

= 13⁶ mod 17

= 16

Finally, both the parties obtain the same value of secret key.

The value of common secret key = 16.

Thus, Option (A) is correct.

To gain better understanding about Diffie Hellman Key Exchange Algorithm,

Watch this Video Lecture

Next Article- Digital Signatures

Get more notes and other study material of Computer Networks.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Public Key Cryptography | RSA Algorithm Example

Computer Networks

Cryptography in Network Security-

Before you go through this article, make sure that you have gone through the previous article on Cryptography.

We have discussed-

Cryptography is a method of storing and transmitting data in a particular form.
Cryptography techniques are-

In this article, we will discuss about Asymmetric Key Cryptography.

Asymmetric Key Cryptography-

In this technique,

Sender and receiver use different keys to encrypt and decrypt the message.
It is called so because sender and receiver use different keys.
It is also called as public key cryptography.

Working-

The message exchange using public key cryptography involves the following steps-

Step-01:

At sender side,

Sender encrypts the message using receiver’s public key.
The public key of receiver is publicly available and known to everyone.
Encryption converts the message into a cipher text.
This cipher text can be decrypted only using the receiver’s private key.

Step-02:

The cipher text is sent to the receiver over the communication channel.

Step-03:

At receiver side,

Receiver decrypts the cipher text using his private key.
The private key of the receiver is known only to the receiver.
Using the public key, it is not possible for anyone to determine the receiver’s private key.
After decryption, cipher text converts back into a readable format.

Advantages-

The advantages of public key cryptography are-

It is more robust.
It is less susceptible to third-party security breach attempts.

Disadvantages-

The disadvantages of public key cryptography are-

It involves high computational requirements.
It is slower than symmetric key cryptography.

Number of Keys Required-

To use public key cryptography,

Each individual requires two keys- one public key and one private key.
For n individuals to communicate, number of keys required = 2 x n = 2n keys.

Asymmetric Encryption Algorithms-

The famous asymmetric encryption algorithms are-

RSA Algorithm
Diffie-Hellman Key Exchange

In this article, we will discuss about RSA Algorithm.

RSA Algorithm-

Let-

Public key of the receiver = (e , n)
Private key of the receiver = (d , n)

Then, RSA Algorithm works in the following steps-

Step-01:

At sender side,

Sender represents the message to be sent as an integer between 0 and n-1.
Sender encrypts the message using the public key of receiver.
It raises the plain text message ‘P’ to the e^th power modulo n.
This converts the message into cipher text ‘C’.

C = P^e mod n

Step-02:

The cipher text ‘C’ is sent to the receiver over the communication channel.

Step-03:

At receiver side,

Receiver decrypts the cipher text using his private key.
It raises the cipher text ‘C’ to the d^th power modulo n.
This converts the cipher text back into the plain text ‘P’.

P = C^d mod n

NOTE-

‘e’ and ‘d’ must be multiplicative inverses modulo Ø(n)

After decryption, receiver must have-

P = C^d mod n

P = (P^e mod n)^d mod n

P = P^ed mod n

For this equation to be true, by Euler’s Theorem, we must have-

ed = 1 mod Ø(n)

ed = kØ(n) + 1

Thus, e and d must be multiplicative inverses modulo Ø(n).

Steps to Generate Public Key And Private Key-

An individual can generate his public key and private key using the following steps-

Step-01:

Choose any two prime numbers p and q such that-

They are different.
They are very large.

Step-02:

Calculate ‘n’ and toilent function Ø(n) where-

n = p x q
Ø(n) = (p-1) x (q-1)

Step-03:

Choose any value of ‘e’ such that-

1 < e < Ø(n)
gcd (e, Ø(n)) = 1

Step-04:

Determine ‘d’ such that-

You already know the value of ‘e’ and Ø(n).
Choose the least positive integer value of ‘k’ which gives the integer value of ‘d’ as a result.
Use trial and error method.
Start substituting different values of ‘k’ from 0.

PRACTICE PROBLEMS BASED ON RSA ALGORITHM-

Problem-01:

In a RSA cryptosystem, a participant A uses two prime numbers p = 13 and q = 17 to generate her public and private keys. If the public key of A is 35, then the private key of A is _______.

Solution-

Given-

Prime numbers p = 13 and q = 17
Public key = 35

Step-01:

Calculate ‘n’ and toilent function Ø(n).

Value of n,

n = p x q

n = 13 x 17

∴ n = 221

Toilent function,

Ø(n) = (p-1) x (q-1)

Ø(n) = (13-1) x (17-1)

∴ Ø(n) = 192

Step-02:

We are already given the value of e = 35.
Thus, public key = (e , n) = (35 , 221)

Step-03:

Determine ‘d’ such that-

Here,

The least value of ‘k’ which gives the integer value of ‘d’ is k = 2.
On substituting k = 2, we get d = 11.

Thus, private key of participant A = (d , n) = (11, 221).

Problem-02:

In the RSA public key cryptosystem, the private and public keys are (e, n) and (d, n) respectively, where n = p x q and p and q are large primes. Besides, n is public and p and q are private. Let M be an integer such that 0 < M < n and f(n) = (p-1)(q-1).

Now consider the following equations-

I. M’ = M^e mod n and M = (M’)^d mod n

II. ed ≡ 1 mod n

III. ed = 1 mod f(n)

IV. M’ = M^e mod f(n) and M = (M’)^d mod f(n)

Which of the above equations correctly represent RSA cryptosystem?

I and II
I and III
II and IV
III and IV

Solution-

Clearly, Option (B) is correct.

To gain better understanding about RSA Algorithm,

Watch this Video Lecture

Next Article- Diffie Hellman Key Exchange Algorithm

Get more notes and other study material of Computer Networks.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Symmetric Key Cryptography | Cryptography Techniques

Computer Networks

Cryptography in Network Security-

In network security,

Cryptography is a method of storing and transmitting data in a particular form.
It ensures that only the person for whom the message is intended can read the message.

The message exchange using cryptography involves the following steps-

Step-01:

At sender side,

Using an encryption algorithm, the message is converted into an unreadable form.
The message in unreadable form is called as cipher text.

Step-02:

The cipher text is sent to the receiver over the communication channel.
Since the message is encrypted, the attackers can not read the message.

Step-03:

At receiver side,

Using a decryption algorithm, the message is again converted into the readable form.
Then, receiver can read the message.

Cryptography Techniques-

Cryptography techniques may be classified as-

Symmetric Key Cryptography
Asymmetric Key Cryptography

In this article, we will discuss about symmetric key cryptography.

Symmetric Key Cryptography-

In this technique,

Both sender and receiver uses a common key to encrypt and decrypt the message.
This secret key is known only to the sender and to the receiver.
It is also called as secret key cryptography.

Working-

The message exchange using symmetric key cryptography involves the following steps-

Before starting the communication, sender and receiver shares the secret key.
This secret key is shared through some external means.
At sender side, sender encrypts the message using his copy of the key.
The cipher text is then sent to the receiver over the communication channel.
At receiver side, receiver decrypts the cipher text using his copy of the key.
After decryption, the message converts back into readable format.

Symmetric Encryption Algorithms-

Some of the encryption algorithms that use symmetric key are-

Advanced Encryption Standard (AES)
Data Encryption Standard (DES)

Advantages-

The advantages of symmetric key algorithms are-

They are efficient.
They take less time to encrypt and decrypt the message.

Disadvantages-

Point-01:

The number of keys required is very large.

In symmetric key cryptography,

Each pair of users require a unique secret key.
If N people in the world wants to use this technique, then there needs to be N(N-1) / 2 secret keys.
For 1 million people to communicate, a half billion secret keys would be needed.

How N(N-1)/2 Keys Will Be Required?

Consider a complete graph with N nodes.
Consider each node represents one person.
Then, each person will require (N-1) keys to communicate with other (N-1) people.
Thus, each edge must have a unique key for communication.
Thus, Number of keys required = Number of edges = ⁿC₂ = n(n-1)/2.

Point-02:

Sharing the secret key between the sender and receiver is an important issue.
While sharing the key, attackers might intrude.

To overcome this disadvantage,

Diffie Hellman Key Exchange Algorithm is used for exchanging the secret key.

Important Points-

Point-01:

In symmetric key cryptography,

Both sender and receiver uses the same key.
Sender encrypts the message using his copy of the key.
Receiver decrypts the message using his copy of the key.
The key must not be known to anyone else other than sender and receiver.
If the secret key is known to any intruder, he could decrypt the message.

Point-02:

This cryptography technique is called as symmetric key cryptography.
It is because both sender and receiver use the same key on their sides.

Point-03:

This cryptography technique is called as secret key cryptography.
It is because the key has to be kept secret between the sender and receiver.

To gain better understanding about Symmetric Key Cryptography,

Watch this Video Lecture

Next Article- Asymmetric Key Cryptography | RSA Algorithm

Get more notes and other study material of Computer Networks.

Watch video lectures by visiting our YouTube channel LearnVidFun.