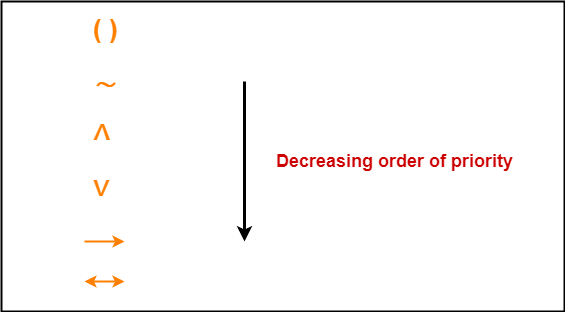
Propositions-
Before you go through this article, make sure that you have gone through the previous article on Propositions.
We have discussed-
- Propositions are declarative statements that are either true or false but not both.
- Connectives are used to combine the propositions.

In this article, we will discuss about the nature of proposition.
Also Read- Converting English Sentences to Propositional Logic
Determining Nature Of Proposition-
Here,
- We will be given a compound proposition.
- We will be asked to determine the nature of the given proposition.

Let us discuss all these terms one by one.
Tautology-
- A compound proposition is called tautology if and only if it is true for all possible truth values of its propositional variables.
- It contains only T (Truth) in last column of its truth table.
Contradiction-
- A compound proposition is called contradiction if and only if it is false for all possible truth values of its propositional variables.
- It contains only F (False) in last column of its truth table.
Contingency-
- A compound proposition is called contingency if and only if it is neither a tautology nor a contradiction.
- It contains both T (True) and F (False) in last column of its truth table.
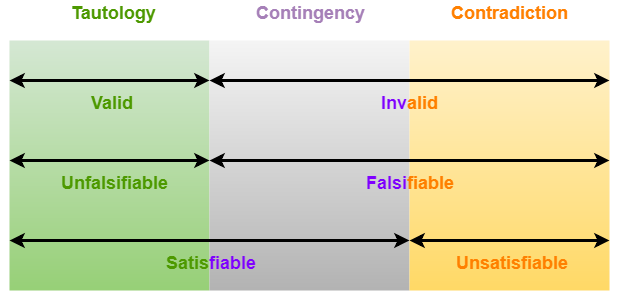
Valid-
- A compound proposition is called valid if and only if it is a tautology.
- It contains only T (Truth) in last column of its truth table.
Invalid-
- A compound proposition is called invalid if and only if it is not a tautology.
- It contains either only F (False) or both T (Truth) and F (False) in last column of its truth table.
Falsifiable-
- A compound proposition is called falsifiable if and only if it can be made false for some value of its propositional variables.
- It contains either only F (False) or both T (Truth) and F (False) in last column of its truth table.
Unfalsifiable-
- A compound proposition is called unfalsifiable if and only if it can never be made false for any value of its propositional variables.
- It contains only T (Truth) in last column of its truth table.
Satisfiable-
- A compound proposition is called satisfiable if and only if it can be made true for some value of its propositional variables.
- It contains either only T (Truth) or both T (True) and F (False) in last column of its truth table.
Unsatisfiable-
- A compound proposition is called unsatisfiable if and only if it can not be made true for any value of its propositional variables.
- It contains only F (False) in last column of its truth table.
Important Points-
It is important to take a note of the the following points-
- All contradictions are invalid and falsifiable but not vice-versa.
- All contingencies are invalid and falsifiable but not vice-versa.
- All tautologies are valid and unfalsifiable and vice-versa.
- All tautologies are satisfiable but not vice-versa.
- All contingencies are satisfiable but not vice-versa.
- All contradictions are unsatisfiable and vice-versa.
Also Read- Converse, Inverse and Contrapositive
PRACTICE PROBLEMS BASED ON DETERMINING NATURE OF PROPOSITIONS-
Problem-01:
Determine the nature of following propositions-
- p ∧ ∼p
- (p ∧ (p → q)) → ∼q
- [ (p → q) ∧ (q → r) ] ∧ ( p ∧ ∼r)
- ∼(p → q) ∨ (∼p ∨ (p ∧ q))
- (p ↔ r) → (∼q → (p ∧ r))
Solution-
Let us solve all the parts one by one-
Part-01:
Method-01: Using Truth Table-
| p | ∼p | p ∧ ∼p |
| F | T | F |
| T | F | F |
Clearly, last column of the truth table contains only F.
Therefore, given proposition is-
- Contradiction
- Invalid
- Falsifiable
- Unsatisfiable
Method-02: Using Algebra Of Proposition-
- The given proposition is p ∧ ∼p
- By complement law, p ∧ ∼p = F
- So, given proposition is contradiction, invalid, falsifiable and unsatisfiable.
Method-03: Using Digital Electronics-
In terms of digital electronics,
- The given proposition can be written as p.p’
- Clearly, p.p’ = 0
- So, given proposition is contradiction, invalid, falsifiable and unsatisfiable.
Part-02:
Method-01: Using Truth Table-
| p | q | p → q | p ∧ (p → q) | ∼q | (p ∧ (p → q)) →∼q |
| F | F | T | F | T | T |
| F | T | T | F | F | T |
| T | F | F | F | T | T |
| T | T | T | T | F | F |
Clearly, last column of the truth table contains both T and F.
Therefore, given proposition is-
- Contingency
- Invalid
- Falsifiable
- Satisfiable
Method-02: Using Algebra Of Proposition-
We have-
(p ∧ (p → q)) → ∼q
= (p ∧ (∼p ∨ q)) → ∼q { ∵ p → q = ∼p ∨ q }
= ∼(p ∧ (∼p ∨ q)) ∨ ∼q { ∵ p → q = ∼p ∨ q }
= ∼((p ∧ ∼p) ∨ (p ∧ q)) ∨ ∼q { Using Distributive law }
= ∼(F ∨ (p ∧ q)) ∨ ∼q { Using Complement law }
= ∼(p ∧ q) ∨ ∼q { Using Identity law }
= ∼p ∨ ∼q ∨ ∼q { Using De Morgans law }
= ∼p ∨ ∼q
- Clearly, the result is neither T nor F.
- So, given proposition is a contingency, invalid, falsifiable and satisfiable.
Method-03: Using Digital Electronics-
We have-
(p ∧ (p → q)) → ∼q
= (p ∧ (∼p ∨ q)) → ∼q { ∵ p → q = ∼p ∨ q }
= ∼(p ∧ (∼p ∨ q)) ∨ ∼q { ∵ p → q = ∼p ∨ q }
Now in terms of digital electronics, we have-
= (p.(p’ + q))’ + q’
= (p.p’ + p.q)’ + q’
= (p.q)’ + q’ { ∵ p.p’ = 0 }
= p’ + q’ + q’ { Using De Morgan’s law }
= p’ + q’
- Clearly, the result is neither 0 nor 1.
- So, given proposition is a contingency, invalid, falsifiable and satisfiable.
Part-03:
Method-01: Using Truth Table-
Let [ (p → q) ∧ (q → r) ] ∧ ( p ∧ ∼r) = R (say)
| p | q | r | p → q | q → r | (p → q) ∧ (q → r) | p ∧ ∼r | R |
| F | F | F | T | T | T | F | F |
| F | F | T | T | T | T | F | F |
| F | T | F | T | F | F | F | F |
| F | T | T | T | T | T | F | F |
| T | F | F | F | T | F | T | F |
| T | F | T | F | T | F | F | F |
| T | T | F | T | F | F | T | F |
| T | T | T | T | T | T | F | F |
Clearly, last column of the truth table contains only F.
Therefore, given proposition is-
- Contradiction
- Invalid
- Falsifiable
- Unsatisfiable
Method-02: Using Algebra Of Proposition-
We have-
[ (p → q) ∧ (q → r) ] ∧ ( p ∧ ∼r)
= [ (∼p ∨ q) ∧ (∼q ∨ r) ] ∧ ( p ∧ ∼r) { ∵ p → q = ∼p ∨ q }
= [ ((∼p ∨ q) ∧ ∼q) ∨ ((∼p ∨ q) ∧ r) ] ∧ ( p ∧ ∼r) { Using Distributive law }
= [ ((∼p ∧ ∼q) ∨ (q ∧ ∼q)) ∨ ((∼p ∧ r) ∨ (q ∧ r)) ] ∧ ( p ∧ ∼r) { Using Distributive law }
= [ ((∼p ∧ ∼q) ∨ F) ∨ ((∼p ∧ r) ∨ (q ∧ r)) ] ∧ ( p ∧ ∼r) { Using Complement law }
= [ (∼p ∧ ∼q) ∨ (∼p ∧ r) ∨ (q ∧ r) ] ∧ ( p ∧ ∼r) { Using Identity law }
= ((∼p ∧ ∼q) ∧ ( p ∧ ∼r)) ∨ ((∼p ∧ r) ∧ ( p ∧ ∼r)) ∨ ((q ∧ r) ∧ ( p ∧ ∼r)) { Using Distributive law }
= (∼p ∧ ∼q ∧ p ∧ ∼r) ∨ (∼p ∧ r ∧ p ∧ ∼r) ∨ (q ∧ r ∧ p ∧ ∼r)
= F ∨ F ∨ F { Using Complement law }
= F
- Clearly, the result is F.
- So, given proposition is a contradiction, invalid, falsifiable and unsatisfiable.
Method-03: Using Digital Electronics-
We have-
[ (p → q) ∧ (q → r) ] ∧ ( p ∧ ∼r)
= [ (∼p ∨ q) ∧ (∼q ∨ r) ] ∧ ( p ∧ ∼r) { ∵ p → q = ∼p ∨ q }
Now in terms of digital electronics, we have-
= [ (p’ + q).(q’ + r) ] . (p.r’)
= [ p’.q’ + p’.r + q.q’ + q.r ] . (p.r’)
= [ p’.q’ + p’.r + 0 + q.r ] . (p.r’) { ∵ q.q’ = 0 }
= [ p’.q’ + p’.r + q.r ] . (p.r’)
= p’.q’.p.r’ + p’.r.p.r’ + q.r.p.r’
= 0 + 0 + 0
= 0
- Clearly, the result is 0.
- So, given proposition is a contradiction, invalid, falsifiable and unsatisfiable.
Part-04:
Method-01: Using Truth Table-
Let ∼(p → q) ∨ (∼p ∨ (p ∧ q)) = R (say)
| p | q | ∼p |
p → q | ∼(p → q) | p ∧ q | ∼p ∨ (p ∧ q) |
R |
| F | F | T | T | F | F | T | T |
| F | T | T | T | F | F | T | T |
| T | F | F | F | T | F | F | T |
| T | T | F | T | F | T | T | T |
Clearly, last column of the truth table contains only T.
Therefore, given proposition is-
- Tautology
- Valid
- Unfalsifiable
- Satisfiable
Method-02: Using Algebra Of Proposition-
We have-
∼(p → q) ∨ (∼p ∨ (p ∧ q))
= ∼(∼p ∨ q) ∨ (∼p ∨ (p ∧ q)) { ∵ p → q = ∼p ∨ q }
= (p ∧ ∼q) ∨ (∼p ∨ (p ∧ q)) { Using De Morgans law }
= (p ∧ ∼q) ∨ ((∼p ∨ p) ∧ (∼p ∨ q)) { Using Distributive law }
= (p ∧ ∼q) ∨ (T ∧ (∼p ∨ q)) { Using Complement law }
= (p ∧ ∼q) ∨ (∼p ∨ q) { Using Identity law }
= ((p ∧ ∼q) ∨ ∼p) ∨ q { Using Associative law }
= ((p ∨ ∼p) ∧ (∼q ∨ ∼p)) ∨ q { Using Distributive law }
= (T ∧ (∼q ∨ ∼p)) ∨ q { Using Complement law }
= (∼q ∨ ∼p) ∨ q { Using Identity law }
= ∼p ∨ (q ∨ ∼q)
= ∼p ∨ T { Using Complement law }
= T { Using Identity law }
- Clearly, the result is T.
- So, given proposition is a tautology, valid, unfalsifiable and satisfiable.
Method-03: Using Digital Electronics-
We have-
∼(p → q) ∨ (∼p ∨ (p ∧ q))
= ∼(∼p ∨ q) ∨ (∼p ∨ (p ∧ q)) { ∵ p → q = ∼p ∨ q }
Now in terms of digital electronics, we have-
= (p’ + q)’ + (p’ + p.q)
= (p’ + q)’ + (p’ + p).(p’ + q) { Using Transposition theorem }
= (p’ + q)’ + 1.(p’ + q)
= (p’ + q)’ + (p’ + q)
= p.q’ + p’ + q { Using De Morgans law }
= (p + p’)(p’ + q’) + q { Using Transposition theorem }
= 1.(p’ + q’) + q
= p’ + (q’ + q)
= p’ + 1
= 1
- Clearly, the result is 1.
- So, given proposition is a tautology, valid, unfalsifiable and satisfiable.
Part-05:
Method-01: Using Truth Table-
Let (p ↔ r) → (∼q → (p ∧ r)) = R (say)
| p | q | r | ∼q |
p → r | r → p | p ↔ r | p ∧ r | ∼q → (p ∧ r) | R |
| F | F | F | T | T | T | T | F | F | F |
| F | F | T | T | T | F | F | F | F | T |
| F | T | F | F | T | T | T | F | T | T |
| F | T | T | F | T | F | F | F | T | T |
| T | F | F | T | F | T | F | F | F | T |
| T | F | T | T | T | T | T | T | T | T |
| T | T | F | F | F | T | F | F | T | T |
| T | T | T | F | T | T | T | T | T | T |
Clearly, last column of the truth table contains both T and F.
Therefore, given proposition is-
- Contingency
- Invalid
- Falsifiable
- Satisfiable
Method-02: Using Algebra Of Proposition-
We have-
(p ↔ r) → (∼q → (p ∧ r))
= (p ↔ r) → (q ∨ (p ∧ r)) { ∵ p → q = ∼p ∨ q }
= ∼(p ↔ r) ∨ q ∨ (p ∧ r)
= ∼((p → r) ∧ (r → p)) ∨ q ∨ (p ∧ r) { ∵ p ↔ q = (p → q) ∧ q → p) }
= ∼((∼p ∨ r) ∧ (∼r ∨ p)) ∨ q ∨ (p ∧ r) { ∵ p → q = ∼p ∨ q }
= ∼[ ((∼p ∨ r) ∧ ∼r) ∨ ((∼p ∨ r) ∧ p) ] ∨ q ∨ (p ∧ r) { Using Distributive law }
= ∼[ ((∼p ∧ ∼r) ∨ (r ∧ ∼r)) ∨ ((∼p ∧ p) ∨ (r ∧ p)) ] ∨ q ∨ (p ∧ r) { Using Distributive law }
= ∼[ ((∼p ∧ ∼r) ∨ F) ∨ (F ∨ (r ∧ p)) ] ∨ q ∨ (p ∧ r) { Using Complement law }
= ∼[ (∼p ∧ ∼r) ∨ (r ∧ p) ] ∨ q ∨ (p ∧ r) { Using Identity law }
= [∼(∼p ∧ ∼r) ∧ ∼(r ∧ p) ] ∨ q ∨ (p ∧ r) { Using De Morgans law }
= [ (p ∨ r) ∧ (∼r ∨ ∼p) ] ∨ q ∨ (p ∧ r) { Using De Morgans law }
= ((p ∨ r) ∧ ∼r) ∨ ((p ∨ r) ∧ ∼p) ∨ q ∨ (p ∧ r) { Using Distributive law }
= ((p ∧ ∼r) ∨ (r ∧ ∼r)) ∨ ((p ∧ ∼p) ∨ (r ∧ ∼p)) ∨ q ∨ (p ∧ r) { Using Distributive law }
= ((p ∧ ∼r) ∨ F) ∨ (F ∨ (r ∧ ∼p)) ∨ q ∨ (p ∧ r) { Using Complement law }
= (p ∧ ∼r) ∨ (r ∧ ∼p) ∨ q ∨ (p ∧ r) { Using Identity law }
= (p ∧ ∼r) ∨ q ∨ (∼p ∧ r) ∨ (p ∧ r)
= (p ∧ ∼r) ∨ q ∨ ((∼p ∨ p) ∧ r) { Using Distributive law }
= (p ∧ ∼r) ∨ q ∨ (T ∧ r) { Using Complement law }
= (p ∧ ∼r) ∨ q ∨ r { Using Identity law }
= r ∨ (p ∧ ∼r) ∨ q
= ((r ∨ p) ∧ (r ∨ ∼r)) ∨ q { Using Distributive law }
= ((r ∨ p) ∧ T) ∨ q { Using Complement law }
= p ∨ q ∨ r { Using Identity law }
- Clearly, the result is neither T nor F.
- So, given proposition is a contingency, invalid, falsifiable and satisfiable.
Method-03: Using Digital Electronics-
We have-
(p ↔ r) → (∼q → (p ∧ r))
= (p ↔ r) → (q ∨ (p ∧ r)) { ∵ p → q = ∼p ∨ q }
= ∼(p ↔ r) ∨ (q ∨ (p ∧ r)) { ∵ p → q = ∼p ∨ q }
Now in terms of digital electronics, we have-
= (p.r + p’.r’)’ + (q + p.r)
= (p.r)’ . (p’.r’)’ + (q + p.r) (Using De Morgans Theorem)
= (p’ + r’) . (p + r) + (q + p.r) (Using De Morgans Theorem)
= p’.p + p’.r + r’.p + r’.r + q + p.r
= 0 + p’.r + r’.p + 0 + q + p.r
= p’.r + r’.p + q + p.r
= (p’ + p).r + r’.p + q
= r + r’.p + q
= (r + r’).(r + p) + q (Using Transposition Theorem)
= p + q + r
- Clearly, the result is neither 0 nor 1.
- So, given proposition is a contingency, invalid, falsifiable and satisfiable.
To gain better understanding about Tautology, Contradiction and Contingency,
Get more notes and other study material of Propositional Logic.