Propositions-

 

Before you go through this article, make sure that you have gone through the previous article on Propositions.

 

We have discussed-

• Proposition is a declarative statement that is either true or false but not both.
• Connectives are used to combine the propositions.

 

 

In this article, we will discuss about connectives in propositional logic.

 

Logical Connectives-

 

Connectives are the operators that are used to combine one or more propositions.

 

In propositional logic, there are 5 basic connectives-

 

Name of Connective	Connective Word	Symbol
Negation	Not	⌉ or ∼ or ‘ or –
Conjunction	And	∧
Disjunction	Or	∨
Conditional	If-then	→
Biconditional	If and only if	↔

 

1. Negation-

 

If p is a proposition, then negation of p is a proposition which is-

• True when p is false
• False when p is true.

 

Truth Table-

 

p	∼p
F	T
T	F

 

Example-

 

If p : It is raining outside.

Then, Negation of p is-

∼p : It is not raining outside.

 

2. Conjunction-

 

If p and q are two propositions, then conjunction of p and q is a proposition which is-

• True when both p and q are true
• False when both p and q are false

 

Truth Table-

 

p	q	p ∧ q
F	F	F
F	T	F
T	F	F
T	T	T

 

Example-

 

If p and q are two propositions where-

• p : 2 + 4 = 6
• q : It is raining outside.

 

Then, conjunction of p and q is-

p ∧ q : 2 + 4 = 6 and it is raining outside

 

3. Disjunction-

 

If p and q are two propositions, then disjunction of p and q is a proposition which is-

• True when either one of p or q or both are true
• False when both p and q are false

 

Truth Table-

 

p	q	p ∨ q
F	F	F
F	T	T
T	F	T
T	T	T

 

Example-

 

If p and q are two propositions where-

• p : 2 + 4 = 6
• q : It is raining outside

 

Then, disjunction of p and q is-

p ∨ q : 2 + 4 = 6 or it is raining outside

 

4. Conditional-

 

If p and q are two propositions, then-

• Proposition of the type “If p then q” is called a conditional or implication proposition.
• It is true when both p and q are true or when p is false.
• It is false when p is true and q is false.

 

Truth Table-

 

p	q	p → q
F	F	T
F	T	T
T	F	F
T	T	T

 

Examples-

 

• If a = b and b = c then a = c.
• If I will go to Australia, then I will earn more money.

 

5. Biconditional-

 

If p and q are two propositions, then-

• Proposition of the type “p if and only if q” is called a biconditional or bi-implication proposition.
• It is true when either both p and q are true or both p and q are false.
• It is false in all other cases.

 

Truth Table-

 

p	q	p ↔ q
F	F	T
F	T	F
T	F	F
T	T	T

 

Examples-

 

• He goes to play a match if and only if it does not rain.
• Birds fly if and only if sky is clear.

 

Important Notes-

 

Note-01:

 

• Negation ≡ NOT Gate of digital electronics.
• Conjunction ≡ AND Gate of digital electronics.
• Disjunction ≡ OR Gate of digital electronics.
• Biconditional = EX-NOR Gate of digital electronics.

 

Note-02:

 

• Each logical connective has some priority.
• This priority order is important while solving questions.
• The decreasing order of priority is-

 

 

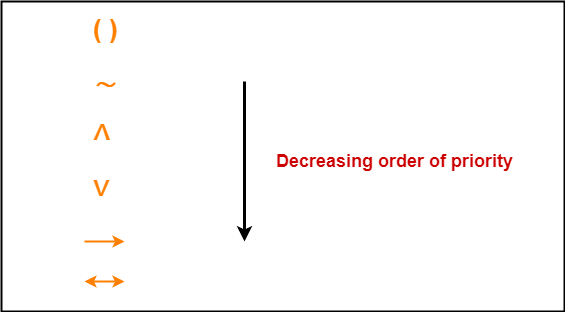
Note-03:

 

• Negation, Conjunction, Disjunction and Biconditional are both commutative and associative.
• Conditional is neither commutative nor associative.

 

To gain better understanding about Logical Connectives,

Watch this Video Lecture

 

Next Article- Converting English Sentences To Propositional Logic

 

Get more notes and other study material of Propositional Logic.