Context Free Language-
Before you go through this article, make sure that you have gone through the previous article on Context Free Language.
We have discussed-
- Context free language is generated using a context free grammar.
- Each context free language is accepted by a Pushdown automaton.
In this article, we will discuss a decision algorithm of CFL.
Algorithm To Decide Whether CFL Is Finite Or Not-
For a given CFG, there exists an algorithm to decide whether its language is finite or not.
Step-01:
Reduce the given grammar completely by-
- Eliminating ∈ productions
- Eliminating unit productions
- Eliminating useless productions
Also Watch- How To Reduce Grammar?
Step-02:
- Draw a directed graph whose nodes are variables of the given grammar.
- There exists an edge from node A to node B if there exists a production of the form A → αBβ.
Now, following 2 cases are possible-
Case-01:
- Directed graph contains a cycle.
- In this case, language of the given grammar is infinite.
Case-02:
- Directed graph does not contain any cycle.
- In this case, language of the given grammar is finite.
Also Read- Algorithm To Decide Whether CFL Is Empty
PRACTICE PROBLEMS BASED ON DECIDING WHETHER CFL IS FINITE-
Problem-01:
Check whether language of the following grammar is finite or not-
S → AB / a
A → BC / b
B → CC / c
Solution-
Step-01:
The given grammar is already completely reduced.
Step-02:
We will draw a directed graph whose nodes will be S , A , B , C.
Now,
- Due to the production S → AB, directed graph will have edges S → A and S → B.
- Due to the production A → BC, directed graph will have edges A → B and A → C.
- Due to the production B → CC, directed graph will have edge B → C.
The required directed graph is-
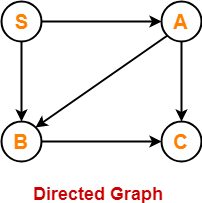
Clearly,
- The directed graph does not contain any cycle.
- Therefore, language of the given grammar is finite.
Problem-02:
Check whether language of the following grammar is finite or not-
S → XS / b
X → YZ
Y → ab
Z → XY
Solution-
Step-01:
The given grammar is already completely reduced.
Step-02:
We will draw a directed graph whose nodes will be S , X , Y , Z.
Now,
- Due to the production S → XS / b, directed graph will have edges S → X and S → S.
- Due to the production X → YZ, directed graph will have edges X → Y and X → Z.
- Due to the production Z → XY, directed graph will have edges Z → X and Z → Y.
The required directed graph is-
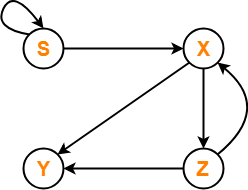
Clearly,
- The directed graph contain cycles.
- Therefore, language of the given grammar is infinite.
Next Article- CYK Algorithm
Get more notes and other study material of Theory of Automata and Computation.
Watch video lectures by visiting our YouTube channel LearnVidFun.