CYK Algorithm | CYK Algorithm Example

CYK Algorithm-

 

CYK Algorithm is a membership algorithm of context free grammar.

 

• It is used to decide whether a given string belongs to the language of grammar or not.
• It is also known as CKY Algorithm or Cocke-Younger-Kasami Algorithm after its inventors.

 

Important Notes-

 

Note-01:

 

• CYK Algorithm operates only on Context Free Grammars given in Chomsky Normal Form.

 

Note-02:

 

• The worst case running time of CYK Algorithm is Θ (n³.|G|).
• Here, n = Length of parsed string and |G| = Size of the CNF Grammar G.

 

Algorithm-

 

Begin
      for ( i = 1 to n do )
      Vi1 { A | A → a is a production where ith symbol of x is a }

      for ( j = 2 to n do )
           for ( i = 1 to n - j + 1 do )
           Begin
                 Vij = ϕ
                 For k = 1 to j - 1 do
                 Vij = Vij ∪ { A | A → BC is a production where B is in Vik and C is in V(i + k)(j - k) }
           End
End

 

Also Read- Algorithm To Check Whether CFL is Empty

 

Deciding Membership Using CYK Algorithm-

 

To decide the membership of any given string, we construct a triangular table where-

• Each row of the table corresponds to one particular length of sub strings.
• Bottom most row corresponds to strings of length-1.
• Second row from bottom corresponds to strings of length-2.
• Third row from bottom corresponds to strings of length-3.
• Top most row from bottom corresponds to the given string of length-n.

 

Example-

 

For a given string “x” of length 4 units, triangular table looks like-

 

 

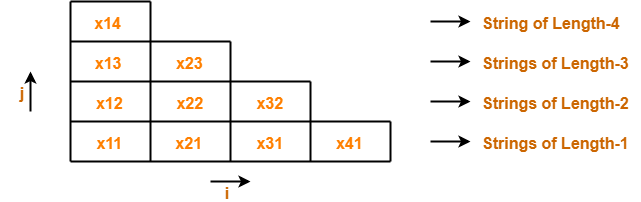
We will fill each box of x_ij with its V_ij.

These notations are discussed below.

 

Notations Used   Notation-01: xij   xij represents a sub string of “x” starting from location ‘i’ and has length ‘j’. Example- Consider x = abcd is a string, then- Number of sub strings possible = n(n+1)/2 = 4 x (4+1) / 2 = 10 We have- x11 = a x21 = b x31 = c x41 = d x12 = ab x22 = bc x32 = cd x13 = abc x23 = bcd x14 = abcd   Notation-02: Vij   Vij represents a set of variables in the grammar which can derive the sub string xij. If the set of variables consists of the start symbol, then it becomes sure- Sub string xij can be derived from the given grammar. Sub string xij is a member of the language of the given grammar.

 

Also Read- Algorithm To Check Whether CFL is Finite

 

PRACTICE PROBLEM BASED ON CYK ALGORITHM-

 

Problem-

 

For the given grammar, check the acceptance of string w = baaba using CYK Algorithm-

S → AB / BC

A → BA / a

B → CC / b

C → AB / a

Solution-

 

First, let us draw the triangular table.

• The given string is x = baaba.
• Length of given string = |x| = 5.
• So, Number of sub strings possible = (5 x 6) / 2 = 15.

 

So, triangular table looks like-

 

 

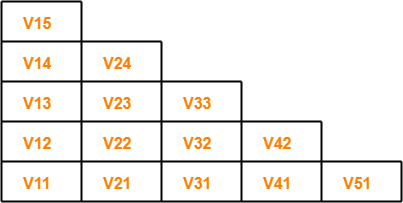
Now, let us find the value of V_ij for each cell.

 

For Row-1:

 

Finding V₁₁

 

• V₁₁ represents the set of variables deriving x₁₁.
• x₁₁ = b.
• Only variable B derives string “b” in the given grammar.
• Thus, V₁₁ = { B }

 

Finding V₂₁

 

• V₂₁ represents the set of variables deriving x₂₁.
• x₂₁ = a.
• Variables A and C derive string “a” in the given grammar.
• Thus, V₂₁ = { A , C }

 

Finding V₃₁

 

• V₃₁ represents the set of variables deriving x₃₁.
• x₃₁ = a.
• Variables A and C derive string “b” in the given grammar.
• Thus, V₃₁ = { A , C }

 

Finding V₄₁

 

• V₄₁ represents the set of variables deriving x₄₁.
• x₄₁ = b.
• Only variable B derives string “b” in the given grammar.
• Thus, V₄₁ = { B }

 

Finding V₅₁

 

• V₅₁ represents the set of variables deriving x₅₁.
• x₅₁ = a.
• Variables A and C derives string “a” in the given grammar.
• Thus, V₅₁ = { A , C }

 

For Row-2-

 

RULE As per the algorithm, to find the value of Vij from 2nd row on wards, we use the formula- Vij = Vik V(i+k)(j-k) where k varies from 1 to j-1

 

Finding V₁₂

 

We have i = 1 , j = 2 , k = 1

Substituting values in the formula, we get-

V₁₂ = V₁₁. V₂₁

V₁₂ = { B } { A , C }

V₁₂ = { BA , BC }

∴ V₁₂ = { A , S }

 

Finding V₂₂

 

We have i = 2 , j = 2 , k = 1

Substituting values in the formula, we get-

V₂₂ = V₂₁. V₃₁

V₂₂ = { A , C } { A , C }

V₂₂ = { AA , AC , CA , CC }

Since AA , AC and CA do not exist, so we have-

V₂₂ = { CC }

∴ V₂₂ = { B }

 

Finding V₃₂

 

We have i = 3 , j = 2 , k = 1

Substituting values in the formula, we get-

V₃₂ = V₃₁. V₄₁

V₃₂ = { A , C } { B }

V₃₂ = { AB , CB }

Since CB does not exist, so we have-

V₃₂ = { AB }

∴ V₃₂ = { S , C }

 

Finding V₄₂

 

We have i = 4 , j = 2 , k = 1

Substituting values in the formula, we get-

V₄₂ = V₄₁. V₅₁

V₄₂ = { B } { A , C }

V₄₂ = { BA , BC }

∴ V₄₂ = { A , S }

 

For Row-3-

 

Finding V₁₃

 

We have i = 1 , j = 3 , k = 1 to (3-1) = 1,2

Substituting values in the formula, we get-

V₁₃ = V₁₁. V₂₂ ∪ V₁₂. V₃₁

V₁₃ = { B } { B } ∪ { A , S } { A , C }

V₁₃ = { BB } ∪ { AA , AC , SA , SC }

Since BB , AA , AC , SA and SC do not exist, so we have-

V₁₃ = ϕ ∪ ϕ

∴ V₁₃ = ϕ

 

Finding V₂₃

 

We have i = 2 , j = 3 , k = 1 to (3-1) = 1,2

Substituting values in the formula, we get-

V₂₃ = V₂₁. V₃₂ ∪ V₂₂. V₄₁

V₂₃ = { A , C } { S , C } ∪ { B } { B }

V₂₃ = { AS , AC , CS , CC } ∪ { BB }

Since AS , AC , CS and BB do not exist, so we have-

V₂₃ = { CC }

∴ V₂₃ = B

 

Finding V₃₃

 

We have i = 3 , j = 3 , k = 1 to (3-1) = 1,2

Substituting values in the formula, we get-

V₃₃ = V₃₁. V₄₂ ∪ V₃₂. V₅₁

V₃₃ = { A , C } { A , S } ∪ { S , C } { A , C }

V₃₃ = { AA , AS , CA , CS } ∪ { SA , SC , CA , CC }

Since AA , AS , CA , CS , SA , SC and CA do not exist, so we have-

V₃₃ = ϕ ∪ { CC }

V₃₃ = ϕ ∪ { B }

∴ V₃₃ = { B }

 

For Row-4-

 

Finding V₁₄

 

We have i = 1 , j = 4 , k = 1 to (4-1) = 1,2,3

Substituting values in the formula, we get-

V₁₄ = V₁₁. V₂₃ ∪ V₁₂. V₃₂ ∪ V₁₃. V₄₁

V₁₄ = { B } { B } ∪ { A , S } { S , C } ∪ { ϕ , B }

V₁₄ = { BB } ∪ { AS , AC , SS , SC } ∪ { B }

Since BB , AS , AC , SS , SC and B do not exist, so we have-

V₁₄ = ϕ ∪ ϕ ∪ ϕ

∴ V₁₄ = ϕ

 

Finding V₂₄

 

We have i = 2 , j = 4 , k = 1 to (4-1) = 1,2,3

Substituting values in the formula, we get-

V₂₄ = V₂₁. V₃₃ ∪ V₂₂. V₄₂ ∪ V₂₃. V₅₁

V₂₄ = { A , C } { B } ∪ { B } { A , S } ∪ { B } { A , C }

V₂₄ = { AB , CB } ∪ { BA , BS } ∪ { BA , BC }

Since CB does not exist, so we have-

V₂₄ = { AB } ∪ { BA , BS } ∪ { BA , BC }

V₂₄ = { S , C } ∪ { A } ∪ { A , S }

∴ V₂₄ = { S , C , A }

 

For Row-5-

 

Finding V₁₅

 

We have i = 1 , j = 5 , k = 1 to (5-1) = 1,2,3,4

Substituting values in the formula, we get-

V₁₅ = V₁₁. V₂₄ ∪ V₁₂. V₃₃ ∪ V₁₃. V₄₂ ∪ V₁₄. V₅₁

V₁₅ = { B } { S , C , A } ∪ { A , S } { B } ∪ { ϕ } { A , S } ∪ { ϕ } { A , C }

V₁₅ = { BS , BC , BA } ∪ { AB , SB } ∪ { A , S } ∪ { A , C }

Since BS , SB , A , S and C do not exist, so we have-

V₁₅ = { BC , BA } ∪ { AB } ∪ ϕ ∪ ϕ

V₁₅ = { S , A } ∪ { S , C } ∪ ϕ ∪ ϕ

∴ V₁₅ = { S , A , C }

 

Now,

• The value of V_ij is computed for each cell.
• We observe V₁₅ contains the start symbol S.
• Thus, string x₁₅ = baaba is a member of the language of given grammar.

 

After filling the triangular table, it looks like-

 

 

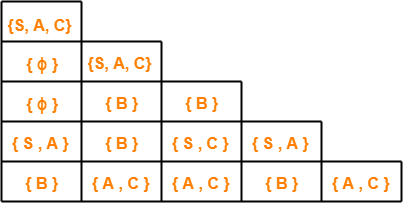
Results From Triangular Table-

 

The following important results can be made from the above triangular table-

 

Result-01:

 

• There exists total 4 distinct sub strings which are members of the language of given grammar.
• These 4 sub strings are ba, ab, aaba, baaba.
• This is because they contain start symbol in their respective cell.

 

Result-02:

 

• Strings which can not be derived from any variable are baa, baab.
• This is because they contain ϕ in their respective cell.

 

Result-03:

 

• Strings which can be derived from variable B alone are b, aa, aba, aab.
• This is because they contain variable B alone in their respective cell.

 

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.