Evaluating Expressions Based On Given Grammar-
There are two methods for evaluating the expressions based on given grammar-
- Drawing a parse tree
- Designing the rules for operators
Method-01: Drawing Parse Tree-
In this method, following steps are followed-
- We draw a Parse Tree for the given expression.
- We evaluate the parse tree to get the required value of the expression.
Drawback-
- Drawing a parse tree for large expressions is cumbersome and time taking.
- So, this method becomes difficult to follow when the expression is large.
Method-02: Designing Rules For Operators-
In this method, following steps are followed-
- We decide the priority and associativity of operators in the grammar.
- We parenthesize the given expression.
- We evaluate the expression to get the required value.
Advantage-
- This method is easy to follow whether the expression is small or large.
- So, this method is preferred.
Rules For Deciding Priority Of Operators-
For the given unambiguous grammar,
- The priority of operators is decided by checking the level at which the production is present.
- The higher the level of production, the lower the priority of operator contained in it.
- The lower the level of production, the higher the priority of operator contained in it.
Also Read- Converting Ambiguous into Unambiguous Grammar
Example-
Consider the grammar-
E → E x F / F + E / F
F → F – T / T
T → id
Here,
- id has the highest priority.
(since T → id is present at the bottom most level)
- x and + operators have the least priority.
(since E → E x F / F + E are present at the top most level)
- x and + operators have the same priority.
(since E → E x F / F + E are present at the same level)
- – operator has higher priority than x and + but lesser priority than id.
(since F → F – T is present at the middle level)
So, the priority order is-
id > – > ( x , + )
Rules For Deciding Associativity Of Operators-
For the given unambiguous grammar,
- The associativity of operators is decided by checking the Type Of Recursion in the production.
- If the production has left recursion, then the operator is left associative.
- If the production has right recursion, then the operator is right associative.
- If the production has both left and right recursion, then the operator is neither left associative nor right associative.
Example-
Consider the grammar-
E → E x F / F + E / F
F → F – F / T
T → id
Here,
- x operator is left associative.
(since E → E x F has left recursion in it)
- + operator is right associative.
(since E → F + E has right recursion in it)
- F – F is neither left associative nor right associative.
(since F → F – F has both left and right recursion in it)
PRACTICE PROBLEMS BASED ON EVALUATING EXPRESSIONS FOR GRAMMAR-
Problem-01:
Consider the given grammar-
E → E + T / T
T → F x T / F
F → id
Evaluate the following expression in accordance with the given grammar-
2 + 3 x 5 x 6 + 2
Solution-
Method-01:
- Let us draw a parse tree for the given expression.
- Evaluating the parse tree will return the required value of the expression.
The parse tree for the given expression is-
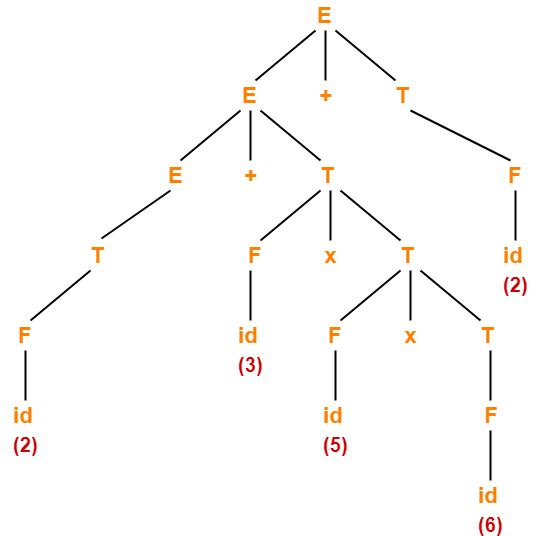
On evaluating this parse tree, we get the value = 94.
Method-02:
The priority order and associativity of operators on the basis of given grammar is-
id > x > +
where-
- x operator is right associative.
- + operator is left associative.
Now, we parenthesize the given expression based on the precedence and associativity of operators as-
( 2 + ( 3 x ( 5 x 6 ) ) ) + 2
Now, we evaluate the parenthesized expression as-
= ( 2 + ( 3 x ( 5 x 6 ) ) ) + 2
= ( 2 + ( 3 x 30 ) ) + 2
= ( 2 + 90 ) + 2
= 92 + 2
= 94
Problem-02:
Consider the given grammar-
E → E + T / E – T / T
T → T x F / T ÷ F / F
F → G ↑ F / G
G → id
Evaluate the following expression in accordance with the given grammar-
2 x 1 + 4 ↑ 2 ↑ 1 x 1 + 3
Solution-
Method-01:
- Let us draw a parse tree for the given expression.
- Evaluating the parse tree will return the required value of the expression.
The parse tree for the given expression is-
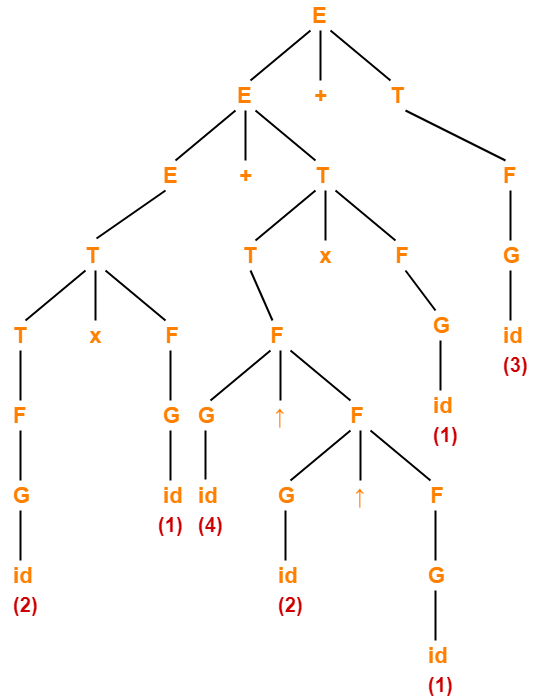
On evaluating this parse tree, we get the value = 21.
Method-02:
The priority order and associativity of operators on the basis of given grammar is-
id > ↑ > ( x , ÷ ) > ( + , – )
where-
- + , – , x , ÷ operators are left associative.
- ↑ operator is right associative
Now, we parenthesize the given expression based on the precedence and associativity of operators as-
( ( 2 x 1 ) + ( ( 4 ↑ ( 2 ↑ 1 ) ) x 1 ) ) + 3
Now, we evaluate the parenthesized expression as-
= ( ( 2 x 1 ) + ( ( 4 ↑ ( 2 ↑ 1 ) ) x 1 ) ) + 3
= ( ( 2 x 1 ) + ( ( 4 ↑ 2 ) x 1 ) ) + 3
= ( ( 2 x 1 ) + ( 16 x 1 ) ) + 3
= ( 2 + ( 16 x 1 ) ) + 3
= ( 2 + 16 ) + 3
= 18 + 3
= 21
Problem-03:
Consider the given grammar-
E → E + T / E – T / T
T → T x F / T ÷ F / F
F → F ↑ G / G
G → id
Evaluate the following expression in accordance with the given grammar-
2 ↑ 1 ↑ 4 + 3 x 5 x 6 ↑ 1 + 2 ↑ 3
Solution-
The priority order and associativity of operators on the basis of given grammar is-
id > ↑ > ( x , ÷ ) > ( + , – )
where + , – , x , ÷, ↑ operators are left associative.
Now, we parenthesize the given expression based on the precedence and associativity of operators as-
( ( ( 2 ↑ 1 ) ↑ 4 ) + ( ( 3 x 5 ) x ( 6 ↑ 1 ) ) ) + ( 2 ↑ 3 )
Now, we evaluate the parenthesized expression as-
= ( ( ( 2 ↑ 1 ) ↑ 4 ) + ( ( 3 x 5 ) x ( 6 ↑ 1 ) ) ) + ( 2 ↑ 3 )
= ( ( 2 ↑ 4 ) + ( ( 3 x 5 ) x ( 6 ↑ 1 ) ) ) + ( 2 ↑ 3 )
= ( 16 + ( ( 3 x 5 ) x ( 6 ↑ 1 ) ) ) + ( 2 ↑ 3 )
= ( 16 + ( ( 3 x 5 ) x 6 ) ) + ( 2 ↑ 3 )
= ( 16 + ( ( 3 x 5 ) x 6 ) ) + 8
= ( 16 + ( 15 x 6 ) ) + 8
= ( 16 + 90 ) + 8
= 106 + 8
= 114
Problem-04:
Consider the given grammar-
E → E ↑ T / T
T → T + F / F
F → G – F / G
G → id
Evaluate the following expression in accordance with the given grammar-
2 ↑ 1 ↑ 3 + 5 – 6 – 8 – 5 + 10 + 11 ↑ 2
Solution-
The priority order and associativity of operators on the basis of given grammar is-
id > – > + > ↑
where-
- + , ↑ operators are left associative.
- – is right associative.
Now, we parenthesize the given expression based on the precedence and associativity of operators as-
( ( 2 ↑ 1 ) ↑ ( ( ( 3 + ( 5 – ( 6 – ( 8 – 5 ) ) ) ) + 10 ) + 11 ) ) ↑ 2
Now, we evaluate the parenthesized expression as-
= ( ( 2 ↑ 1 ) ↑ ( ( ( 3 + ( 5 – ( 6 – ( 8 – 5 ) ) ) ) + 10 ) + 11 ) ) ↑ 2
= ( ( 2 ↑ 1 ) ↑ ( ( ( 3 + ( 5 – ( 6 – 3 ) ) ) + 10 ) + 11 ) ) ↑ 2
= ( ( 2 ↑ 1 ) ↑ ( ( ( 3 + ( 5 – 3 ) ) + 10 ) + 11 ) ) ↑ 2
= ( ( 2 ↑ 1 ) ↑ ( ( ( 3 + 2 ) + 10 ) + 11 ) ) ↑ 2
= ( ( 2 ↑ 1 ) ↑ ( ( 5 + 10 ) + 11 ) ) ↑ 2
= ( ( 2 ↑ 1 ) ↑ ( 15 + 11 ) ) ↑ 2
= ( ( 2 ↑ 1 ) ↑ 26 ) ↑ 2
= ( 2 ↑ 26 ) ↑ 2
= (226) ↑ 2
= (226)2
Problem-05:
Consider the given priority order of operators-
id > ( x , ÷ ) > ( + , – )
Given all the operators are left associative, construct the corresponding grammar.
Solution-
We apply the rules learnt above in reverse direction to obtain the required grammar.
The corresponding grammar is-
E → E + T / E – T / T
T → T x F / T ÷ F / F
F → id
Problem-06:
Consider the given priority order of operators-
id > ↑ > ( x , ÷ ) > ( + , – )
Given all the operators are left associative, construct the corresponding grammar.
Solution-
The corresponding grammar is-
E → E + T / E – T / T
T → T x F / T ÷ F / F
F → G ↑ F / G
G → id
Next Article- Important Points For Exams
Get more notes and other study material of Theory of Automata and Computation.
Watch video lectures by visiting our YouTube channel LearnVidFun.