Tag: DDA Line Drawing Algorithm

DDA Algorithm | Line Drawing Algorithms

Computer Graphics

Line Drawing Algorithms-

 

In computer graphics, popular algorithms used to generate lines are-

 

 

  1. Digital Differential Analyzer (DDA) Line Drawing Algorithm
  2. Bresenham Line Drawing Algorithm
  3. Mid Point Line Drawing Algorithm

 

In this article, we will discuss about DDA Algorithm.

 

DDA Algorithm-

 

DDA Algorithm is the simplest line drawing algorithm.

 

Given the starting and ending coordinates of a line,

DDA Algorithm attempts to generate the points between the starting and ending coordinates.

 

Procedure-

 

Given-

  • Starting coordinates = (X0, Y0)
  • Ending coordinates = (Xn, Yn)

 

The points generation using DDA Algorithm involves the following steps-

 

Step-01:

 

Calculate ΔX, ΔY and M from the given input.

These parameters are calculated as-

  • ΔX = Xn – X0
  • ΔY =Yn – Y0
  • M = ΔY / ΔX

 

Step-02:

 

Find the number of steps or points in between the starting and ending coordinates.

 

if (absolute (ΔX) > absolute (ΔY))

Steps = absolute (ΔX);

else

Steps = absolute (ΔY);

 

Step-03:

 

Suppose the current point is (Xp, Yp) and the next point is (Xp+1, Yp+1).

Find the next point by following the below three cases-

 

 

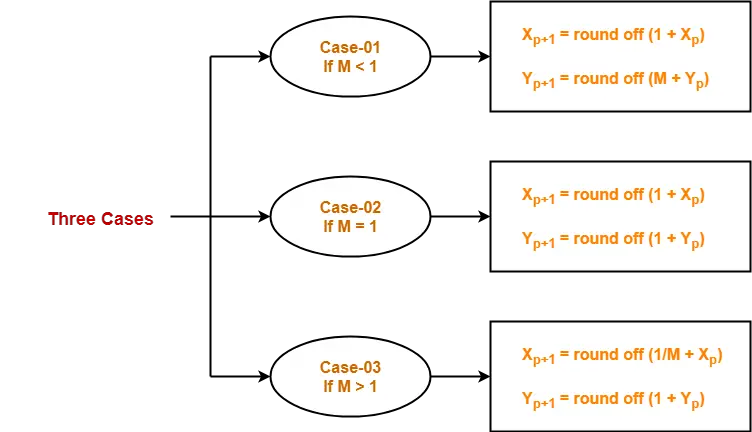
Step-04:

 

Keep repeating Step-03 until the end point is reached or the number of generated new points (including the starting and ending points) equals to the steps count.

 

PRACTICE PROBLEMS BASED ON DDA ALGORITHM-

 

Problem-01:

 

Calculate the points between the starting point (5, 6) and ending point (8, 12).

 

Solution-

 

Given-

  • Starting coordinates = (X0, Y0) = (5, 6)
  • Ending coordinates = (Xn, Yn) = (8, 12)

 

Step-01:

 

Calculate ΔX, ΔY and M from the given input.

  • ΔX = Xn – X0 = 8 – 5 = 3
  • ΔY =Yn – Y0 = 12 – 6 = 6
  • M = ΔY / ΔX = 6 / 3 = 2

 

Step-02:

 

Calculate the number of steps.

As |ΔX| < |ΔY| = 3 < 6, so number of steps = ΔY = 6

 

Step-03:

 

As M > 1, so case-03 is satisfied.

Now, Step-03 is executed until Step-04 is satisfied.

 

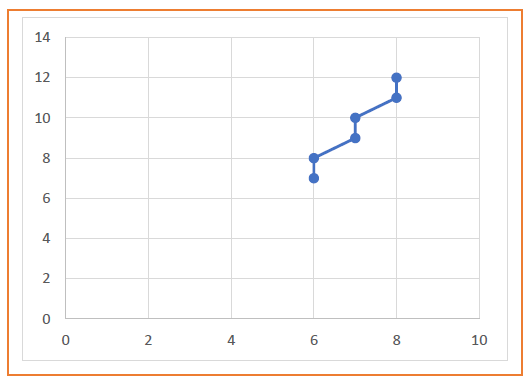
Xp Yp Xp+1 Yp+1 Round off (Xp+1, Yp+1)
5 6 5.5 7 (6, 7)
6 8 (6, 8)
6.5 9 (7, 9)
7 10 (7, 10)
7.5 11 (8, 11)
8 12 (8, 12)

 

 

Problem-02:

 

Calculate the points between the starting point (5, 6) and ending point (13, 10).

 

Solution-

 

Given-

  • Starting coordinates = (X0, Y0) = (5, 6)
  • Ending coordinates = (Xn, Yn) = (13, 10)

 

Step-01:

 

Calculate ΔX, ΔY and M from the given input.

  • ΔX = Xn – X0 = 13 – 5 = 8
  • ΔY =Yn – Y0 = 10 – 6 = 4
  • M = ΔY / ΔX = 4 / 8 = 0.50

 

Step-02:

 

Calculate the number of steps.

As |ΔX| > |ΔY| = 8 > 4, so number of steps = ΔX = 8

 

Step-03:

 

As M < 1, so case-01 is satisfied.

Now, Step-03 is executed until Step-04 is satisfied.

 

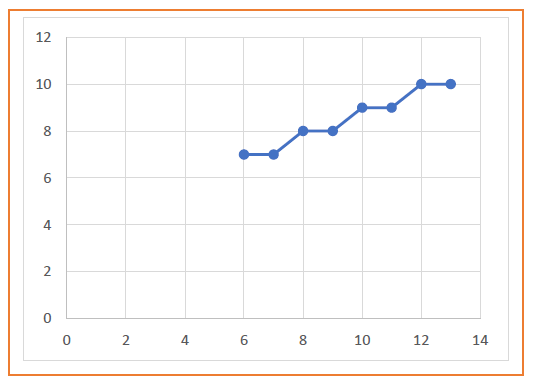
Xp Yp Xp+1 Yp+1 Round off (Xp+1, Yp+1)
5 6 6 6.5 (6, 7)
7 7 (7, 7)
8 7.5 (8, 8)
9 8 (9, 8)
10 8.5 (10, 9)
11 9 (11, 9)
12 9.5 (12, 10)
13 10 (13, 10)

 

 

Problem-03:

 

Calculate the points between the starting point (1, 7) and ending point (11, 17).

 

Solution-

 

Given-

  • Starting coordinates = (X0, Y0) = (1, 7)
  • Ending coordinates = (Xn, Yn) = (11, 17)

 

Step-01:

 

Calculate ΔX, ΔY and M from the given input.

  • ΔX = Xn – X0 = 11 – 1 = 10
  • ΔY =Yn – Y0 = 17 – 7 = 10
  • M = ΔY / ΔX = 10 / 10 = 1

 

Step-02:

 

Calculate the number of steps.

As |ΔX| = |ΔY| = 10 = 10, so number of steps = ΔX = ΔY = 10

 

Step-03:

 

As M = 1, so case-02 is satisfied.

Now, Step-03 is executed until Step-04 is satisfied.

 

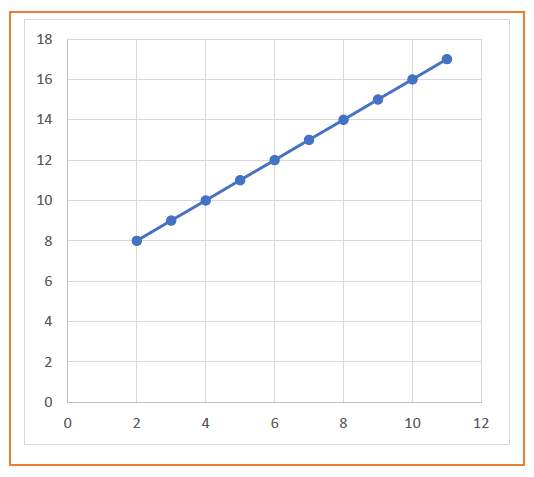
Xp Yp Xp+1 Yp+1 Round off (Xp+1, Yp+1)
1 7 2 8 (2, 8)
3 9 (3, 9)
4 10 (4, 10)
5 11 (5, 11)
6 12 (6, 12)
7 13 (7, 13)
8 14 (8, 14)
9 15 (9, 15)
10 16 (10, 16)
11 17 (11, 17)

 

 

Advantages of DDA Algorithm-

 

The advantages of DDA Algorithm are-

  • It is a simple algorithm.
  • It is easy to implement.
  • It avoids using the multiplication operation which is costly in terms of time complexity.

 

Disadvantages of DDA Algorithm-

 

The disadvantages of DDA Algorithm are-

  • There is an extra overhead of using round off( ) function.
  • Using round off( ) function increases time complexity of the algorithm.
  • Resulted lines are not smooth because of round off( ) function.
  • The points generated by this algorithm are not accurate.

 

To gain better understanding about DDA Algorithm,

Watch this Video Lecture

 

Next Article- Bresenham Line Drawing Algorithm

 

Get more notes and other study material of Computer Graphics.

Watch video lectures by visiting our YouTube channel LearnVidFun.