Language Of Grammar-
Before you go through this article, make sure that you have gone through the previous article on Language of Grammar.
We have discussed-
- Language of grammar is the set of all strings that can be generated from that grammar.
- Finite language consists of finite number of strings.
- Infinite language consists of infinite number of strings.
In this article, we will discuss about Language Ambiguity.
Language Ambiguity-
| If every grammar that generates language L is ambiguous,
then language L is called as Inherently ambiguous language. OR A language is inherently ambiguous if all the grammars which generate that language are ambiguous. |
Also Read- Ambiguous Grammar
NOTE-
- The term “inherently ambiguous language” is used instead of “ambiguous language”.
- This is because all the grammars which generate that language are ambiguous.
Important Points-
- If a grammar is ambiguous, it does not imply that its language will be ambiguous too.
- If a grammar is ambiguous, its language may be unambiguous.
- If a grammar is ambiguous, its language will be unambiguous when there exists at least one unambiguous grammar which generates that language.
Example Of Not An Inherently Ambiguous Language-
Consider the following language-
L = an , n>=0
- This language consists of strings having any number of a’s.
- Few grammars which generate this language are-
Grammar-01:
S → aS / ∈
(Unambiguous Grammar)
Grammar-02:
S → aS / a / ∈
(Ambiguous Grammar)
Grammar-03:
S → aS / Sa / ∈
(Ambiguous Grammar)
Grammar-04:
S → aS / a / Sa / ∈
(Ambiguous Grammar)
- All the above grammars generate the same language L = an , n>=0.
- Grammar-01 is unambiguous.
- Since there exists at least one unambiguous grammar which generates language L.
- Therefore, L is not an inherently ambiguous language.
Example Of An Inherently Ambiguous Language-
Consider the following language-
L = { anbncm } ∪ { anbmcm }
There exists only one grammar which generates this language L.
The grammar is-
S → S1 / S2
S1 → S1C / A
A → aAb / ∈
S2 → aS2 / B
B → bBc / ∈
This grammar is ambiguous in nature.
This is because following two parse trees exist for string w = abc-
Also Read- Checking Grammar Ambiguity
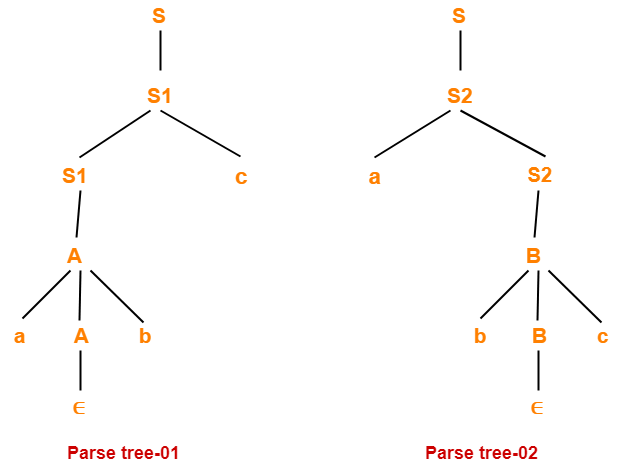
- There exists no language that generates this language L and is unambiguous.
- Therefore, L is an inherently ambiguous language.
Next Article- Context Free Grammar
Get more notes and other study material of Theory of Automata and Computation.
Watch video lectures by visiting our YouTube channel LearnVidFun.