Grammar in Automata-
Formal Definition-
A Grammar is a 4-tuple such that-
G = (V , T , P , S)
where-
- V = Finite non-empty set of non-terminal symbols
- T = Finite set of terminal symbols
- P = Finite non-empty set of production rules
- S = Start symbol
Grammar Constituents-
A Grammar is mainly composed of two basic elements-
1. Terminal symbols
2. Non-terminal symbols
1. Terminal Symbols-
- Terminal symbols are those which are the constituents of the sentence generated using a grammar.
- Terminal symbols are denoted by using small case letters such as a, b, c etc.
2. Non-Terminal Symbols-
- Non-Terminal symbols are those which take part in the generation of the sentence but are not part of it.
- Non-Terminal symbols are also called as auxiliary symbols or variables.
- Non-Terminal symbols are denoted by using capital letters such as A, B, C etc.
Examples of Grammar-
Example-01:
Consider a grammar G = (V , T , P , S) where-
- V = { S } // Set of Non-Terminal symbols
- T = { a , b } // Set of Terminal symbols
- P = { S → aSbS , S → bSaS , S → ∈ } // Set of production rules
- S = { S } // Start symbol
This grammar generates the strings having equal number of a’s and b’s
Example-02:
Consider a grammar G = (V , T , P , S) where-
- V = { S , A , B } // Set of Non-Terminal symbols
- T = { a , b } // Set of Terminal symbols
- P = { S → ABa , A → BB , B → ab , AA → b } // Set of production rules
- S = { S } // Start symbol
Types of Grammars-
Grammars are classified on different basis as-
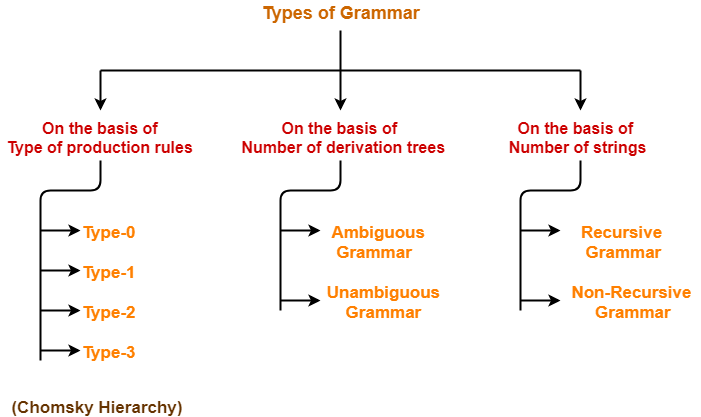
We will discuss all these types of grammar one by one in detail.
Equivalent Grammars-
| Two grammars are said to be equivalent if they generate the same languages. |
Also Read- Language of Grammar
Example-
Consider the following two grammars-
Grammar G1-
S → aSb / ∈
Grammar G2-
S → aAb / ∈
A → aAb / ∈
Both these grammars generate the same language given as-
L = { anbn , n>=0 }
Thus, L(G1) = L(G2)
Since both the grammars generate the same language, therefore they are equivalent.
| ∴ G1 ≡ G2 |
To gain better understanding about Grammars in Automata,
Next Article- Ambiguous Grammar
Get more notes and other study material of Theory of Automata and Computation.
Watch video lectures by visiting our YouTube channel LearnVidFun.

