Binary Tree-
Before you go through this article, make sure that you gone through the previous article on Binary Trees.
We have discussed-
- Binary tree is a special tree data structure.
- In a binary tree, each node can have at most 2 children.
- There are following types of binary trees-

In this article, we will discuss properties of binary trees.
Binary Tree Properties-
Important properties of binary trees are-
Property-01:
|
Minimum number of nodes in a binary tree of height H
= H + 1 |
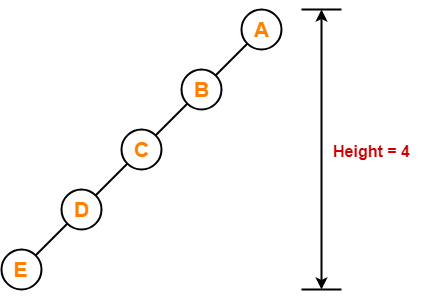
Example-
To construct a binary tree of height = 4, we need at least 4 + 1 = 5 nodes.
Property-02:
|
Maximum number of nodes in a binary tree of height H
= 2H+1 – 1 |
Example-
Maximum number of nodes in a binary tree of height 3
= 23+1 – 1
= 16 – 1
= 15 nodes
Thus, in a binary tree of height = 3, maximum number of nodes that can be inserted = 15.
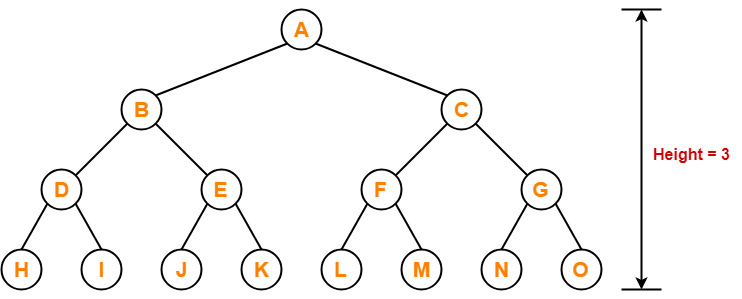
We can not insert more number of nodes in this binary tree.
Property-03:
|
Total Number of leaf nodes in a Binary Tree
= Total Number of nodes with 2 children + 1 |
Example-
Consider the following binary tree-
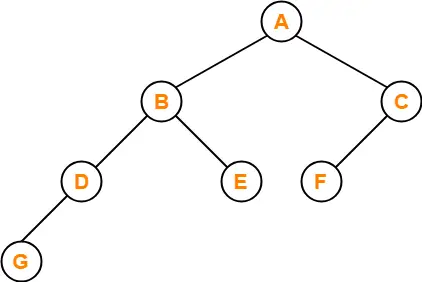
Here,
- Number of leaf nodes = 3
- Number of nodes with 2 children = 2
Clearly, number of leaf nodes is one greater than number of nodes with 2 children.
This verifies the above relation.
NOTEIt is interesting to note that- Number of leaf nodes in any binary tree depends only on the number of nodes with 2 children. |
Property-04:
|
Maximum number of nodes at any level ‘L’ in a binary tree
= 2L |
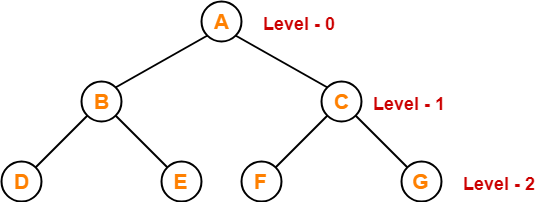
Example-
Maximum number of nodes at level-2 in a binary tree
= 22
= 4
Thus, in a binary tree, maximum number of nodes that can be present at level-2 = 4.
To gain better understanding about Binary Tree Properties,
PRACTICE PROBLEMS BASED ON BINARY TREE PROPERTIES-
Problem-01:
A binary tree T has n leaf nodes. The number of nodes of degree-2 in T is ______?
- log2n
- n-1
- n
- 2n
Solution-
Using property-3, we have-
Number of degree-2 nodes
= Number of leaf nodes – 1
= n – 1
Thus, Option (B) is correct.
Problem-02:
In a binary tree, for every node the difference between the number of nodes in the left and right subtrees is at most 2. If the height of the tree is h > 0, then the minimum number of nodes in the tree is ______?
- 2h-1
- 2h-1 + 1
- 2h – 1
- 2h
Solution-
Let us assume any random value of h. Let h = 3.
Then the given options reduce to-
- 4
- 5
- 7
- 8
Now, consider the following binary tree with height h = 3-
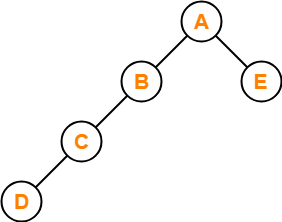
- This binary tree satisfies the question constraints.
- It is constructed using minimum number of nodes.
Thus, Option (B) is correct.
Problem-03:
In a binary tree, the number of internal nodes of degree-1 is 5 and the number of internal nodes of degree-2 is 10. The number of leaf nodes in the binary tree is ______?
- 10
- 11
- 12
- 15
Solution-
Using property-3, we have-
Number of leaf nodes in a binary tree
= Number of degree-2 nodes + 1
= 10 + 1
= 11
Thus, Option (B) is correct.
Problem-04:
The height of a binary tree is the maximum number of edges in any root to leaf path. The maximum number of nodes in a binary tree of height h is ______?
- 2h
- 2h-1 – 1
- 2h+1 – 1
- 2h+1
Solution-
Using property-2, Option (C) is correct.
Problem-05:
A binary tree T has 20 leaves. The number of nodes in T having 2 children is ______?
Solution-
Using property-3, correct answer is 19.
To watch video solutions and practice more problems,
Download Handwritten Notes Here-
Next Article- Binary Tree Traversal
Get more notes and other study material of Data Structures.
Watch video lectures by visiting our YouTube channel LearnVidFun.
