Tag: Konigsberg Bridges

Konigsberg Bridge Problem in Graph Theory

Graph Theory

Konigsberg-

 

  • Konigsberg is the former name of a German city that is now in Russia.
  • The following picture shows the inner city of Konigsberg with the river Pregel.
  • The river Pregel divides the city into four land areas A, B, C and D.
  • In order to travel from one part of the city to another, there exists seven bridges.

 

 

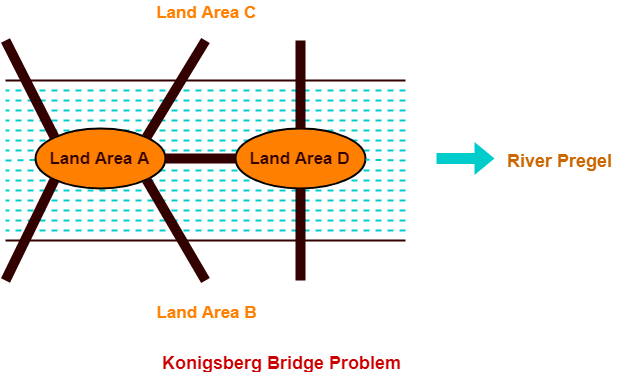
Konigsberg Bridge Problem-

 

Konigsberg Bridge Problem may be stated as-

 

“Starting from any of the four land areas A, B, C, D, is it possible to cross each of the seven bridges

exactly once and come back to the starting point without swimming across the river?”

 

Konigsberg Bridge Problem Solution-

 

In 1735,

  • A Swiss Mathematician Leon hard Euler solved this problem.
  • He provided a solution to the problem and finally concluded that such a walk is not possible.

 

Euler represented the given situation using a graph as shown below-

 

 

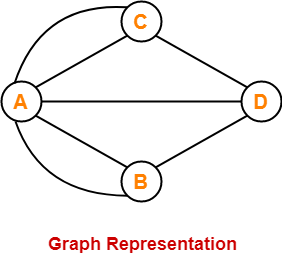
In this graph,

  • Vertices represent the landmasses.
  • Edges represent the bridges.

 

Euler observed that when a vertex is visited during the process of tracing a graph,

  • There must be one edge that enters into the vertex.
  • There must be another edge that leaves the vertex.
  • Therefore, order of the vertex must be an even number.

 

Based on this observation, Euler discovered that it depends on the number of odd vertices present in the network whether any network is traversable or not.

 

Euler found that only those networks are traversable that have either-

  • No odd vertices (then any vertex may be the beginning and the same vertex will also be the ending point)
  • Or exactly two odd vertices (then one odd vertex will be the starting point and other odd vertex will be the ending point)

 

Now,

  • Since the Konigsberg network has four odd vertices, therefore the network is not traversable.
  • Thus, It was finally concluded that the desired walking tour of Konigsberg is not possible.

 

NOTE

If the citizens of Konigsberg decides to build an eighth bridge from A to C, then-

  • It would be possible to walk without traversing any bridge twice.
  • This is because then there will be exactly two odd vertices.

However, adding a ninth bridge will again make the walking tour once again impossible.

 

To gain better understanding about Konigsberg Bridge Problem,

Watch this Video Lecture

 

Next Article- Handshaking Theorem

 

Get more notes and other study material of Graph Theory.

Watch video lectures by visiting our YouTube channel LearnVidFun.