Grammar With Common Prefixes-
| If RHS of more than one production starts with the same symbol,
then such a grammar is called as Grammar With Common Prefixes. |
Example-
A → αβ1 / αβ2 / αβ3
(Grammar with common prefixes)
- This kind of grammar creates a problematic situation for Top down parsers.
- Top down parsers can not decide which production must be chosen to parse the string in hand.
To remove this confusion, we use left factoring.
Left Factoring-
| Left factoring is a process by which the grammar with common prefixes is transformed
to make it useful for Top down parsers. |
How?
In left factoring,
- We make one production for each common prefixes.
- The common prefix may be a terminal or a non-terminal or a combination of both.
- Rest of the derivation is added by new productions.
The grammar obtained after the process of left factoring is called as Left Factored Grammar.
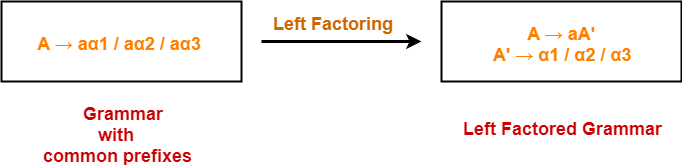
Example-
Also Read- Left Recursion
PRACTICE PROBLEMS BASED ON LEFT FACTORING-
Problem-01:
Do left factoring in the following grammar-
S → iEtS / iEtSeS / a
E → b
Solution-
The left factored grammar is-
S → iEtSS’ / a
S’ → eS / ∈
E → b
Problem-02:
Do left factoring in the following grammar-
A → aAB / aBc / aAc
Solution-
Step-01:
A → aA’
A’ → AB / Bc / Ac
Again, this is a grammar with common prefixes.
Step-02:
A → aA’
A’ → AD / Bc
D → B / c
This is a left factored grammar.
Problem-03:
Do left factoring in the following grammar-
S → bSSaaS / bSSaSb / bSb / a
Solution-
Step-01:
S → bSS’ / a
S’ → SaaS / SaSb / b
Again, this is a grammar with common prefixes.
Step-02:
S → bSS’ / a
S’ → SaA / b
A → aS / Sb
This is a left factored grammar.
Problem-04:
Do left factoring in the following grammar-
S → aSSbS / aSaSb / abb / b
Solution-
Step-01:
S → aS’ / b
S’ → SSbS / SaSb / bb
Again, this is a grammar with common prefixes.
Step-02:
S → aS’ / b
S’ → SA / bb
A → SbS / aSb
This is a left factored grammar.
Problem-05:
Do left factoring in the following grammar-
S → a / ab / abc / abcd
Solution-
Step-01:
S → aS’
S’ → b / bc / bcd / ∈
Again, this is a grammar with common prefixes.
Step-02:
S → aS’
S’ → bA / ∈
A → c / cd / ∈
Again, this is a grammar with common prefixes.
Step-03:
S → aS’
S’ → bA / ∈
A → cB / ∈
B → d / ∈
This is a left factored grammar.
Problem-06:
Do left factoring in the following grammar-
S → aAd / aB
A → a / ab
B → ccd / ddc
Solution-
The left factored grammar is-
S → aS’
S’ → Ad / B
A → aA’
A’ → b / ∈
B → ccd / ddc
To gain better understanding about Left Factoring,
Next Article- Relationship With Left Recursion
Get more notes and other study material of Compiler Design.
Watch video lectures by visiting our YouTube channel LearnVidFun.