Operator Precedence Grammar-
A grammar that satisfies the following 2 conditions is called as Operator Precedence Grammar–
|
- It represents a small class of grammar.
- But it is an important class because of its widespread applications.
Examples-

Operator Precedence Parser-
| A parser that reads and understand an operator precedence grammar
is called as Operator Precedence Parser. |
Designing Operator Precedence Parser-
In operator precedence parsing,
- Firstly, we define precedence relations between every pair of terminal symbols.
- Secondly, we construct an operator precedence table.
Defining Precedence Relations-
The precedence relations are defined using the following rules-
Rule-01:
- If precedence of b is higher than precedence of a, then we define a < b
- If precedence of b is same as precedence of a, then we define a = b
- If precedence of b is lower than precedence of a, then we define a > b
Rule-02:
- An identifier is always given the higher precedence than any other symbol.
- $ symbol is always given the lowest precedence.
Rule-03:
- If two operators have the same precedence, then we go by checking their associativity.
Parsing A Given String-
The given input string is parsed using the following steps-
Step-01:
Insert the following-
- $ symbol at the beginning and ending of the input string.
- Precedence operator between every two symbols of the string by referring the operator precedence table.
Step-02:
- Start scanning the string from LHS in the forward direction until > symbol is encountered.
- Keep a pointer on that location.
Step-03:
- Start scanning the string from RHS in the backward direction until < symbol is encountered.
- Keep a pointer on that location.
Step-04:
- Everything that lies in the middle of < and > forms the handle.
- Replace the handle with the head of the respective production.
Step-05:
Keep repeating the cycle from Step-02 to Step-04 until the start symbol is reached.
Advantages-
The advantages of operator precedence parsing are-
- The implementation is very easy and simple.
- The parser is quite powerful for expressions in programming languages.
Disadvantages-
The disadvantages of operator precedence parsing are-
- The handling of tokens known to have two different precedence becomes difficult.
- Only small class of grammars can be parsed using this parser.
Important Note-
- In practice, operator precedence table is not stored by the operator precedence parsers.
- This is because it occupies the large space.
- Instead, operator precedence parsers are implemented in a very unique style.
- They are implemented using operator precedence functions.
Operator Precedence Functions-
| Precedence functions perform the mapping of terminal symbols to the integers. |
- To decide the precedence relation between symbols, a numerical comparison is performed.
- It reduces the space complexity to a large extent.
Also Read- Shift Reduce Parsing
PRACTICE PROBLEMS BASED ON OPERATOR PRECEDENCE PARSING-
Problem-01:
Consider the following grammar-
E → EAE | id
A → + | x
Construct the operator precedence parser and parse the string id + id x id.
Solution-
Step-01:
We convert the given grammar into operator precedence grammar.
The equivalent operator precedence grammar is-
E → E + E | E x E | id
Step-02:
The terminal symbols in the grammar are { id, + , x , $ }
We construct the operator precedence table as-
| id | + | x | $ | |
| id | > | > | > | |
| + | < | > | < | > |
| x | < | > | > | > |
| $ | < | < | < |
Operator Precedence Table
Parsing Given String-
Given string to be parsed is id + id x id.
We follow the following steps to parse the given string-
Step-01:
We insert $ symbol at both ends of the string as-
$ id + id x id $
We insert precedence operators between the string symbols as-
$ < id > + < id > x < id > $
Step-02:
We scan and parse the string as-
$ < id > + < id > x < id > $
$ E + < id > x < id > $
$ E + E x < id > $
$ E + E x E $
$ + x $
$ < + < x > $
$ < + > $
$ $
Problem-02:
Consider the following grammar-
S → ( L ) | a
L → L , S | S
Construct the operator precedence parser and parse the string ( a , ( a , a ) ).
Solution-
The terminal symbols in the grammar are { ( , ) , a , , }
We construct the operator precedence table as-
| a | ( | ) | , | $ | |
| a | > | > | > | > | |
| ( | < | > | > | > | > |
| ) | < | > | > | > | > |
| , | < | < | > | > | > |
| $ | < | < | < | < |
Operator Precedence Table
Parsing Given String-
Given string to be parsed is ( a , ( a , a ) ).
We follow the following steps to parse the given string-
Step-01:
We insert $ symbol at both ends of the string as-
$ ( a , ( a , a ) ) $
We insert precedence operators between the string symbols as-
$ < ( < a > , < ( < a > , < a > ) > ) > $
Step-02:
We scan and parse the string as-
$ < ( < a > , < ( < a > , < a > ) > ) > $
$ < ( S , < ( < a > , < a > ) > ) > $
$ < ( S , < ( S , < a > ) > ) > $
$ < ( S , < ( S , S ) > ) > $
$ < ( S , < ( L , S ) > ) > $
$ < ( S , < ( L ) > ) > $
$ < ( S , S ) > $
$ < ( L , S ) > $
$ < ( L ) > $
$ < S > $
$ $
Problem-03:
Consider the following grammar-
E → E + E | E x E | id
- Construct Operator Precedence Parser.
- Find the Operator Precedence Functions.
Solution-
The terminal symbols in the grammar are { + , x , id , $ }
We construct the operator precedence table as-
| g → | |||||
| f ↓ | id | + | x | $ | |
| id | > | > | > | ||
| + | < | > | < | > | |
| x | < | > | > | > | |
| $ | < | < | < | ||
Operator Precedence Table
The graph representing the precedence functions is-
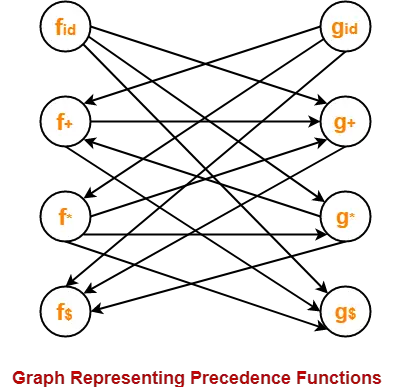
Here, the longest paths are-
- fid → gx → f+ → g+ → f$
- gid → fx → gx → f+ → g+ → f$
The resulting precedence functions are-
| + | x | id | $ | |
| f | 2 | 4 | 4 | 0 |
| g | 1 | 3 | 5 | 0 |
To gain better understanding about Operator Precedence Parsing,
Download Handwritten Notes Here-
Next Article- Three Address Code
Get more notes and other study material of Compiler Design.
Watch video lectures by visiting our YouTube channel LearnVidFun.
