Ambiguous Grammar & Parse Tree-
We have discussed-
- Ambiguous Grammar generates at least one string that has more than one parse tree.
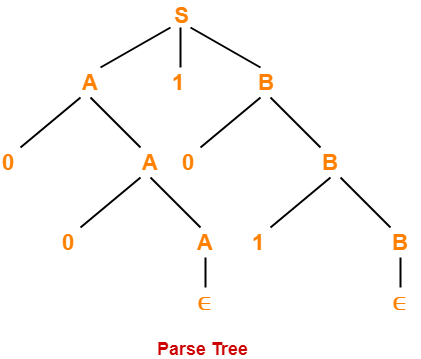
- Parse Tree is the geometrical representation of a derivation.
In this article, we will discuss important points about Ambiguous Grammar and Parse Tree.
Important Points-
Point-01:
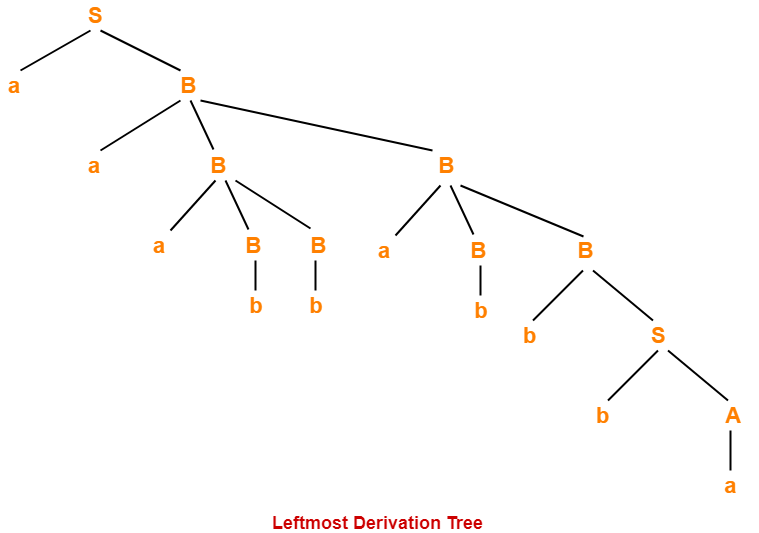
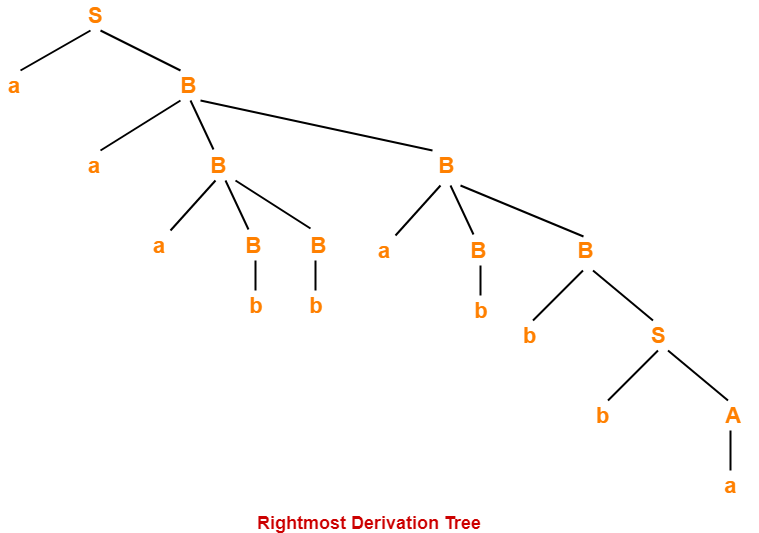
- There always exists a unique parse tree corresponding to each leftmost derivation and rightmost derivation.
|
If n parse trees exist for any string w, then there will be-
|
Point-02:
For ambiguous grammars,
- More than one leftmost derivation and more than one rightmost derivation exist for at least one string.
- Leftmost derivation and rightmost derivation represents different parse trees.
Point-03:
For unambiguous grammars,
- A unique leftmost derivation and a unique rightmost derivation exist for all the strings.
- Leftmost derivation and rightmost derivation represents the same parse tree.
Point-04:
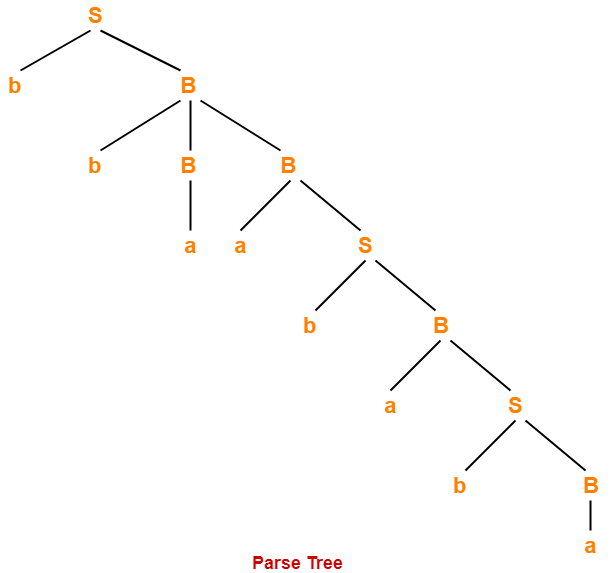
- There may exist derivations for a string which are neither leftmost nor rightmost.
Example
Consider the following grammar- S → ABC A → a B → b C → c
Consider a string w = abc. Total 6 derivations exist for string w. The following 4 derivations are neither leftmost nor rightmost-
Derivation-01:
S → ABC → aBC (Using A → a) → aBc (Using C → c) → abc (Using B → b)
Derivation-02:
S → ABC → AbC (Using B → b) → abC (Using A → a) → abc (Using C → c)
Derivation-03:
S → ABC → AbC (Using B → b) → Abc (Using C → c) → abc (Using A → a)
The other 2 derivations are leftmost derivation and rightmost derivation. |
Point-05:
- Leftmost derivation and rightmost derivation of a string may be exactly same.
- In fact, there may exist a grammar in which leftmost derivation and rightmost derivation is exactly same for all the strings.
Example
Consider the following grammar- S → aS / ∈
The language generated by this grammar is- L = { an , n>=0 } or a*
All the strings generated from this grammar have their leftmost derivation and rightmost derivation exactly same. Let us consider a string w = aaa.
Leftmost Derivation-
S → aS → aaS (Using S → aS) → aaaS (Using S → aS) → aaa∈ → aaa
Rightmost Derivation-
S → aS → aaS (Using S → aS) → aaaS (Using S → aS) → aaa∈ → aaa
Clearly, Leftmost derivation = Rightmost derivation Similar is the case for all other strings. |
Point-06:
- For a given parse tree, we may have its leftmost derivation exactly same as rightmost derivation.
Point-07:
- If for all the strings of a grammar, leftmost derivation is exactly same as rightmost derivation, then that grammar may be ambiguous or unambiguous.
Example
Consider the following grammar- S → aS / ∈
Now, consider the following grammar- S → aS / a / ∈
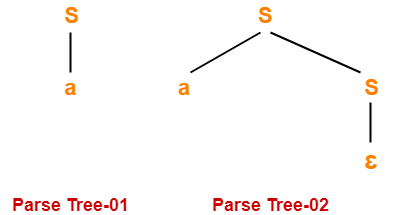
Consider a string w = a.
Since two different parse trees exist, so grammar is ambiguous.
Leftmost derivation and rightmost derivation for parse tree-01 are- S → a
Leftmost derivation and rightmost derivation for parse tree-02 are- S → aS S → a∈ S → a |
Next Article- Language of Grammar
Get more notes and other study material of Theory of Automata and Computation.
Watch video lectures by visiting our YouTube channel LearnVidFun.