Tag: shift reduce parsing example

Shift Reduce Parser | Shift Reduce Parsing

Compiler Design

Shift-Reduce Parser-

 

A shift-reduce parser is a bottom-up parser.

 

It takes the given input string and builds a parse tree-

  • Starting from the bottom at the leaves.
  • And growing the tree towards the top to the root.

 

 

Data Structures-

 

Two data structures are required to implement a shift-reduce parser-

  • A Stack is required to hold the grammar symbols.
  • An Input buffer is required to hold the string to be parsed.

 

Working-

 

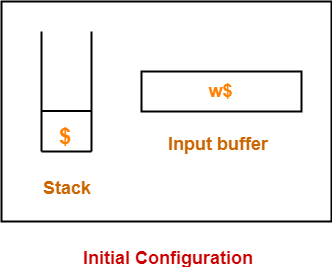
Initially, shift-reduce parser is present in the following configuration where-

  • Stack contains only the $ symbol.
  • Input buffer contains the input string with $ at its end.

 

 

The parser works by-

  • Moving the input symbols on the top of the stack.
  • Until a handle β appears on the top of the stack.

 

The parser keeps on repeating this cycle until-

  • An error is detected.
  • Or stack is left with only the start symbol and the input buffer becomes empty.

 

 

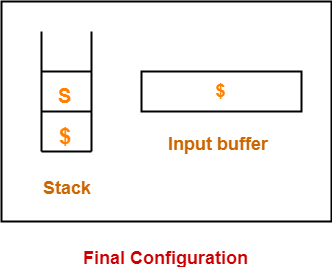
After achieving this configuration,

  • The parser stops / halts.
  • It reports the successful completion of parsing.

 

Possible Actions-

 

A shift-reduce parser can possibly make the following four actions-

 

1. Shift-

 

In a shift action,

  • The next symbol is shifted onto the top of the stack.

 

2. Reduce-

 

In a reduce action,

  • The handle appearing on the stack top is replaced with the appropriate non-terminal symbol.

 

3. Accept-

 

In an accept action,

  • The parser reports the successful completion of parsing.

 

4. Error-

 

In this state,

  • The parser becomes confused and is not able to make any decision.
  • It can neither perform shift action nor reduce action nor accept action.

 

Rules To Remember

 

It is important to remember the following rules while performing the shift-reduce action-

  • If the priority of incoming operator is more than the priority of in stack operator, then shift action is performed.
  • If the priority of in stack operator is same or less than the priority of in stack operator, then reduce action is performed.

 

PRACTICE PROBLEMS BASED ON SHIFT-REDUCE PARSING-

 

Problem-01:

 

Consider the following grammar-

E → E – E

E → E x E

E → id

Parse the input string id – id x id using a shift-reduce parser.

 

Solution-

 

The priority order is: id > x > –

 

Stack Input Buffer Parsing Action
$ id – id x id $ Shift
$ id – id x id $ Reduce E → id
$ E – id x id $ Shift
$ E – id x id $ Shift
$ E – id x id $ Reduce E → id
$ E – E x id $ Shift
$ E – E x id $ Shift
$ E – E x id $ Reduce E → id
$ E – E x E $ Reduce E → E x E
$ E – E $ Reduce E → E – E
$ E $ Accept

 

Problem-02:

 

Consider the following grammar-

S → ( L ) | a

L → L , S | S

Parse the input string ( a , ( a , a ) ) using a shift-reduce parser.

 

Solution-

 

Stack Input Buffer Parsing Action
$ ( a , ( a , a ) ) $ Shift
$ ( a , ( a , a ) ) $ Shift
$ ( a , ( a , a ) ) $ Reduce S → a
$ ( S , ( a , a ) ) $ Reduce L → S
$ ( L , ( a , a ) ) $ Shift
$ ( L , ( a , a ) ) $ Shift
$ ( L , ( a , a ) ) $ Shift
$ ( L , ( a , a ) ) $ Reduce S → a
$ ( L , ( S , a ) ) $ Reduce L → S
$ ( L , ( L , a ) ) $ Shift
$ ( L , ( L , a ) ) $ Shift
$ ( L , ( L , a ) ) $ Reduce S → a
$ ( L , ( L , S ) ) ) $ Reduce L → L , S
$ ( L , ( L ) ) $ Shift
$ ( L , ( L ) ) $ Reduce S → (L)
$ ( L , S ) $ Reduce L → L , S
$ ( L ) $ Shift
$ ( L ) $ Reduce S → (L)
$ S $ Accept

 

Problem-03:

 

Consider the following grammar-

S → T L

T → int | float

L → L , id | id

Parse the input string int id , id ; using a shift-reduce parser.

 

Solution-

 

Stack Input Buffer Parsing Action
$ int id , id ; $ Shift
$ int id , id ; $ Reduce T → int
$ T id , id ; $ Shift
$ T id , id ; $ Reduce L → id
$ T L , id ; $ Shift
$ T L , id ; $ Shift
$ T L , id ; $ Reduce L → L , id
$ T L ; $ Shift
$ T L ; $ Reduce S → T L
$ S $ Accept

 

Problem-04:

 

Considering the string “10201”, design a shift-reduce parser for the following grammar-

S → 0S0 | 1S1 | 2

 

Solution-

 

Stack Input Buffer Parsing Action
$ 1 0 2 0 1 $ Shift
$ 1 0 2 0 1 $ Shift
$ 1 0 2 0 1 $ Shift
$ 1 0 2 0 1 $ Reduce S → 2
$ 1 0 S 0 1 $ Shift
$ 1 0 S 0 1 $ Reduce S → 0 S 0
$ 1 S 1 $ Shift
$ 1 S 1 $ Reduce S → 1 S 1
$ S $ Accept

 

To gain better understanding about Shift-Reduce Parsing,

Watch this Video Lecture

 

Download Handwritten Notes Here-

 

 

Next Article- Operator Precedence Parsing

 

Get more notes and other study material of Compiler Design.

Watch video lectures by visiting our YouTube channel LearnVidFun.