Database Management System

Category: Database Management System

Candidate Key | Finding Candidate Keys | Examples

Keys in DBMS-

Before you go through this article, make sure that you have gone through the previous article on Keys in DBMS.

We have discussed-

A key is a set of attributes that can identify each tuple uniquely in the given relation.
There are various types of keys in DBMS-

In this article, we will discuss how to find candidate keys of a given relation.

Candidate Key-

A candidate key may be defined as-

A set of minimal attribute(s) that can identify each tuple uniquely in the given relation is called as a candidate key.

A minimal super key is called as a candidate key.

For any given relation,

It is possible to have multiple candidate keys.
There exists no general formula to find the total number of candidate keys of a given relation.

Example-

Consider the following Student schema-

Student ( roll , name , sex , age , address , class , section )

Given below are the examples of candidate keys-

( class , section , roll )
( name , address )

These are candidate keys because each set consists of minimal attributes required to identify each student uniquely in the Student table.

Finding Candidate Keys-

We can determine the candidate keys of a given relation using the following steps-

Step-01:

Determine all essential attributes of the given relation.
Essential attributes are those attributes which are not present on RHS of any functional dependency.
Essential attributes are always a part of every candidate key.
This is because they can not be determined by other attributes.

Example

Let R(A, B, C, D, E, F) be a relation scheme with the following functional dependencies-

A → B

C → D

D → E

Here, the attributes which are not present on RHS of any functional dependency are A, C and F.

So, essential attributes are- A, C and F.

Step-02:

The remaining attributes of the relation are non-essential attributes.
This is because they can be determined by using essential attributes.

Now, following two cases are possible-

Case-01:

If all essential attributes together can determine all remaining non-essential attributes, then-

The combination of essential attributes is the candidate key.
It is the only possible candidate key.

Case-02:

If all essential attributes together can not determine all remaining non-essential attributes, then-

The set of essential attributes and some non-essential attributes will be the candidate key(s).
In this case, multiple candidate keys are possible.
To find the candidate keys, we check different combinations of essential and non-essential attributes.

We will further understand how to find candidate keys with the help of following problems.

The following practice problems are based on Case-01.

PRACTICE PROBLEMS BASED ON FINDING CANDIDATE KEYS-

Problem-01:

Let R = (A, B, C, D, E, F) be a relation scheme with the following dependencies-

C → F

E → A

EC → D

A → B

Which of the following is a key for R?

Also, determine the total number of candidate keys and super keys.

Solution-

We will find candidate keys of the given relation in the following steps-

Step-01:

Determine all essential attributes of the given relation.
Essential attributes of the relation are- C and E.
So, attributes C and E will definitely be a part of every candidate key.

Step-02:

Now,

We will check if the essential attributes together can determine all remaining non-essential attributes.
To check, we find the closure of CE.

So, we have-

{ CE }⁺

= { C , E }

= { C , E , F } ( Using C → F )

= { A , C , E , F } ( Using E → A )

= { A , C , D , E , F } ( Using EC → D )

= { A , B , C , D , E , F } ( Using A → B )

We conclude that CE can determine all the attributes of the given relation.

So, CE is the only possible candidate key of the relation.

Thus, Option (B) is correct.

Total Number of Candidate Keys-

Only one candidate key CE is possible.

Total Number of Super Keys-

There are total 6 attributes in the given relation of which-

There are 2 essential attributes- C and E.
Remaining 4 attributes are non-essential attributes.
Essential attributes will be definitely present in every key.
Non-essential attributes may or may not be taken in every super key.

So, number of super keys possible = 2 x 2 x 2 x 2 = 16.

Thus, total number of super keys possible = 16.

Problem-02:

Let R = (A, B, C, D, E) be a relation scheme with the following dependencies-

AB → C

C → D

B → E

Determine the total number of candidate keys and super keys.

Solution-

We will find candidate keys of the given relation in the following steps-

Step-01:

Determine all essential attributes of the given relation.
Essential attributes of the relation are- A and B.
So, attributes A and B will definitely be a part of every candidate key.

Step-02:

Now,

We will check if the essential attributes together can determine all remaining non-essential attributes.
To check, we find the closure of AB.

So, we have-

{ AB }⁺

= { A , B }

= { A , B , C } ( Using AB → C )

= { A , B , C , D } ( Using C → D )

= { A , B , C , D , E } ( Using B → E )

We conclude that AB can determine all the attributes of the given relation.

Thus, AB is the only possible candidate key of the relation.

Total Number of Candidate Keys-

Only one candidate key AB is possible.

Total Number of Super Keys-

There are total 5 attributes in the given relation of which-

There are 2 essential attributes- A and B.
Remaining 3 attributes are non-essential attributes.
Essential attributes will be definitely present in every key.
Non-essential attributes may or may not be taken in every super key.

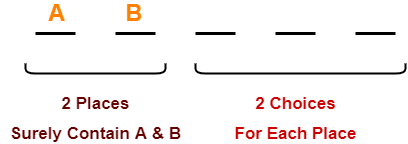
So, number of super keys possible = 2 x 2 x 2 = 8.

Thus, total number of super keys possible = 8.

Problem-03:

Consider the relation scheme R(E, F, G, H, I, J, K, L, M, N) and the set of functional dependencies-

{ E, F } → { G }

{ F } → { I , J }

{ E, H } → { K, L }

{ K } → { M }

{ L } → { N }

What is the key for R?

{ E, F }
{ E, F, H }
{ E, F, H, K, L }
{ E }

Also, determine the total number of candidate keys and super keys.

Solution-

We will find candidate keys of the given relation in the following steps-

Step-01:

Determine all essential attributes of the given relation.
Essential attributes of the relation are- E, F and H.
So, attributes E, F and H will definitely be a part of every candidate key.

Step-02:

Now,

We will check if the essential attributes together can determine all remaining non-essential attributes.
To check, we find the closure of EFH.

So, we have-

{ EFH }⁺

= { E , F , H }

= { E , F , G , H } ( Using EF → G )

= { E , F , G , H , I , J } ( Using F → IJ )

= { E , F , G , H , I , J , K , L } ( Using EH → KL )

= { E , F , G , H , I , J , K , L , M } ( Using K → M )

= { E , F , G , H , I , J , K , L , M , N } ( Using L → N )

We conclude that EFH can determine all the attributes of the given relation.

So, EFH is the only possible candidate key of the relation.

Thus, Option (B) is correct.

Total Number of Candidate Keys-

Only one candidate key EFH is possible.

Total Number of Super Keys-

There are total 10 attributes in the given relation of which-

There are 3 essential attributes- E, F and H.
Remaining 7 attributes are non-essential attributes.
Essential attributes will be definitely present in every key.
Non-essential attributes may or may not be taken in every super key.

So, number of super keys possible = 2 x 2 x 2 x 2 x 2 x 2 x 2 = 128.

Thus, total number of super keys possible = 128.

Problem-04:

Consider the relation scheme R(A, B, C, D, E, H) and the set of functional dependencies-

A → B

BC → D

E → C

D → A

What are the candidate keys of R?

AE, BE
AE, BE, DE
AEH, BEH, BCH
AEH, BEH, DEH

Solution-

We will find candidate keys of the given relation in the following steps-

Step-01:

Determine all essential attributes of the given relation.
Essential attributes of the relation are- E and H.
So, attributes E and H will definitely be a part of every candidate key.

The only possible option is (D).

Thus, Option (D) is correct.

Next Article- Functional Dependency in DBMS

Get more notes and other study material of Database Management System (DBMS).

Watch video lectures by visiting our YouTube channel LearnVidFun.

Set Theory Operators | Relational Algebra | DBMS

Database Management System

Relational Algebra Operators-

Before you go through this article, make sure that you have gone through the previous article on Introduction to Relational Algebra.

The operators in relational algebra are classified as-

In this article, we will discuss about Set Theory Operators.

Set Theory Operators-

Following operators are called as set theory operators-

Union Operator (∪)
Intersection Operator (∩)
Difference Operator (-)

Condition For Using Set Theory Operators

To use set theory operators on two relations,

The two relations must be union compatible.

Union compatible property means-

Both the relations must have same number of attributes.
The attribute domains (types of values accepted by attributes) of both the relations must be compatible.

Also read- Selection Operator and Projection Operator

1. Union Operator (∪)-

Let R and S be two relations.

Then-

R ∪ S is the set of all tuples belonging to either R or S or both.
In R ∪ S, duplicates are automatically removed.
Union operation is both commutative and associative.

Example-

Consider the following two relations R and S-

ID	Name	Subject
100	Ankit	English
200	Pooja	Maths
300	Komal	Science

Relation R

ID	Name	Subject
100	Ankit	English
400	Kajol	French

Relation S

Then, R ∪ S is-

ID	Name	Subject
100	Ankit	English
200	Pooja	Maths
300	Komal	Science
400	Kajol	French

Relation R ∪ S

2. Intersection Operator (∩)-

Let R and S be two relations.

Then-

R ∩ S is the set of all tuples belonging to both R and S.
In R ∩ S, duplicates are automatically removed.
Intersection operation is both commutative and associative.

Example-

Consider the following two relations R and S-

ID	Name	Subject
100	Ankit	English
200	Pooja	Maths
300	Komal	Science

Relation R

ID	Name	Subject
100	Ankit	English
400	Kajol	French

Relation S

Then, R ∩ S is-

ID	Name	Subject
100	Ankit	English

Relation R ∩ S

3. Difference Operator (-)-

Let R and S be two relations.

Then-

R – S is the set of all tuples belonging to R and not to S.
In R – S, duplicates are automatically removed.
Difference operation is associative but not commutative.

Example-

Consider the following two relations R and S-

ID	Name	Subject
100	Ankit	English
200	Pooja	Maths
300	Komal	Science

Relation R

ID	Name	Subject
100	Ankit	English
400	Kajol	French

Relation S

Then, R – S is-

ID	Name	Subject
200	Pooja	Maths
300	Komal	Science

Relation R – S

Get more notes and other study material of Database Management System (DBMS).

Watch video lectures by visiting our YouTube channel LearnVidFun.

Projection Operator | Relational Algebra | DBMS

Database Management System

Relational Algebra Operators-

Before you go through this article, make sure that you have gone through the previous article on Introduction to Relational Algebra.

The operators in relational algebra are classified as-

In this article, we will discuss about Projection Operator.

Projection Operator-

Projection Operator (π) is a unary operator in relational algebra that performs a projection operation.
It displays the columns of a relation or table based on the specified attributes.

Syntax-

π_{<attribute list>}(R)

Example-

Consider the following Student relation-

ID	Name	Subject	Age
100	Ashish	Maths	19
200	Rahul	Science	20
300	Naina	Physics	20
400	Sameer	Chemistry	21

Student

Then, we have-

Result for Query π_{Name, Age}(Student)-

Name	Age
Ashish	19
Rahul	20
Naina	20
Sameer	21

Result for Query π_{ID , Name}(Student)-

ID	Name
100	Ashish
200	Rahul
300	Naina
400	Sameer

Important Points-

Point-01:

The degree of output relation (number of columns present) is equal to the number of attributes mentioned in the attribute list.

Point-02:

Projection operator automatically removes all the duplicates while projecting the output relation.
So, cardinality of the original relation and output relation may or may not be same.
If there are no duplicates in the original relation, then the cardinality will remain same otherwise it will surely reduce.

Point-03:

If attribute list is a super key on relation R, then we will always get the same number of tuples in the output relation.
This is because then there will be no duplicates to filter.

Point-04:

Projection operator does not obey commutative property i.e.

π _<list2> (π _<list1>(R)) ≠ π _<list1> (π _<list2>(R))

Point-05:

Following expressions are equivalent because both finally projects columns of list-1

π _<list1> (π _<list2>(R)) = π _<list1>(R)

Point-06:

Selection Operator performs horizontal partitioning of the relation.
Projection operator performs vertical partitioning of the relation.

Point-07:

There is only one difference between projection operator of relational algebra and SELECT operation of SQL.
Projection operator does not allow duplicates while SELECT operation allows duplicates.
To avoid duplicates in SQL, we use “distinct” keyword and write SELECT distinct.
Thus, projection operator of relational algebra is equivalent to SELECT operation of SQL.

Next Article- Set Theory Operators in Relational Algebra

Get more notes and other study material of Database Management System (DBMS).

Watch video lectures by visiting our YouTube channel LearnVidFun.

Selection Operator | Relational Algebra | DBMS

Database Management System

Relational Algebra Operators-

Before you go through this article, make sure that you have gone through the previous article on Introduction to Relational Algebra.

The operators in relational algebra are classified as-

In this article, we will discuss about Selection Operator.

Selection Operator-

Selection Operator (σ) is a unary operator in relational algebra that performs a selection operation.
It selects those rows or tuples from the relation that satisfies the selection condition.

Syntax-

σ_{<selection_condition>}(R)

Examples-

Select tuples from a relation “Books” where subject is “database”

σ_{subject = “database”} (Books)

Select tuples from a relation “Books” where subject is “database” and price is “450”

σ_{subject = “database” ∧ price = “450”} (Books)

Select tuples from a relation “Books” where subject is “database” and price is “450” or have a publication year after 2010

σ_{subject = “database” ∧ price = “450” ∨ year >”2010″} (Books)

Important Points-

Point-01:

We may use logical operators like ∧ , ∨ , ! and relational operators like = , ≠ , > , < , <= , >= with the selection condition.

Point-02:

Selection operator only selects the required tuples according to the selection condition.
It does not display the selected tuples.
To display the selected tuples, projection operator is used.

Point-03:

Selection operator always selects the entire tuple. It can not select a section or part of a tuple.

Point-04:

Selection operator is commutative in nature i.e.

σ _{A ∧ B} (R) = σ _{B ∧ A} (R)

σ _B(σ _A(R)) = σ _A(σ _B(R))

Point-05:

Degree of the relation from a selection operation is same as degree of the input relation.

Point-06:

The number of rows returned by a selection operation is obviously less than or equal to the number of rows in the original table.

Thus,

Minimum Cardinality = 0
Maximum Cardinality = |R|

Next Article- Projection Operation in Relational Algebra

Get more notes and other study material of Database Management System (DBMS).

Watch video lectures by visiting our YouTube channel LearnVidFun.

Relational Algebra | Relational Algebra in DBMS

Database Management System

Relational Algebra-

Relational Algebra is a procedural query language which takes a relation as an input and generates a relation as an output.

Relational Algebra Operators-

The operators in relational algebra may be classified as-

We will discuss all these operators one by one in detail.

Characteristics-

Following are the important characteristics of relational operators-

Relational Operators always work on one or more relational tables.
Relational Operators always produce another relational table.
The table produced by a relational operator has all the properties of a relational model.

Next Article- Selection Operator in Relational Algebra

Get more notes and other study material of Database Management System (DBMS).

Watch video lectures by visiting our YouTube channel LearnVidFun.

← Older Posts

Category: Database Management System

Keys in DBMS-

Candidate Key-

Example-

Finding Candidate Keys-

Step-01:

Example

Step-02:

Case-01:

Case-02:

PRACTICE PROBLEMS BASED ON FINDING CANDIDATE KEYS-

Problem-01:

Solution-

Step-01:

Total Number of Candidate Keys-

Total Number of Super Keys-

Problem-02:

Solution-

Step-01:

Total Number of Candidate Keys-

Total Number of Super Keys-

Problem-03:

Solution-

Step-01:

Total Number of Candidate Keys-

Total Number of Super Keys-

Problem-04:

Solution-

Step-01:

Relational Algebra Operators-

Set Theory Operators-

Condition For Using Set Theory Operators

1. Union Operator (∪)-

Example-

Relation R

Relation S

Relation R ∪ S

2. Intersection Operator (∩)-

Example-

Relation R

Relation S

Relation R ∩ S

3. Difference Operator (-)-

Example-

Relation R

Relation S

Relation R – S

Relational Algebra Operators-

Projection Operator-

Syntax-

Example-

Student

Result for Query πName, Age(Student)-

Result for Query πID , Name(Student)-

Important Points-

Point-01:

Point-02:

Point-03:

Point-04:

Point-05:

Point-06:

Point-07:

Relational Algebra Operators-

Selection Operator-

Syntax-

Examples-

Important Points-

Point-01:

Point-02:

Point-03:

Point-04:

Point-05:

Point-06:

Relational Algebra-

Relational Algebra Operators-

Characteristics-

Result for Query π_{Name, Age}(Student)-

Result for Query π_{ID , Name}(Student)-