Category: Machine Learning

Linear Regression Machine Learning | Examples

Machine Learning

Linear Regression-

 

In Machine Learning,

  • Linear Regression is a supervised machine learning algorithm.
  • It tries to find out the best linear relationship that describes the data you have.
  • It assumes that there exists a linear relationship between a dependent variable and independent variable(s).
  • The value of the dependent variable of a linear regression model is a continuous value i.e. real numbers.

 

Also Read- Machine Learning Algorithms

 

Representing Linear Regression Model-

 

Linear regression model represents the linear relationship between a dependent variable and independent variable(s) via a sloped straight line.

 

 

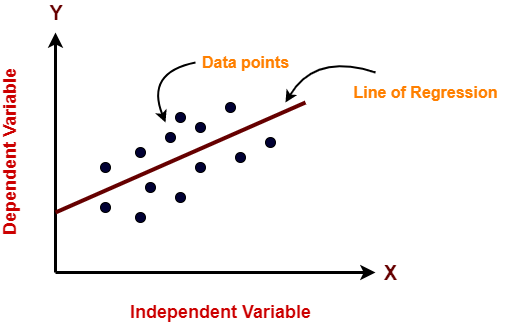
The sloped straight line representing the linear relationship that fits the given data best is called as a regression line.

It is also called as best fit line.

 

Types of Linear Regression-

 

Based on the number of independent variables, there are two types of linear regression-

 

 

  1. Simple Linear Regression
  2. Multiple Linear Regression

 

1. Simple Linear Regression-

 

In simple linear regression, the dependent variable depends only on a single independent variable.

 

For simple linear regression, the form of the model is-

Y = β0 + β1X

 

Here,

  • Y is a dependent variable.
  • X is an independent variable.
  • β0 and β1 are the regression coefficients.
  • β0 is the intercept or the bias that fixes the offset to a line.
  • β1 is the slope or weight that specifies the factor by which X has an impact on Y.

 

There are following 3 cases possible-

 

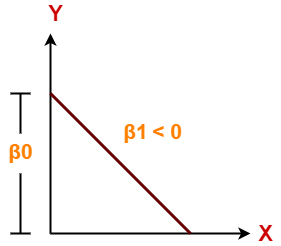
Case-01: β1 < 0

 

  • It indicates that variable X has negative impact on Y.
  • If X increases, Y will decrease and vice-versa.

 

 

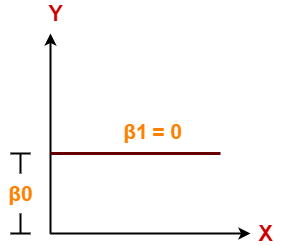
Case-02: β1 = 0

 

  • It indicates that variable X has no impact on Y.
  • If X changes, there will be no change in Y.

 

 

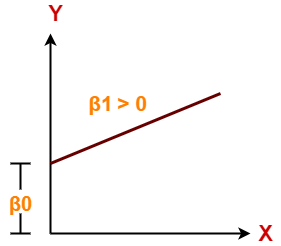
Case-03: β1 > 0

 

  • It indicates that variable X has positive impact on Y.
  • If X increases, Y will increase and vice-versa.

 

 

2. Multiple Linear Regression-

 

In multiple linear regression, the dependent variable depends on more than one independent variables.

 

For multiple linear regression, the form of the model is-

Y = β0 + β1X1 + β2X2 + β3X3 + …… + βnXn

 

Here,

  • Y is a dependent variable.
  • X1, X2, …., Xn are independent variables.
  • β0, β1,…, βn are the regression coefficients.
  • βj (1<=j<=n) is the slope or weight that specifies the factor by which Xj has an impact on Y.

 

To gain better understanding about Linear Regression,

Watch this Video Lecture

 

Get more notes and other study material of Machine Learning.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Machine Learning Workflow | Process Steps

Machine Learning

Machine Learning-

 

Before you go through this article, make sure that you have gone through the previous article on Machine Learning.

 

We have discussed-

  • Machine learning is building machines that can adapt and learn from experience.
  • Machine learning systems are not explicitly programmed.

 

In this article, we will discuss machine learning workflow.

 

Machine Learning Workflow-

 

Machine learning workflow refers to the series of stages or steps involved in the process of building a successful machine learning system.

 

The various stages involved in the machine learning workflow are-

 

 

  1. Data Collection
  2. Data Preparation
  3. Choosing Learning Algorithm
  4. Training Model
  5. Evaluating Model
  6. Predictions

 

Let us discuss each stage one by one.

 

1. Data Collection-

 

In this stage,

  • Data is collected from different sources.
  • The type of data collected depends upon the type of desired project.
  • Data may be collected from various sources such as files, databases etc.
  • The quality and quantity of gathered data directly affects the accuracy of the desired system.

 

2. Data Preparation-

 

In this stage,

  • Data preparation is done to clean the raw data.
  • Data collected from the real world is transformed to a clean dataset.
  • Raw data may contain missing values, inconsistent values, duplicate instances etc.
  • So, raw data cannot be directly used for building a model.

 

Different methods of cleaning the dataset are-

  • Ignoring the missing values
  • Removing instances having missing values from the dataset.
  • Estimating the missing values of instances using mean, median or mode.
  • Removing duplicate instances from the dataset.
  • Normalizing the data in the dataset.

 

This is the most time consuming stage in machine learning workflow.

 

3. Choosing Learning Algorithm-

 

In this stage,

  • The best performing learning algorithm is researched.
  • It depends upon the type of problem that needs to solved and the type of data we have.
  • If the problem is to classify and the data is labeled, classification algorithms are used.
  • If the problem is to perform a regression task and the data is labeled, regression algorithms are used.
  • If the problem is to create clusters and the data is unlabeled, clustering algorithms are used.

 

The following chart provides the overview of learning algorithms-

 

 

4. Training Model-

 

In this stage,

  • The model is trained to improve its ability.
  • The dataset is divided into training dataset and testing dataset.
  • The training and testing split is order of 80/20 or 70/30.
  • It also depends upon the size of the dataset.
  • Training dataset is used for training purpose.
  • Testing dataset is used for the testing purpose.
  • Training dataset is fed to the learning algorithm.
  • The learning algorithm finds a mapping between the input and the output and generates the model.

 

 

5. Evaluating Model-

 

In this stage,

  • The model is evaluated to test if the model is any good.
  • The model is evaluated using the kept-aside testing dataset.
  • It allows to test the model against data that has never been used before for training.
  • Metrics such as accuracy, precision, recall etc are used to test the performance.
  • If the model does not perform well, the model is re-built using different hyper parameters.
  • The accuracy may be further improved by tuning the hyper parameters.

 

 

6. Predictions-

 

In this stage,

  • The built system is finally used to do something useful in the real world.
  • Here, the true value of machine learning is realized.

 

To gain better understanding about Machine Learning Workflow,

Watch this Video Lecture

 

Next Article- Linear Regression

 

Get more notes and other study material of Machine Learning.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Machine Learning Algorithms | Machine Learning

Machine Learning

Machine Learning-

 

Learning is a continuous process of improvement over experience.

 

Machine learning is building machines that can adapt and learn from experience without being explicitly programmed.

 

In machine learning,

  • There is a learning algorithm.
  • Data called as training data set is fed to the learning algorithm.
  • Learning algorithm draws inferences from the training data set.
  • It generates a model which is a function that maps input to the output.

 

 

Machine Learning Applications-

 

Some important applications of machine learning are-

  • Spam Filtering
  • Fraudulent Transactions
  • Credit Scoring
  • Recommendations
  • Robot Navigation

 

Machine Learning Algorithms-

 

There are three types of machine learning algorithms-

 

 

  1. Supervised Learning
  2. Unsupervised Learning
  3. Reinforcement Learning

 

1. Supervised Learning-

 

In this type of machine learning algorithm,

  • The training data set is a labeled data set.
  • In other words, the training data set contains the input value (X) and target value (Y).
  • The learning algorithm generates a model.
  • Then, new data set consisting of only the input value is fed.
  • The model then generates the target value based on its learning.

 

 

Example-

 

Consider a sample database consisting of two columns where-

  • The first column specifies mails.
  • The second column specifies whether those emails are spam or not.

 

Mails (X) IsSpam (Y)
Mail-1 Yes
Mail-2 No
Mail-3 No
Mail-4 No

 

In this training data set, emails categorized as spam or not are done by a supervisor’s knowledge.

So, it is supervised learning algorithm.

 

Applications-

 

Some real-life applications are-

  • Spam Filtering
  • House Price Prediction
  • Credit Scoring (high risk or a low risk customer while lending loans by the banks)
  • Face Recognition etc

 

Types of Supervised Learning Algorithm-

 

There are two types of supervised learning algorithm-

 

 

  1. Regression
  2. Classification

 

Regression-

 

Here,

  • The target variable (Y) has continuous value.
  • Example- house price prediction

 

Classification-

 

Here,

  • The target variable (Y) has discrete values such as Yes or No, 0 or 1 and many more.
  • Example- Credit Scoring, Spam Filtering

 

2. Unsupervised Learning-

 

In this type of machine learning algorithm,

  • The training data set is an unlabeled data set.
  • In other words, the training data set contains only the input value (X) and not the target value (Y).
  • Based on the similarity between data, it tries to draw inference from the data such as finding patterns or clusters.

 

 

Applications-

 

Some real-life applications are-

  • Document Clustering
  • Finding fraudulent transactions

 

3. Reinforcement Learning-

 

In this type of machine learning algorithm,

  • The agent acts in an environment in order to maximize the rewards and minimize the penalty.
  • Unlike supervised learning, no data is provided to the agent.
  • The agent itself takes action or sequence of actions whether right or wrong to perform a task and learn from the experience.

 

Applications-

 

Some real-life applications are-

  • Game Playing
  • Robot Navigation

 

To gain better understanding about Machine Learning & its Algorithms,

Watch this Video Lecture

 

Next Article- Machine Learning Workflow

 

Get more notes and other study material of Machine Learning.

Watch video lectures by visiting our YouTube channel LearnVidFun.