Linear Regression-
In Machine Learning,
- Linear Regression is a supervised machine learning algorithm.
- It tries to find out the best linear relationship that describes the data you have.
- It assumes that there exists a linear relationship between a dependent variable and independent variable(s).
- The value of the dependent variable of a linear regression model is a continuous value i.e. real numbers.
Also Read- Machine Learning Algorithms
Representing Linear Regression Model-
Linear regression model represents the linear relationship between a dependent variable and independent variable(s) via a sloped straight line.
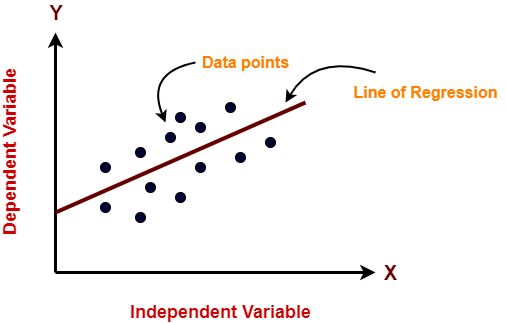
The sloped straight line representing the linear relationship that fits the given data best is called as a regression line.
It is also called as best fit line.
Types of Linear Regression-
Based on the number of independent variables, there are two types of linear regression-
- Simple Linear Regression
- Multiple Linear Regression
1. Simple Linear Regression-
In simple linear regression, the dependent variable depends only on a single independent variable.
For simple linear regression, the form of the model is-
Y = β0 + β1X
Here,
- Y is a dependent variable.
- X is an independent variable.
- β0 and β1 are the regression coefficients.
- β0 is the intercept or the bias that fixes the offset to a line.
- β1 is the slope or weight that specifies the factor by which X has an impact on Y.
There are following 3 cases possible-
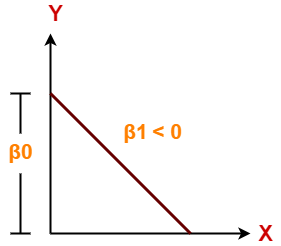
Case-01: β1 < 0
- It indicates that variable X has negative impact on Y.
- If X increases, Y will decrease and vice-versa.
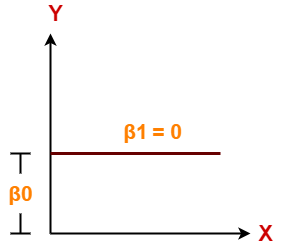
Case-02: β1 = 0
- It indicates that variable X has no impact on Y.
- If X changes, there will be no change in Y.
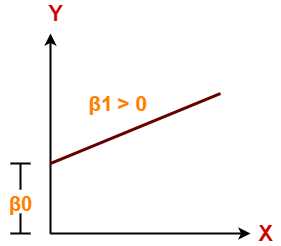
Case-03: β1 > 0
- It indicates that variable X has positive impact on Y.
- If X increases, Y will increase and vice-versa.
2. Multiple Linear Regression-
In multiple linear regression, the dependent variable depends on more than one independent variables.
For multiple linear regression, the form of the model is-
Y = β0 + β1X1 + β2X2 + β3X3 + …… + βnXn
Here,
- Y is a dependent variable.
- X1, X2, …., Xn are independent variables.
- β0, β1,…, βn are the regression coefficients.
- βj (1<=j<=n) is the slope or weight that specifies the factor by which Xj has an impact on Y.
To gain better understanding about Linear Regression,
Get more notes and other study material of Machine Learning.
Watch video lectures by visiting our YouTube channel LearnVidFun.

