cache memory | Gate Vidyalay

Tag: cache memory

Memory Organization in Computer Architecture

Computer Organization and Architecture

Memory Organization in Computer Architecture-

Before you go through this article, make sure that you have gone through the previous article on Memory Hierarchy.

In a computer,

Memory is organized at different levels.
CPU may try to access different levels of memory in different ways.
On this basis, the memory organization is broadly divided into two types-

Simultaneous Access Memory Organization
Hierarchical Access Memory Organization

1. Simultaneous Access Memory Organization-

In this memory organization,

All the levels of memory are directly connected to the CPU.
Whenever CPU requires any word, it starts searching for it in all the levels simultaneously.

Example-01:

Consider the following simultaneous access memory organization-

Here, two levels of memory are directly connected to the CPU.

Let-

T1 = Access time of level L1
S1 = Size of level L1
C1 = Cost per byte of level L1
H1 = Hit rate of level L1

Similar are the notations for level L2.

Average Memory Access Time-

Average time required to access memory per operation

= H1 x T1 + (1 – H1) x H2 x T2

= H1 x T1 + (1 – H1) x 1 x T2

= H1 x T1 + (1 – H1) x T2

Important Note

In any memory organization,

The data item being searched will definitely be present in the last level.
Thus, hit rate for the last level is always 1.

Average Cost Per Byte-

Average cost per byte of the memory

= { C1 x S1 + C2 x S2 } / { S1 + S2 }

Example-02:

Consider the following simultaneous access memory organization-

Here, three levels of memory are directly connected to the CPU.

Let-

T1 = Access time of level L1
S1 = Size of level L1
C1 = Cost per byte of level L1
H1 = Hit rate of level L1

Similar are the notations for other two levels.

Average Memory Access Time-

Average time required to access memory per operation

= H1 x T1 + (1 – H1) x H2 x T2 + (1 – H1) x (1 – H2) x H3 x T3

= H1 x T1 + (1 – H1) x H2 x T2 + (1 – H1) x (1 – H2) x 1 x T3

= H1 x T1 + (1 – H1) x H2 x T2 + (1 – H1) x (1 – H2) x T3

Average Cost Per Byte-

Average cost per byte of the memory

= { C1 x S1 + C2 x S2 + C3 x S3 } / { S1 + S2 + S3 }

2. Hierarchical Access Memory Organization-

In this memory organization, memory levels are organized as-

Level-1 is directly connected to the CPU.
Level-2 is directly connected to level-1.
Level-3 is directly connected to level-2 and so on.

Whenever CPU requires any word,

It first searches for the word in level-1.
If the required word is not found in level-1, it searches for the word in level-2.
If the required word is not found in level-2, it searches for the word in level-3 and so on.

Example-01:

Consider the following hierarchical access memory organization-

Here, two levels of memory are connected to the CPU in a hierarchical fashion.

Let-

T1 = Access time of level L1
S1 = Size of level L1
C1 = Cost per byte of level L1
H1 = Hit rate of level L1

Similar are the notations for level L2.

Average Memory Access Time-

Average time required to access memory per operation

= H1 x T1 + (1 – H1) x H2 x (T1 + T2)

= H1 x T1 + (1 – H1) x 1 x (T1 + T2)

= H1 x T1 + (1 – H1) x (T1 + T2)

Average Cost Per Byte-

Average cost per byte of the memory

= { C1 x S1 + C2 x S2 } / { S1 + S2 }

Example-02:

Consider the following hierarchical access memory organization-

Here, three levels of memory are connected to the CPU in a hierarchical fashion.

Let-

T1 = Access time of level L1
S1 = Size of level L1
C1 = Cost per byte of level L1
H1 = Hit rate of level L1

Similar are the notations for other two levels.

Average Memory Access Time-

Average time required to access memory per operation

= H1 x T1 + (1 – H1) x H2 x (T1 + T2) + (1 – H1) x (1 – H2) x H3 x (T1 + T2 + T3)

= H1 x T1 + (1 – H1) x H2 x (T1 + T2) + (1 – H1) x (1 – H2) x 1 x (T1 + T2 + T3)

= H1 x T1 + (1 – H1) x H2 x (T1 + T2) + (1 – H1) x (1 – H2) x (T1 + T2 + T3)

Average Cost Per Byte-

Average cost per byte of the memory

= { C1 x S1 + C2 x S2 + C3 x S3 } / { S1 + S2 + S3 }

PRACTICE PROBLEMS BASED ON MEMORY ORGANIZATION-

Problem-01:

What is the average memory access time for a machine with a cache hit rate of 80% and cache access time of 5 ns and main memory access time of 100 ns when-

Simultaneous access memory organization is used.
Hierarchical access memory organization is used.

Solution-

Part-01: Simultaneous Access Memory Organization-

The memory organization will be as shown-

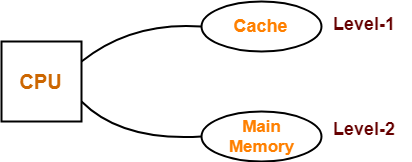
Average memory access time

= H1 x T1 + (1 – H1) x H2 x T2

= 0.8 x 5 ns + (1 – 0.8) x 1 x 100 ns

= 4 ns + 0.2 x 100 ns

= 4 ns + 20 ns

= 24 ns

Part-02: Hierarchical Access Memory Organization-

The memory organization will be as shown-

Average memory access time

= H1 x T1 + (1 – H1) x H2 x (T1 + T2)

= 0.8 x 5 ns + (1 – 0.8) x 1 x (5 ns + 100 ns)

= 4 ns + 0.2 x 105 ns

= 4 ns + 21 ns

= 25 ns

Problem-02:

A computer has a cache, main memory and a disk used for virtual memory. An access to the cache takes 10 ns. An access to main memory takes 100 ns. An access to the disk takes 10,000 ns. Suppose the cache hit ratio is 0.9 and the main memory hit ratio is 0.8. The effective access time required to access a referenced word on the system is _______ when-

Simultaneous access memory organization is used.
Hierarchical access memory organization is used.

Solution-

Part-01:Simultaneous Access Memory Organization-

The memory organization will be as shown-

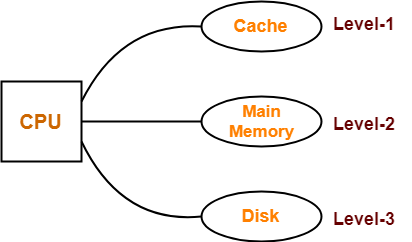
Effective memory access time

= H1 x T1 + (1 – H1) x H2 x T2 + (1 – H1) x (1 – H2) x H3 x T3

= 0.9 x 10 ns + (1 – 0.9) x 0.8 x 100 ns + (1 – 0.9) x (1 – 0.8) x 1 x 10000 ns

= 9 ns + 8 ns + 200 ns

= 217 ns

Part-02: Hierarchical Access Memory Organization-

The memory organization will be as shown-

Effective memory access time

= H1 x T1 + (1 – H1) x H2 x (T1 + T2) + (1 – H1) x (1 – H2) x H3 x (T1 + T2 + T3)

= 0.9 x 10 ns + (1 – 0.9) x 0.8 x (10 ns + 100 ns) + (1 – 0.9) x (1 – 0.8) x 1 x (10 ns + 100 ns + 10000 ns)

= 9 ns + 8.8 ns + 202.2 ns

= 220 ns

Important Note

While solving numerical problems

If the kind of memory organization used is not mentioned, assume hierarchical access memory organization.

To gain better understanding about Memory Organization,

Watch this Video Lecture

Next Article- Cache Memory

Get more notes and other study material of Computer Organization and Architecture.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Cache Line | Cache Line Size | Cache Memory

Computer Organization and Architecture

Cache Memory-

Before you go through this article, make sure that you have gone through the previous article on Cache Memory.

We have discussed-

Cache memory is a random access memory.
It lies on the path between the processor and the main memory.
It bridges the speed mismatch between the fastest processor and the slower main memory.

Also Read- Cache Mapping Techniques

Cache Lines-

Cache memory is divided into equal size partitions called as cache lines.

While designing a computer’s cache system, the size of cache lines is an important parameter.
The size of cache line affects a lot of parameters in the caching system.

The following results discuss the effect of changing the cache block (or line) size in a caching system.

Result-01: Effect of Changing Block Size on Spatial Locality-

The larger the block size, better will be the spatial locality.

Explanation-

Keeping the cache size constant, we have-

Case-01: Decreasing the Block Size-

A smaller block size will contain a smaller number of near by addresses in it.
Thus, only smaller number of near by addresses will be brought into the cache.
This increases the chances of cache miss which reduces the exploitation of spatial locality.
Thus, smaller is the block size, inferior is the spatial locality.

Case-02: Increasing the Block Size-

A larger block size will contain a larger number of near by addresses in it.
Thus, larger number of near by addresses will be brought into the cache.
This increases the chances of cache hit which increases the exploitation of spatial locality.
Thus, larger is the block size, better is the spatial locality.

Result-02: Effect of Changing Block Size On Cache Tag in Direct Mapped Cache-

In direct mapped cache, block size does not affect the cache tag anyhow.

Explanation-

Keeping the cache size constant, we have-

Case-01: Decreasing the Block Size-

Decreasing the block size increases the number of lines in cache.
With the decrease in block size, the number of bits in block offset decreases.
However, with the increase in the number of cache lines, number of bits in line number increases.
So, number of bits in line number + number of bits in block offset = remains constant.
Thus, there is no effect on the cache tag.

Example-

Case-02: Increasing the Block Size-

Increasing the block size decreases the number of lines in cache.
With the increase in block size, the number of bits in block offset increases.
However, with the decrease in the number of cache lines, number of bits in line number decreases.
Thus, number of bits in line number + number of bits in block offset = remains constant.
Thus, there is no effect on the cache tag.

Example-

Result-03: Effect of Changing Block Size On Cache Tag in Fully Associative Cache-

In fully associative cache, on decreasing block size, cache tag is reduced and vice versa.

Explanation-

Keeping the cache size constant, we have-

Case-01: Decreasing the Block Size-

Decreasing the block size decreases the number of bits in block offset.
With the decrease in number of bits in block offset, number of bits in tag increases.

Case-02: Increasing the Block Size-

Increasing the block size increases the number of bits in block offset.
With the increase in number of bits in block offset, number of bits in tag decreases.

Result-04: Effect of Changing Block Size On Cache Tag in Set Associative Cache-

In set associative cache, block size does not affect cache tag anyhow.

Explanation-

Keeping the cache size constant, we have-

Case-01: Decreasing the Block Size-

Decreasing the block size increases the number of lines in cache.
With the decrease in block size, number of bits in block offset decreases.
With the increase in the number of cache lines, number of sets in cache increases.
With the increase in number of sets in cache, number of bits in set number increases.
So, number of bits in set number + number of bits in block offset = remains constant.
Thus, there is no effect on the cache tag.

Example-

Case-02: Increasing the Block Size-

Increasing the block size decreases the number of lines in cache.
With the increase in block size, number of bits in block offset increases.
With the decrease in the number of cache lines, number of sets in cache decreases.
With the decrease in number of sets in cache, number of bits in set number decreases.
So, number of bits in set number + number of bits in block offset = remains constant.
Thus, there is no effect on the cache tag.

Example-

Result-05: Effect of Changing Block Size On Cache Miss Penalty-

A smaller cache block incurs a lower cache miss penalty.

Explanation-

When a cache miss occurs, block containing the required word has to be brought from the main memory.
If the block size is small, then time taken to bring the block in the cache will be less.
Hence, less miss penalty will incur.
But if the block size is large, then time taken to bring the block in the cache will be more.
Hence, more miss penalty will incur.

Result-06: Effect of Cache Tag On Cache Hit Time-

A smaller cache tag ensures a lower cache hit time.

Explanation-

Cache hit time is the time required to find out whether the required block is in cache or not.
It involves comparing the tag of generated address with the tag of cache lines.
Smaller is the cache tag, lesser will be the time taken to perform the comparisons.
Hence, smaller cache tag ensures lower cache hit time.
On the other hand, larger is the cache tag, more will be time taken to perform the comparisons.
Thus, larger cache tag results in higher cache hit time.

PRACTICE PROBLEM BASED ON CACHE LINE-

Problem-

In designing a computer’s cache system, the cache block or cache line size is an important parameter. Which of the following statements is correct in this context?

A smaller block size implies better spatial locality
A smaller block size implies a smaller cache tag and hence lower cache tag overhead
A smaller block size implies a larger cache tag and hence lower cache hit time
A smaller bock size incurs a lower cache miss penalty

Solution-

Option (D) is correct. (Result-05)

Reasons-

Option (A) is incorrect because-

Smaller block does not imply better spatial locality.
Always, Larger the block size, better is the spatial locality.

Option (B) is incorrect because-

In direct mapped cache and set associative cache, there is no effect of changing block size on cache tag.
In fully associative mapped cache, on decreasing block size, cache tag becomes larger.
Thus, smaller block size does not imply smaller cache tag in any cache organization.

Option (C) is incorrect because-

“A smaller block size implies a larger cache tag” is true only for fully associative mapped cache.
Larger cache tag does not imply lower cache hit time rather cache hit time is increased.

Next Article- Magnetic Disk | Important Formulas

Get more notes and other study material of Computer Organization and Architecture.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Fully Associative Mapping | Practice Problems

Computer Organization and Architecture

Fully Associative Mapping-

Before you go through this article, make sure that you have gone through the previous article on Cache Mapping.

In fully associative mapping,

A block of main memory can be mapped to any freely available cache line.
This makes fully associative mapping more flexible than direct mapping.
A replacement algorithm is needed to replace a block if the cache is full.

In this article, we will discuss practice problems based on fully associative mapping.

Also Read- Practice Problems On Direct Mapping

PRACTICE PROBLEMS BASED ON FULLY ASSOCIATIVE MAPPING-

Problem-01:

Consider a fully associative mapped cache of size 16 KB with block size 256 bytes. The size of main memory is 128 KB. Find-

Number of bits in tag
Tag directory size

Solution-

Given-

Cache memory size = 16 KB
Block size = Frame size = Line size = 256 bytes
Main memory size = 128 KB

We consider that the memory is byte addressable.

Number of Bits in Physical Address-

We have,

Size of main memory

= 128 KB

= 2¹⁷ bytes

Thus, Number of bits in physical address = 17 bits

Number of Bits in Block Offset-

We have,

Block size

= 256 bytes

= 2⁸ bytes

Thus, Number of bits in block offset = 8 bits

Number of Bits in Tag-

Number of bits in tag

= Number of bits in physical address – Number of bits in block offset

= 17 bits – 8 bits

= 9 bits

Thus, Number of bits in tag = 9 bits

Number of Lines in Cache-

Total number of lines in cache

= Cache size / Line size

= 16 KB / 256 bytes

= 2¹⁴ bytes / 2⁸ bytes

= 2⁶ lines

Tag Directory Size-

Tag directory size

= Number of tags x Tag size

= Number of lines in cache x Number of bits in tag

= 2⁶ x 9 bits

= 576 bits

= 72 bytes

Thus, size of tag directory = 72 bytes

Problem-02:

Consider a fully associative mapped cache of size 512 KB with block size 1 KB. There are 17 bits in the tag. Find-

Size of main memory
Tag directory size

Solution-

Given-

Cache memory size = 512 KB
Block size = Frame size = Line size = 1 KB
Number of bits in tag = 17 bits

We consider that the memory is byte addressable.

Number of Bits in Block Offset-

We have,

Block size

= 1 KB

= 2¹⁰ bytes

Thus, Number of bits in block offset = 10 bits

Number of Bits in Physical Address-

Number of bits in physical address

= Number of bits in tag + Number of bits in block offset

= 17 bits + 10 bits

= 27 bits

Thus, Number of bits in physical address = 27 bits

Size of Main Memory-

We have,

Number of bits in physical address = 27 bits

Thus, Size of main memory

= 2²⁷ bytes

= 128 MB

Number of Lines in Cache-

Total number of lines in cache

= Cache size / Line size

= 512 KB / 1 KB

= 512 lines

= 2⁹ lines

Tag Directory Size-

Tag directory size

= Number of tags x Tag size

= Number of lines in cache x Number of bits in tag

= 2⁹ x 17 bits

= 8704 bits

= 1088 bytes

Thus, size of tag directory = 1088 bytes

Also Read- Practice Problems On Set Associative Mapping

Problem-03:

Consider a fully associative mapped cache with block size 4 KB. The size of main memory is 16 GB. Find the number of bits in tag.

Solution-

Given-

Block size = Frame size = Line size = 4 KB
Size of main memory = 16 GB

We consider that the memory is byte addressable.

Number of Bits in Physical Address-

We have,

Size of main memory

= 16 GB

= 2³⁴ bytes

Thus, Number of bits in physical address = 34 bits

Number of Bits in Block Offset-

We have,

Block size

= 4 KB

= 2¹² bytes

Thus, Number of bits in block offset = 12 bits

Number of Bits in Tag-

Number of bits in tag

= Number of bits in physical address – Number of bits in block offset

= 34 bits – 12 bits

= 22 bits

Thus, Number of bits in tag = 22 bits

To watch video solutions and practice more problems,

Watch this Video Lecture

Next Article- Set Associative Mapping | Implementation & Formulas

Get more notes and other study material of Computer Organization and Architecture.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Cache Memory in Computer Architecture

Computer Organization and Architecture

Cache Memory-

Cache memory is a Random Access Memory.
The main advantage of cache memory is its very fast speed.
It can be accessed by the CPU at much faster speed than main memory.

Location-

Cache memory lies on the path between the CPU and the main memory.
It facilitates the transfer of data between the processor and the main memory at the speed which matches to the speed of the processor.

Data is transferred in the form of words between the cache memory and the CPU.
Data is transferred in the form of blocks or pages between the cache memory and the main memory.

Purpose-

The fast speed of the cache memory makes it extremely useful.
It is used for bridging the speed mismatch between the fastest CPU and the main memory.
It does not let the CPU performance suffer due to the slower speed of the main memory.

Execution Of Program-

Whenever any program has to be executed, it is first loaded in the main memory.
The portion of the program that is mostly probably going to be executed in the near future is kept in the cache memory.
This allows CPU to access the most probable portion at a faster speed.

Step-01:

Whenever CPU requires any word of memory, it is first searched in the CPU registers.

Now, there are two cases possible-

Case-01:

If the required word is found in the CPU registers, it is read from there.

Case-02:

If the required word is not found in the CPU registers, Step-02 is followed.

Step-02:

When the required word is not found in the CPU registers, it is searched in the cache memory.
Tag directory of the cache memory is used to search whether the required word is present in the cache memory or not.

Now, there are two cases possible-

Case-01:

If the required word is found in the cache memory, the word is delivered to the CPU.
This is known as Cache hit.

Case-02:

If the required word is not found in the cache memory, Step-03 is followed.
This is known as Cache miss.

Step-03:

When the required word is not found in the cache memory, it is searched in the main memory.
Page Table is used to determine whether the required page is present in the main memory or not.

Now, there are two cases possible-

Case-01:

If the page containing the required word is found in the main memory,

The page is mapped from the main memory to the cache memory.
This mapping is performed using cache mapping techniques.
Then, the required word is delivered to the CPU.

Case-02:

If the page containing the required word is not found in the main memory,

A page fault occurs.
The page containing the required word is mapped from the secondary memory to the main memory.
Then, the page is mapped from the main memory to the cache memory.
Then, the required word is delivered to the CPU.

Multilevel Cache Organization-

A multilevel cache organization is an organization where cache memories of different sizes are organized at multiple levels to increase the processing speed to a greater extent.
The smaller the size of cache, the faster its speed.
The smallest size cache memory is placed closest to the CPU.
This helps to achieve better performance in terms of speed.

Example-

Three level cache organization consists of three cache memories of different size organized at three different levels as shown below-

Size (L1 Cache) < Size (L2 Cache) < Size (L3 Cache) < Size (Main Memory)

To gain better understanding about Cache Memory,

Watch this Video Lecture

Next Article- Cache Mapping Techniques

Get more notes and other study material of Computer Organization and Architecture.

Watch video lectures by visiting our YouTube channel LearnVidFun.