Number System Conversions-
Before you go through this article, make sure that you have gone through the previous article on Basics of Number System.
In number system,
- It is very important to have a good knowledge of how to convert numbers from one base to another base.
- Here, we will learn how to convert any given number from base 10 to base 8.

Decimal to Octal Conversion-
A given number can be converted from base 10 to any other base using division method and multiplication method.
Following two cases are possible-
Case-01: For Numbers Carrying No Fractional Part-
- Division Method is used to convert such numbers from base 10 to another base.
- The division is performed with the required base.
Steps To Convert From Base 10 to Base 8-
- Divide the given number (in base 10) with 8 until the result finally left is less than 8.
- Traverse the remainders from bottom to top to get the required number in base 8.
Case-02: For Numbers Carrying A Fractional Part-
To convert such numbers from base 10 to another base, real part and fractional part are treated separately.
For Real Part-
The steps involved in converting the real part from base 10 to another base are same as above.
For Fractional Part-
- Multiplication Method is used to convert fractional part from base 10 to another base.
- The multiplication is performed with the required base.
Steps To Convert From Base 10 To Base 8-
- Multiply the given fraction (in base 10) with 8.
- Write the real part and fractional part of the result so obtained separately.
- Multiply the fractional part with 8.
- Write the real part and fractional part of the result so obtained separately.
- Repeat this procedure until the fractional part remains 0.
- If fractional part does not terminate to 0, find the result up to as many places as required.
Required Number in Base 8
= Series of real part of multiplication results obtained in the above steps from top to bottom
Also Read- Conversion to Base 10
PRACTICE PROBLEMS BASED ON DECIMAL TO OCTAL CONVERSION-
Problems-
Convert the following numbers from base 10 to base 8-
- (1032)10
- (1032.6875)10
- (172)10
- (172.878)10
Solution-
1. (1032)10
(1032)10 → (?)8
Using division method, we have-
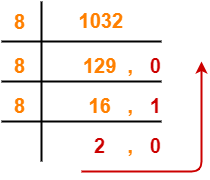
From here, (1032)10 = (2010)8
2. (1032.6875)10
(1032.6875)10 → ( ? )8
Here, we treat the real part and fractional part separately-
For Real Part-
- The real part is (1032)10
- We convert the real part from base 10 to base 8 using division method same as above.
So, (1032)10 = (2010)8
For Fractional Part-
- The fractional part is (0.6875)10
- We convert the fractional part from base 10 to base 8 using multiplication method.
Using multiplication method, we have-
| Real part | Fractional Part | |
| 0.6875 x 8 | 5 | 0.5 |
| 0.5 x 8 | 4 | 0.0 |
Explanation
Step-01:
Step-02:
Since fractional part becomes 0, so we stop. |
- The fractional part terminates to 0 after 2 iterations.
- Traverse the real part column from top to bottom to obtain the required number in base 8.
From here, (0.6875)10 = (0.54)8
Combining the result of real and fractional parts, we have-
(1032.6875)10 = (2010.54)8
3. (172)10
(172)10 → ( ? )8
Using division method, we have-
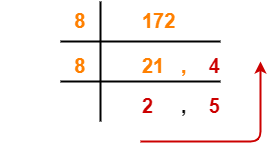
From here, (172)10 = (254)8
4. (172.878)10
(172.878)10 → ( ? )8
Here, we treat the real part and fractional part separately-
For Real Part-
- The real part is (172)10
- We convert the real part from base 10 to base 8 using division method same as above.
So, (172)10 = (254)8
For Fractional Part-
- The fractional part is (0.878)10
- We convert the fractional part from base 10 to base 8 using multiplication method.
Using multiplication method, we have-
| Real part | Fractional Part | |
| 0.878 x 8 | 7 | 0.024 |
| 0.024 x 8 | 0 | 0.192 |
| 0.192 x 8 | 1 | 0.536 |
| 0.536 x 8 | 4 | 0.288 |
- The fractional part does not terminates to 0 after several iterations.
- So, let us find the value up to 4 decimal places.
- Traverse the real part column from top to bottom to obtain the required number in base 8.
From here, (0.878)10 = (0.7014)8
Combining the result of real and fractional parts, we have-
(172.878)10 = (254.7014)8
Also Read- Decimal to Binary Conversion
To gain better understanding about Decimal to Octal Conversion,
Next Article- Decimal to Hexadecimal Conversion
Get more notes and other study material of Number System.
Watch video lectures by visiting our YouTube channel LearnVidFun.