Floyd Warshall Algorithm-
- Floyd Warshall Algorithm is a famous algorithm.
- It is used to solve All Pairs Shortest Path Problem.
- It computes the shortest path between every pair of vertices of the given graph.
- Floyd Warshall Algorithm is an example of dynamic programming approach.
Also Read- Shortest Path Problem
Advantages-
Floyd Warshall Algorithm has the following main advantages-
- It is extremely simple.
- It is easy to implement.
Algorithm-
Floyd Warshall Algorithm is as shown below-
Create a |V| x |V| matrix // It represents the distance between every pair of vertices as given
For each cell (i,j) in M do-
if i = = j
M[ i ][ j ] = 0 // For all diagonal elements, value = 0
if (i , j) is an edge in E
M[ i ][ j ] = weight(i,j) // If there exists a direct edge between the vertices, value = weight of edge
else
M[ i ][ j ] = infinity // If there is no direct edge between the vertices, value = ∞
for k from 1 to |V|
for i from 1 to |V|
for j from 1 to |V|
if M[ i ][ j ] > M[ i ][ k ] + M[ k ][ j ]
M[ i ][ j ] = M[ i ][ k ] + M[ k ][ j ]
Time Complexity-
- Floyd Warshall Algorithm consists of three loops over all the nodes.
- The inner most loop consists of only constant complexity operations.
- Hence, the asymptotic complexity of Floyd Warshall algorithm is O(n3).
- Here, n is the number of nodes in the given graph.
When Floyd Warshall Algorithm Is Used?
- Floyd Warshall Algorithm is best suited for dense graphs.
- This is because its complexity depends only on the number of vertices in the given graph.
- For sparse graphs, Johnson’s Algorithm is more suitable.
PRACTICE PROBLEM BASED ON FLOYD WARSHALL ALGORITHM-
Problem-
Consider the following directed weighted graph-
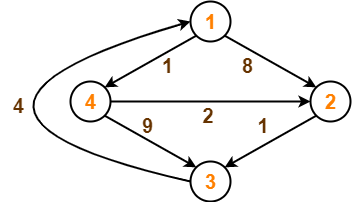
Using Floyd Warshall Algorithm, find the shortest path distance between every pair of vertices.
Solution-
Step-01:
- Remove all the self loops and parallel edges (keeping the lowest weight edge) from the graph.
- In the given graph, there are neither self edges nor parallel edges.
Step-02:
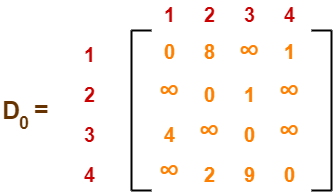
- Write the initial distance matrix.
- It represents the distance between every pair of vertices in the form of given weights.
- For diagonal elements (representing self-loops), distance value = 0.
- For vertices having a direct edge between them, distance value = weight of that edge.
- For vertices having no direct edge between them, distance value = ∞.
Initial distance matrix for the given graph is-
Step-03:
Using Floyd Warshall Algorithm, write the following 4 matrices-
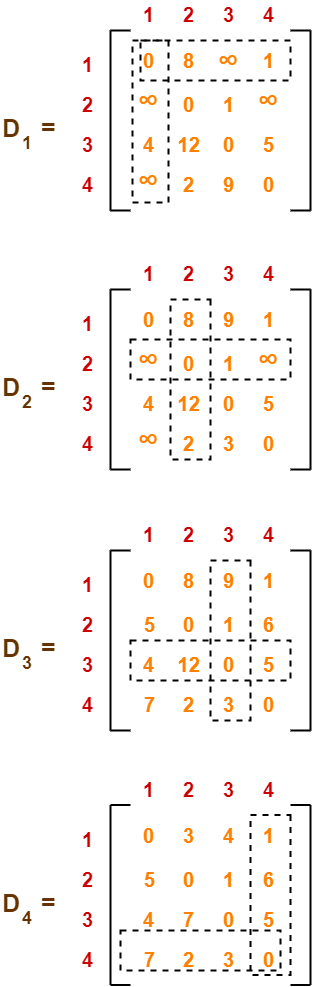
To learn how to write these matrices, watch this video here.
The last matrix D4 represents the shortest path distance between every pair of vertices.
Remember-
- In the above problem, there are 4 vertices in the given graph.
- So, there will be total 4 matrices of order 4 x 4 in the solution excluding the initial distance matrix.
- Diagonal elements of each matrix will always be 0.
To gain better understanding about Floyd Warshall Algorithm,
Next Article- Knapsack Problem
Get more notes and other study material of Design and Analysis of Algorithms.
Watch video lectures by visiting our YouTube channel LearnVidFun.