Recursion-

 

Recursion can be classified into following three types-

 

 

1. Left Recursion
2. Right Recursion
3. General Recursion

 

1. Left Recursion-

 

• A production of grammar is said to have left recursion if the leftmost variable of its RHS is same as variable of its LHS.
• A grammar containing a production having left recursion is called as Left Recursive Grammar.

 

Example-

 

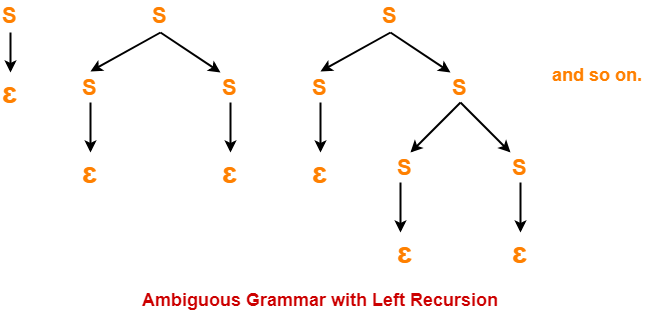
S → Sa / ∈

(Left Recursive Grammar)

 

• Left recursion is considered to be a problematic situation for Top down parsers.
• Therefore, left recursion has to be eliminated from the grammar.

 

Elimination of Left Recursion   Left recursion is eliminated by converting the grammar into a right recursive grammar.   If we have the left-recursive pair of productions- A → Aα / β (Left Recursive Grammar) where β does not begin with an A.   Then, we can eliminate left recursion by replacing the pair of productions with- A → βA’ A’ → αA’ / ∈ (Right Recursive Grammar)   This right recursive grammar functions same as left recursive grammar.

 

2. Right Recursion-

 

• A production of grammar is said to have right recursion if the rightmost variable of its RHS is same as variable of its LHS.
• A grammar containing a production having right recursion is called as Right Recursive Grammar.

 

Example-

 

S → aS / ∈

(Right Recursive Grammar)

 

• Right recursion does not create any problem for the Top down parsers.
• Therefore, there is no need of eliminating right recursion from the grammar.

 

Also Read- Types of Recursive Grammar

 

3. General Recursion-

 

• The recursion which is neither left recursion nor right recursion is called as general recursion.

 

Example-

 

S → aSb / ∈

 

PRACTICE PROBLEMS BASED ON LEFT RECURSION ELIMINATION-

 

Problem-01:

 

Consider the following grammar and eliminate left recursion-

A → ABd / Aa / a

B → Be / b

 

Solution-

 

The grammar after eliminating left recursion is-

A → aA’

A’ → BdA’ / aA’ / ∈

B → bB’

B’ → eB’ / ∈

 

Problem-02:

 

Consider the following grammar and eliminate left recursion-

E → E + E / E x E / a

 

Solution-

 

The grammar after eliminating left recursion is-

E → aA

A → +EA / xEA / ∈

 

Problem-03:

 

Consider the following grammar and eliminate left recursion-

E → E + T / T

T → T x F / F

F → id

 

Solution-

 

The grammar after eliminating left recursion is-

E → TE’

E’ → +TE’ / ∈

T → FT’

T’ → xFT’ / ∈

F → id

 

Problem-04:

 

Consider the following grammar and eliminate left recursion-

S → (L) / a

L → L , S / S

Solution-

 

The grammar after eliminating left recursion is-

S → (L) / a

L → SL’

L’ → ,SL’ / ∈

 

Problem-05:

 

Consider the following grammar and eliminate left recursion-

S → S0S1S / 01

 

Solution-

 

The grammar after eliminating left recursion is-

S → 01A

A → 0S1SA / ∈

 

Problem-06:

 

Consider the following grammar and eliminate left recursion-

S → A

A → Ad / Ae / aB / ac

B → bBc / f

 

Solution-

 

The grammar after eliminating left recursion is-

S → A

A → aBA’ / acA’

A’ → dA’ / eA’ / ∈

B → bBc / f

 

Problem-07:

 

Consider the following grammar and eliminate left recursion-

A → AAα / β

Solution-

 

The grammar after eliminating left recursion is-

A → βA’

A’ → AαA’ / ∈

 

Problem-08:

 

Consider the following grammar and eliminate left recursion-

A → Ba / Aa / c

B → Bb / Ab / d

 

Solution-

 

This is a case of indirect left recursion.

 

Step-01:

 

First let us eliminate left recursion from A → Ba / Aa / c

 

Eliminating left recursion from here, we get-

A → BaA’ / cA’

A’ → aA’ / ∈

 

Now, given grammar becomes-

A → BaA’ / cA’

A’ → aA’ / ∈

B → Bb / Ab / d

 

Step-02:

 

Substituting the productions of A in B → Ab, we get the following grammar-

A → BaA’ / cA’

A’ → aA’ / ∈

B → Bb / BaA’b / cA’b / d

 

Step-03:

 

Now, eliminating left recursion from the productions of B, we get the following grammar-

A → BaA’ / cA’

A’ → aA’ / ∈

B → cA’bB’ / dB’

B’ → bB’ / aA’bB’ / ∈

 

This is the final grammar after eliminating left recursion.

 

Problem-09:

 

Consider the following grammar and eliminate left recursion-

X → XSb / Sa / b

S → Sb / Xa / a

Solution-

 

This is a case of indirect left recursion.

 

Step-01:

 

First let us eliminate left recursion from X → XSb / Sa / b

 

Eliminating left recursion from here, we get-

X → SaX’ / bX’

X’ → SbX’ / ∈

 

Now, given grammar becomes-

X → SaX’ / bX’

X’ → SbX’ / ∈

S → Sb / Xa / a

 

Step-02:

 

Substituting the productions of X in S → Xa, we get the following grammar-

X → SaX’ / bX’

X’ → SbX’ / ∈

S → Sb / SaX’a / bX’a / a

 

Step-03:

 

Now, eliminating left recursion from the productions of S, we get the following grammar-

X → SaX’ / bX’

X’ → SbX’ / ∈

S → bX’aS’ / aS’

S’ → bS’ / aX’aS’ / ∈

 

This is the final grammar after eliminating left recursion.

 

Problem-10:

 

Consider the following grammar and eliminate left recursion-

S → Aa / b

A → Ac / Sd / ∈

Solution-

 

This is a case of indirect left recursion.

 

Step-01:

 

First let us eliminate left recursion from S → Aa / b

This is already free from left recursion.

 

Step-02:

 

Substituting the productions of S in A → Sd, we get the following grammar-

S → Aa / b

A → Ac / Aad / bd / ∈

 

Step-03:

 

Now, eliminating left recursion from the productions of A, we get the following grammar-

S → Aa / b

A → bdA’ / A’

A’ → cA’ / adA’ / ∈

 

This is the final grammar after eliminating left recursion.

 

Also Read- Left Factoring

 

To gain better understanding about Left Recursion Elimination,

Watch this Video Lecture

 

Next Article- Types of Grammars

 

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.