Decomposition in DBMS-
Before you go through this article, make sure that you have gone through the previous article on Decomposition in DBMS.
We have discussed-
- Decomposition is a process of dividing a single relation into two or more sub relations.
- Decomposition of a relation can be completed in the following two ways-

- Lossless Join Decomposition
- Lossy Join Decomposition
In this article, we will learn how to determine whether the decomposition is lossless or lossy.
Determining Whether Decomposition Is Lossless Or Lossy-
Consider a relation R is decomposed into two sub relations R1 and R2.
Then,
- If all the following conditions satisfy, then the decomposition is lossless.
- If any of these conditions fail, then the decomposition is lossy.
Condition-01:
Union of both the sub relations must contain all the attributes that are present in the original relation R.
Thus,
| R1 ∪ R2 = R |
Condition-02:
- Intersection of both the sub relations must not be null.
- In other words, there must be some common attribute which is present in both the sub relations.
Thus,
| R1 ∩ R2 ≠ ∅ |
Condition-03:
Intersection of both the sub relations must be a super key of either R1 or R2 or both.
Thus,
| R1 ∩ R2 = Super key of R1 or R2 |
PRACTICE PROBLEMS BASED ON DETERMINING WHETHER DECOMPOSITION IS LOSSLESS OR LOSSY-
Problem-01:
Consider a relation schema R ( A , B , C , D ) with the functional dependencies A → B and C → D. Determine whether the decomposition of R into R1 ( A , B ) and R2 ( C , D ) is lossless or lossy.
Solution-
To determine whether the decomposition is lossless or lossy,
- We will check all the conditions one by one.
- If any of the conditions fail, then the decomposition is lossy otherwise lossless.
Condition-01:
According to condition-01, union of both the sub relations must contain all the attributes of relation R.
So, we have-
R1 ( A , B ) ∪ R2 ( C , D )
= R ( A , B , C , D )
Clearly, union of the sub relations contain all the attributes of relation R.
Thus, condition-01 satisfies.
Condition-02:
According to condition-02, intersection of both the sub relations must not be null.
So, we have-
R1 ( A , B ) ∩ R2 ( C , D )
= Φ
Clearly, intersection of the sub relations is null.
So, condition-02 fails.
Thus, we conclude that the decomposition is lossy.
Problem-02:
Consider a relation schema R ( A , B , C , D ) with the following functional dependencies-
A → B
B → C
C → D
D → B
Determine whether the decomposition of R into R1 ( A , B ) , R2 ( B , C ) and R3 ( B , D ) is lossless or lossy.
Solution-
Strategy to Solve
When a given relation is decomposed into more than two sub relations, then-
As a thumb rule, remember- Any relation can be decomposed only into two sub relations at a time. |
Consider the original relation R was decomposed into the given sub relations as shown-
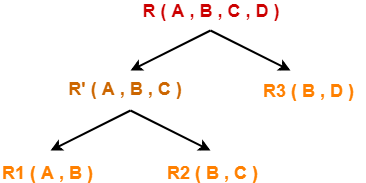
Decomposition of R(A, B, C, D) into R'(A, B, C) and R3(B, D)-
To determine whether the decomposition is lossless or lossy,
- We will check all the conditions one by one.
- If any of the conditions fail, then the decomposition is lossy otherwise lossless.
Condition-01:
According to condition-01, union of both the sub relations must contain all the attributes of relation R.
So, we have-
R‘ ( A , B , C ) ∪ R3 ( B , D )
= R ( A , B , C , D )
Clearly, union of the sub relations contain all the attributes of relation R.
Thus, condition-01 satisfies.
Condition-02:
According to condition-02, intersection of both the sub relations must not be null.
So, we have-
R‘ ( A , B , C ) ∩ R3 ( B , D )
= B
Clearly, intersection of the sub relations is not null.
Thus, condition-02 satisfies.
Condition-03:
According to condition-03, intersection of both the sub relations must be the super key of one of the two sub relations or both.
So, we have-
R‘ ( A , B , C ) ∩ R3 ( B , D )
= B
Now, the closure of attribute B is-
B+ = { B , C , D }
Now, we see-
- Attribute ‘B’ can not determine attribute ‘A’ of sub relation R’.
- Thus, it is not a super key of the sub relation R’.
- Attribute ‘B’ can determine all the attributes of sub relation R3.
- Thus, it is a super key of the sub relation R3.
Clearly, intersection of the sub relations is a super key of one of the sub relations.
So, condition-03 satisfies.
Thus, we conclude that the decomposition is lossless.
Decomposition of R'(A, B, C) into R1(A, B) and R2(B, C)-
To determine whether the decomposition is lossless or lossy,
- We will check all the conditions one by one.
- If any of the conditions fail, then the decomposition is lossy otherwise lossless.
Condition-01:
According to condition-01, union of both the sub relations must contain all the attributes of relation R’.
So, we have-
R1 ( A , B ) ∪ R2 ( B , C )
= R’ ( A , B , C )
Clearly, union of the sub relations contain all the attributes of relation R’.
Thus, condition-01 satisfies.
Condition-02:
According to condition-02, intersection of both the sub relations must not be null.
So, we have-
R1 ( A , B ) ∩ R2 ( B , C )
= B
Clearly, intersection of the sub relations is not null.
Thus, condition-02 satisfies.
Condition-03:
According to condition-03, intersection of both the sub relations must be the super key of one of the two sub relations or both.
So, we have-
R1 ( A , B ) ∩ R2 ( B , C )
= B
Now, the closure of attribute B is-
B+ = { B , C , D }
Now, we see-
- Attribute ‘B’ can not determine attribute ‘A’ of sub relation R1.
- Thus, it is not a super key of the sub relation R1.
- Attribute ‘B’ can determine all the attributes of sub relation R2.
- Thus, it is a super key of the sub relation R2.
Clearly, intersection of the sub relations is a super key of one of the sub relations.
So, condition-03 satisfies.
Thus, we conclude that the decomposition is lossless.
Conclusion-
Overall decomposition of relation R into sub relations R1, R2 and R3 is lossless.
Next Article- Introduction to Normal Forms
Get more notes and other study material of Database Management System (DBMS).
Watch video lectures by visiting our YouTube channel LearnVidFun.