Decomposition of a Relation-
| The process of breaking up or dividing a single relation into two or more sub relations is called as decomposition of a relation. |
Properties of Decomposition-
The following two properties must be followed when decomposing a given relation-
1. Lossless decomposition-
Lossless decomposition ensures-
- No information is lost from the original relation during decomposition.
- When the sub relations are joined back, the same relation is obtained that was decomposed.
Every decomposition must always be lossless.
2. Dependency Preservation-
Dependency preservation ensures-
- None of the functional dependencies that holds on the original relation are lost.
- The sub relations still hold or satisfy the functional dependencies of the original relation.
Types of Decomposition-
Decomposition of a relation can be completed in the following two ways-

1. Lossless Join Decomposition-
- Consider there is a relation R which is decomposed into sub relations R1 , R2 , …. , Rn.
- This decomposition is called lossless join decomposition when the join of the sub relations results in the same relation R that was decomposed.
- For lossless join decomposition, we always have-
| R1 ⋈ R2 ⋈ R3 ……. ⋈ Rn = R |
where ⋈ is a natural join operator
Example-
Consider the following relation R( A , B , C )-
| A | B | C |
| 1 | 2 | 1 |
| 2 | 5 | 3 |
| 3 | 3 | 3 |
R( A , B , C )
Consider this relation is decomposed into two sub relations R1( A , B ) and R2( B , C )-
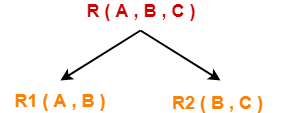
The two sub relations are-
| A | B |
| 1 | 2 |
| 2 | 5 |
| 3 | 3 |
R1( A , B )
| B | C |
| 2 | 1 |
| 5 | 3 |
| 3 | 3 |
R2( B , C )
Now, let us check whether this decomposition is lossless or not.
For lossless decomposition, we must have-
R1 ⋈ R2 = R
Now, if we perform the natural join ( ⋈ ) of the sub relations R1 and R2 , we get-
| A | B | C |
| 1 | 2 | 1 |
| 2 | 5 | 3 |
| 3 | 3 | 3 |
This relation is same as the original relation R.
Thus, we conclude that the above decomposition is lossless join decomposition.
NOTE-
- Lossless join decomposition is also known as non-additive join decomposition.
- This is because the resultant relation after joining the sub relations is same as the decomposed relation.
- No extraneous tuples appear after joining of the sub-relations.
2. Lossy Join Decomposition-
- Consider there is a relation R which is decomposed into sub relations R1 , R2 , …. , Rn.
- This decomposition is called lossy join decomposition when the join of the sub relations does not result in the same relation R that was decomposed.
- The natural join of the sub relations is always found to have some extraneous tuples.
- For lossy join decomposition, we always have-
| R1 ⋈ R2 ⋈ R3 ……. ⋈ Rn ⊃ R |
where ⋈ is a natural join operator
Example-
Consider the following relation R( A , B , C )-
| A | B | C |
| 1 | 2 | 1 |
| 2 | 5 | 3 |
| 3 | 3 | 3 |
R( A , B , C )
Consider this relation is decomposed into two sub relations as R1( A , C ) and R2( B , C )-
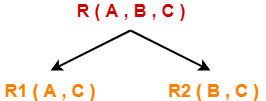
The two sub relations are-
| A | C |
| 1 | 1 |
| 2 | 3 |
| 3 | 3 |
R1( A , B )
| B | C |
| 2 | 1 |
| 5 | 3 |
| 3 | 3 |
R2( B , C )
Now, let us check whether this decomposition is lossy or not.
For lossy decomposition, we must have-
R1 ⋈ R2 ⊃ R
Now, if we perform the natural join ( ⋈ ) of the sub relations R1 and R2 we get-
| A | B | C |
| 1 | 2 | 1 |
| 2 | 5 | 3 |
| 2 | 3 | 3 |
| 3 | 5 | 3 |
| 3 | 3 | 3 |
This relation is not same as the original relation R and contains some extraneous tuples.
Clearly, R1 ⋈ R2 ⊃ R.
Thus, we conclude that the above decomposition is lossy join decomposition.
NOTE-
- Lossy join decomposition is also known as careless decomposition.
- This is because extraneous tuples get introduced in the natural join of the sub-relations.
- Extraneous tuples make the identification of the original tuples difficult.
Next Article- Rules to Determine Lossless and Lossy Decomposition
Get more notes and other study material of Database Management System (DBMS).
Watch video lectures by visiting our YouTube channel LearnVidFun.

