Master Theorem-
| Master’s Theorem is a popular method for solving the recurrence relations. |
Master’s theorem solves recurrence relations of the form-
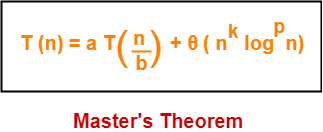
Here, a >= 1, b > 1, k >= 0 and p is a real number.
Master Theorem Cases-
To solve recurrence relations using Master’s theorem, we compare a with bk.
Then, we follow the following cases-
Case-01:
If a > bk, then T(n) = θ (nlogba)
Case-02:
If a = bk and
- If p < -1, then T(n) = θ (nlogba)
- If p = -1, then T(n) = θ (nlogba.log2n)
- If p > -1, then T(n) = θ (nlogba.logp+1n)
Case-03:
If a < bk and
- If p < 0, then T(n) = O (nk)
- If p >= 0, then T(n) = θ (nklogpn)
PRACTICE PROBLEMS BASED ON MASTER THEOREM-
Problem-01:
Solve the following recurrence relation using Master’s theorem-
T(n) = 3T(n/2) + n2
Solution-
We compare the given recurrence relation with T(n) = aT(n/b) + θ (nklogpn).
Then, we have-
a = 3
b = 2
k = 2
p = 0
Now, a = 3 and bk = 22 = 4.
Clearly, a < bk.
So, we follow case-03.
Since p = 0, so we have-
T(n) = θ (nklogpn)
T(n) = θ (n2log0n)
Thus,
| T(n) = θ (n2) |
Problem-02:
Solve the following recurrence relation using Master’s theorem-
T(n) = 2T(n/2) + nlogn
Solution-
We compare the given recurrence relation with T(n) = aT(n/b) + θ (nklogpn).
Then, we have-
a = 2
b = 2
k = 1
p = 1
Now, a = 2 and bk = 21 = 2.
Clearly, a = bk.
So, we follow case-02.
Since p = 1, so we have-
T(n) = θ (nlogba.logp+1n)
T(n) = θ (nlog22.log1+1n)
Thus,
| T(n) = θ (nlog2n) |
Problem-03:
Solve the following recurrence relation using Master’s theorem-
T(n) = 2T(n/4) + n0.51
Solution-
We compare the given recurrence relation with T(n) = aT(n/b) + θ (nklogpn).
Then, we have-
a = 2
b = 4
k = 0.51
p = 0
Now, a = 2 and bk = 40.51 = 2.0279.
Clearly, a < bk.
So, we follow case-03.
Since p = 0, so we have-
T(n) = θ (nklogpn)
T(n) = θ (n0.51log0n)
Thus,
| T(n) = θ (n0.51) |
Problem-04:
Solve the following recurrence relation using Master’s theorem-
T(n) = √2T(n/2) + logn
Solution-
We compare the given recurrence relation with T(n) = aT(n/b) + θ (nklogpn).
Then, we have-
a = √2
b = 2
k = 0
p = 1
Now, a = √2 = 1.414 and bk = 20 = 1.
Clearly, a > bk.
So, we follow case-01.
So, we have-
T(n) = θ (nlogba)
T(n) = θ (nlog2√2)
T(n) = θ (n1/2)
Thus,
| T(n) = θ (√n) |
Problem-05:
Solve the following recurrence relation using Master’s theorem-
T(n) = 8T(n/4) – n2logn
Solution-
- The given recurrence relation does not correspond to the general form of Master’s theorem.
- So, it can not be solved using Master’s theorem.
Problem-06:
Solve the following recurrence relation using Master’s theorem-
T(n) = 3T(n/3) + n/2
Solution-
- We write the given recurrence relation as T(n) = 3T(n/3) + n.
- This is because in the general form, we have θ for function f(n) which hides constants in it.
- Now, we can easily apply Master’s theorem.
We compare the given recurrence relation with T(n) = aT(n/b) + θ (nklogpn).
Then, we have-
a = 3
b = 3
k = 1
p = 0
Now, a = 3 and bk = 31 = 3.
Clearly, a = bk.
So, we follow case-02.
Since p = 0, so we have-
T(n) = θ (nlogba.logp+1n)
T(n) = θ (nlog33.log0+1n)
T(n) = θ (n1.log1n)
Thus,
| T(n) = θ (nlogn) |
Problem-07:
Form a recurrence relation for the following code and solve it using Master’s theorem-
A(n)
{
if(n<=1)
return 1;
else
return A(√n);
}
Solution-
- We write a recurrence relation for the given code as T(n) = T(√n) + 1.
- Here 1 = Constant time taken for comparing and returning the value.
- We can not directly apply Master’s Theorem on this recurrence relation.
- This is because it does not correspond to the general form of Master’s theorem.
- However, we can modify and bring it in the general form to apply Master’s theorem.
Let-
n = 2m ……(1)
Then-
T(2m) = T(2m/2) + 1
Now, let T(2m) = S(m), then T(2m/2) = S(m/2)
So, we have-
S(m) = S(m/2) +1
Now, we can easily apply Master’s Theorem.
We compare the given recurrence relation with S(m) = aS(m/b) + θ (mklogpm).
Then, we have-
a = 1
b = 2
k = 0
p = 0
Now, a = 1 and bk = 20 = 1.
Clearly, a = bk.
So, we follow case-02.
Since p = 0, so we have-
S(m) = θ (mlogba.logp+1m)
S(m) = θ (mlog21.log0+1m)
S(m) = θ (m0.log1m)
Thus,
S(m) = θ(logm) ……(2)
Now,
- From (1), we have n = 2m.
- So, logn = mlog2 which implies m = log2n.
Substituting in (2), we get-
S(m) = θ(loglog2n)
Or
| T(n) = θ (loglog2n) |
To gain better understanding about Master’s Theorem,
Next Article- Recursion Tree
Get more notes and other study material of Design and Analysis of Algorithms.
Watch video lectures by visiting our YouTube channel LearnVidFun.