Recursion Tree | Solving Recurrence Relations

Recursion Tree-

 

• Like Master’s Theorem, Recursion Tree is another method for solving the recurrence relations.
• A recursion tree is a tree where each node represents the cost of a certain recursive sub-problem.
• We sum up the values in each node to get the cost of the entire algorithm.

 

Steps to Solve Recurrence Relations Using Recursion Tree Method-

 

Step-01:

 

Draw a recursion tree based on the given recurrence relation.

 

Step-02:

 

Determine-

• Cost of each level
• Total number of levels in the recursion tree
• Number of nodes in the last level
• Cost of the last level

 

Step-03:

 

Add cost of all the levels of the recursion tree and simplify the expression so obtained in terms of asymptotic notation.

 

Following problems clearly illustrates how to apply these steps.

 

PRACTICE PROBLEMS BASED ON RECURSION TREE-

 

Problem-01:

 

Solve the following recurrence relation using recursion tree method-

T(n) = 2T(n/2) + n

 

Solution-

 

Step-01:

 

Draw a recursion tree based on the given recurrence relation.

 

The given recurrence relation shows-

• A problem of size n will get divided into 2 sub-problems of size n/2.
• Then, each sub-problem of size n/2 will get divided into 2 sub-problems of size n/4 and so on.
• At the bottom most layer, the size of sub-problems will reduce to 1.

 

This is illustrated through following recursion tree-

 

 

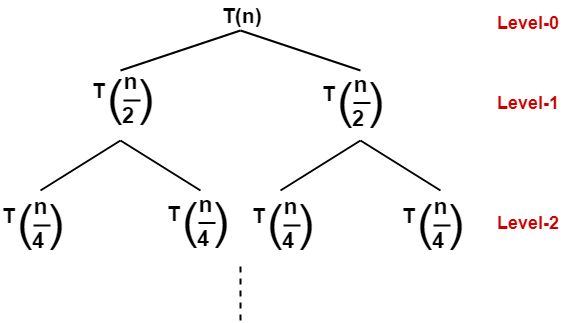
The given recurrence relation shows-

• The cost of dividing a problem of size n into its 2 sub-problems and then combining its solution is n.
• The cost of dividing a problem of size n/2 into its 2 sub-problems and then combining its solution is n/2 and so on.

 

This is illustrated through following recursion tree where each node represents the cost of the corresponding sub-problem-

 

 

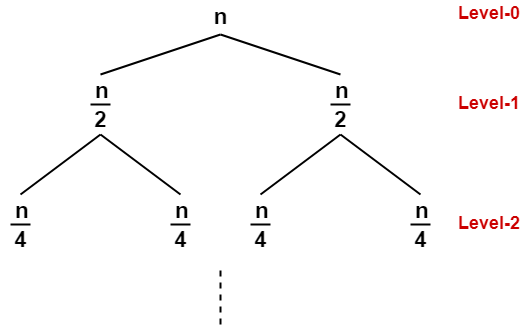
Step-02:

 

Determine cost of each level-

• Cost of level-0 = n
• Cost of level-1 = n/2 + n/2 = n
• Cost of level-2 = n/4 + n/4 + n/4 + n/4 = n and so on.

 

Step-03:

 

Determine total number of levels in the recursion tree-

• Size of sub-problem at level-0 = n/2⁰
• Size of sub-problem at level-1 = n/2¹
• Size of sub-problem at level-2 = n/2²

 

Continuing in similar manner, we have-

Size of sub-problem at level-i = n/2ⁱ

Suppose at level-x (last level), size of sub-problem becomes 1. Then-

n / 2^x = 1

2^x = n

Taking log on both sides, we get-

xlog2 = logn

x = log₂n

 

∴ Total number of levels in the recursion tree = log₂n + 1

 

Step-04:

 

Determine number of nodes in the last level-

• Level-0 has 2⁰ nodes i.e. 1 node
• Level-1 has 2¹ nodes i.e. 2 nodes
• Level-2 has 2² nodes i.e. 4 nodes

 

Continuing in similar manner, we have-

Level-log₂n has 2^log₂n nodes i.e. n nodes

 

Step-05:

 

Determine cost of last level-

Cost of last level = n x T(1) = θ(n)

 

Step-06:

 

Add costs of all the levels of the recursion tree and simplify the expression so obtained in terms of asymptotic notation-

 

 

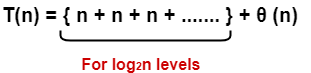
= n x log₂n + θ (n)

= nlog₂n + θ (n)

= θ (nlog₂n)

 

Problem-02:

 

Solve the following recurrence relation using recursion tree method-

T(n) = T(n/5) + T(4n/5) + n

 

Solution-

 

Step-01:

 

Draw a recursion tree based on the given recurrence relation.

 

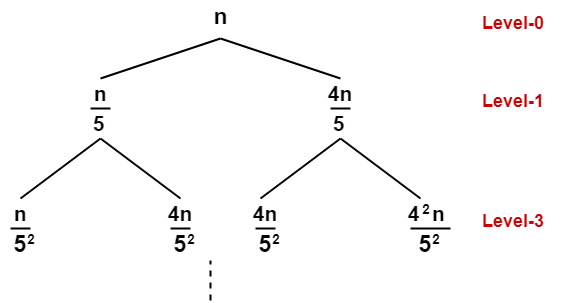
The given recurrence relation shows-

• A problem of size n will get divided into 2 sub-problems- one of size n/5 and another of size 4n/5.
• Then, sub-problem of size n/5 will get divided into 2 sub-problems- one of size n/5² and another of size 4n/5².
• On the other side, sub-problem of size 4n/5 will get divided into 2 sub-problems- one of size 4n/5² and another of size 4²n/5² and so on.
• At the bottom most layer, the size of sub-problems will reduce to 1.

 

This is illustrated through following recursion tree-

 

 

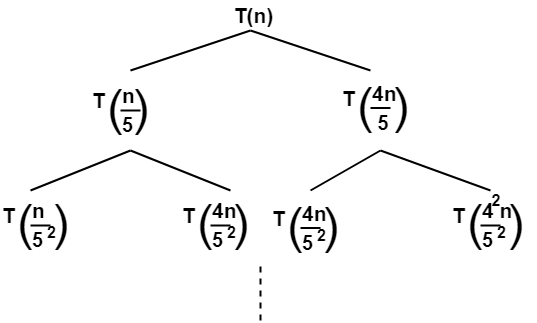
The given recurrence relation shows-

• The cost of dividing a problem of size n into its 2 sub-problems and then combining its solution is n.
• The cost of dividing a problem of size n/5 into its 2 sub-problems and then combining its solution is n/5.
• The cost of dividing a problem of size 4n/5 into its 2 sub-problems and then combining its solution is 4n/5 and so on.

 

This is illustrated through following recursion tree where each node represents the cost of the corresponding sub-problem-

 

 

Step-02:

 

Determine cost of each level-

• Cost of level-0 = n
• Cost of level-1 = n/5 + 4n/5 = n
• Cost of level-2 = n/5² + 4n/5² + 4n/5² + 4²n/5² = n

 

Step-03:

 

Determine total number of levels in the recursion tree. We will consider the rightmost sub tree as it goes down to the deepest level-

• Size of sub-problem at level-0 = (4/5)⁰n
• Size of sub-problem at level-1 =(4/5)¹n
• Size of sub-problem at level-2 =(4/5)²n

 

Continuing in similar manner, we have-

Size of sub-problem at level-i = (4/5)ⁱn

Suppose at level-x (last level), size of sub-problem becomes 1. Then-

(4/5)^xn = 1

(4/5)^x = 1/n

Taking log on both sides, we get-

xlog(4/5) = log(1/n)

x = log_5/4n

 

∴ Total number of levels in the recursion tree = log_5/4n + 1

 

Step-04:

 

Determine number of nodes in the last level-

• Level-0 has 2⁰ nodes i.e. 1 node
• Level-1 has 2¹ nodes i.e. 2 nodes
• Level-2 has 2² nodes i.e. 4 nodes

 

Continuing in similar manner, we have-

Level-log_5/4n has 2^log_5/4n nodes

 

Step-05:

 

Determine cost of last level-

Cost of last level = 2^log_5/4n x T(1) = θ(2^log_5/4n) = θ(n^log_5/42)

 

Step-06:

 

Add costs of all the levels of the recursion tree and simplify the expression so obtained in terms of asymptotic notation-

 

 

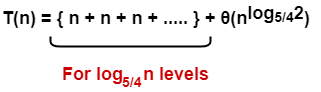
= nlog_5/4n + θ(n^log_5/42)

= θ(nlog_5/4n)

 

Problem-03:

 

Solve the following recurrence relation using recursion tree method-

T(n) = 3T(n/4) + cn²

 

Solution-

 

Step-01:

 

Draw a recursion tree based on the given recurrence relation-

 

 

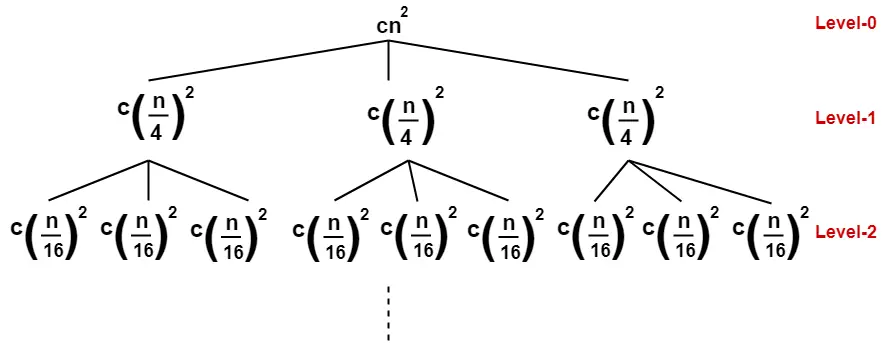
(Here, we have directly drawn a recursion tree representing the cost of sub problems)

 

Step-02:

 

Determine cost of each level-

• Cost of level-0 = cn²
• Cost of level-1 = c(n/4)² + c(n/4)² + c(n/4)² = (3/16)cn²
• Cost of level-2 = c(n/16)² x 9 = (9/16²)cn²

 

Step-03:

 

Determine total number of levels in the recursion tree-

• Size of sub-problem at level-0 = n/4⁰
• Size of sub-problem at level-1 = n/4¹
• Size of sub-problem at level-2 = n/4²

 

Continuing in similar manner, we have-

Size of sub-problem at level-i = n/4ⁱ

Suppose at level-x (last level), size of sub-problem becomes 1. Then-

n/4^x = 1

4^x = n

Taking log on both sides, we get-

xlog4 = logn

x = log₄n

 

∴ Total number of levels in the recursion tree = log₄n + 1

 

Step-04:

 

Determine number of nodes in the last level-

• Level-0 has 3⁰ nodes i.e. 1 node
• Level-1 has 3¹ nodes i.e. 3 nodes
• Level-2 has 3² nodes i.e. 9 nodes

 

Continuing in similar manner, we have-

Level-log₄n has 3^log₄n nodes i.e. n^log₄3 nodes

 

Step-05:

 

Determine cost of last level-

Cost of last level = n^log₄3 x T(1) = θ(n^log₄3)

 

Step-06:

 

Add costs of all the levels of the recursion tree and simplify the expression so obtained in terms of asymptotic notation-

 

 

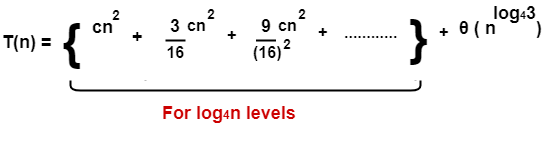
= cn² { 1 + (3/16) + (3/16)² + ……… } + θ(n^log₄3)

 

Now, { 1 + (3/16) + (3/16)² + ……… } forms an infinite Geometric progression.

 

On solving, we get-

= (16/13)cn² { 1 – (3/16)^log₄n } + θ(n^log₄3)

= (16/13)cn² – (16/13)cn² (3/16)^log₄n + θ(n^log₄3)

= O(n²)

 

To gain better understanding about Recursion Tree,

Watch this Video Lecture

 

Next Article- DFS Algorithm

 

Get more notes and other study material of Design and Analysis of Algorithms.

Watch video lectures by visiting our YouTube channel LearnVidFun.