Tag: Set Associative Cache

Set Associative Mapping | Practice Problems

Computer Organization and Architecture

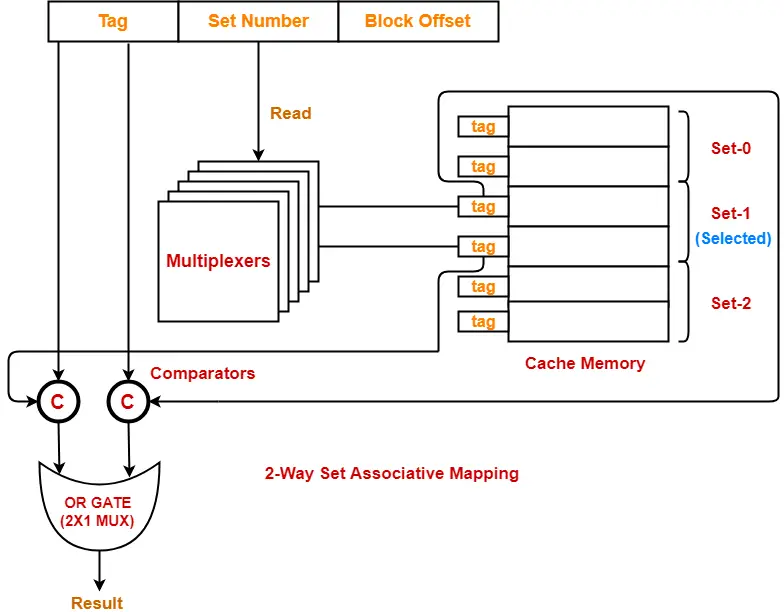
Set Associative Mapping-

 

Before you go through this article, make sure that you have gone through the previous article on Set Associative Mapping.

 

In set associative mapping,

  • A particular block of main memory can be mapped to one particular cache set only.
  • Block ‘j’ of main memory will map to set number (j mod number of sets in cache) of the cache.
  • A replacement algorithm is needed if the cache is full.

 

In this article, we will discuss practice problems based on set associative mapping.

 

Also Read- Cache Mapping Techniques

 

PRACTICE PROBLEMS BASED ON SET ASSOCIATIVE MAPPING-

 

Problem-01:

 

Consider a 2-way set associative mapped cache of size 16 KB with block size 256 bytes. The size of main memory is 128 KB. Find-

  1. Number of bits in tag
  2. Tag directory size

 

Solution-

 

Given-

  • Set size = 2
  • Cache memory size = 16 KB
  • Block size = Frame size = Line size = 256 bytes
  • Main memory size = 128 KB

 

We consider that the memory is byte addressable.

 

Number of Bits in Physical Address-

 

We have,

Size of main memory

= 128 KB

= 217 bytes

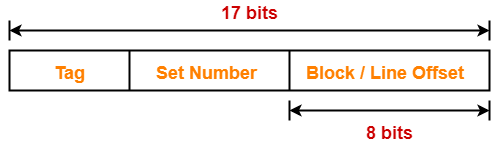
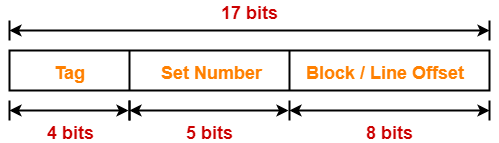
Thus, Number of bits in physical address = 17 bits

 

 

Number of Bits in Block Offset-

 

We have,

Block size

= 256 bytes

= 28 bytes

Thus, Number of bits in block offset = 8 bits

 

 

Number of Lines in Cache-

 

Total number of lines in cache

= Cache size / Line size

= 16 KB / 256 bytes

= 214 bytes / 28 bytes

= 64 lines

Thus, Number of lines in cache = 64 lines

 

Number of Sets in Cache-

 

Total number of sets in cache

= Total number of lines in cache / Set size

= 64 / 2

= 32 sets

= 25 sets

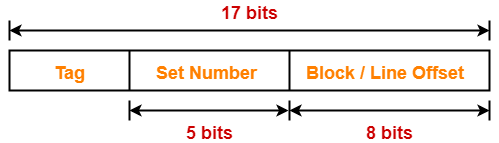
Thus, Number of bits in set number = 5 bits

 

 

Number of Bits in Tag-

 

Number of bits in tag

= Number of bits in physical address – (Number of bits in set number + Number of bits in block offset)

= 17 bits – (5 bits + 8 bits)

= 17 bits – 13 bits

= 4 bits

Thus, Number of bits in tag = 4 bits

 

 

Tag Directory Size-

 

Tag directory size

= Number of tags x Tag size

= Number of lines in cache x Number of bits in tag

= 64 x 4 bits

= 256 bits

= 32 bytes

Thus, size of tag directory = 32 bytes

 

Also Read- Practice Problems On Direct Mapping

 

Problem-02:

 

Consider a 8-way set associative mapped cache of size 512 KB with block size 1 KB. There are 7 bits in the tag. Find-

  1. Size of main memory
  2. Tag directory size

 

Solution-

 

Given-

  • Set size = 8
  • Cache memory size = 512 KB
  • Block size = Frame size = Line size = 1 KB
  • Number of bits in tag = 7 bits

 

We consider that the memory is byte addressable.

 

Number of Bits in Block Offset-

 

We have,

Block size

= 1 KB

= 210 bytes

Thus, Number of bits in block offset = 10 bits

 

 

Number of Lines in Cache-

 

Total number of lines in cache

= Cache size / Line size

= 512 KB / 1 KB

= 512 lines

Thus, Number of lines in cache = 512 lines

 

Number of Sets in Cache-

 

Total number of sets in cache

= Total number of lines in cache / Set size

= 512 / 8

= 64 sets

= 26 sets

Thus, Number of bits in set number = 6 bits

 

 

Number of Bits in Physical Address-

 

Number of bits in physical address

= Number of bits in tag + Number of bits in set number + Number of bits in block offset

= 7 bits + 6 bits + 10 bits

= 23 bits

Thus, Number of bits in physical address = 23 bits

 

Size of Main Memory-

 

We have,

Number of bits in physical address = 23 bits

Thus, Size of main memory

= 223 bytes

= 8 MB

 

Tag Directory Size-

 

Tag directory size

= Number of tags x Tag size

= Number of lines in cache x Number of bits in tag

= 512 x 7 bits

= 3584 bits

= 448 bytes

Thus, size of tag directory = 448 bytes

 

Problem-03:

 

Consider a 4-way set associative mapped cache with block size 4 KB. The size of main memory is 16 GB and there are 10 bits in the tag. Find-

  1. Size of cache memory
  2. Tag directory size

 

Solution-

 

Given-

  • Set size = 4
  • Block size = Frame size = Line size = 4 KB
  • Main memory size = 16 GB
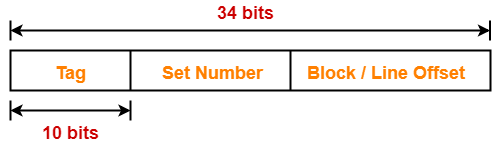
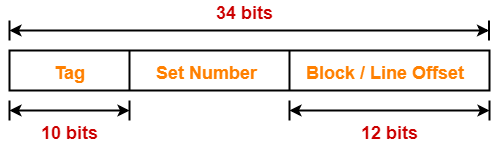
  • Number of bits in tag = 10 bits

 

We consider that the memory is byte addressable.

 

Number of Bits in Physical Address-

 

We have,

Size of main memory

= 16 GB

= 234 bytes

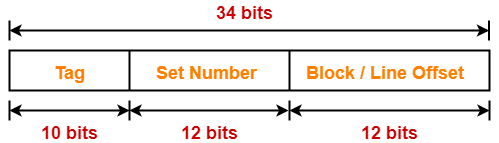
Thus, Number of bits in physical address = 34 bits

 

 

Number of Bits in Block Offset-

 

We have,

Block size

= 4 KB

= 212 bytes

Thus, Number of bits in block offset = 12 bits

 

 

Number of Bits in Set Number-

 

Number of bits in set number

= Number of bits in physical address – (Number of bits in tag + Number of bits in block offset)

= 34 bits – (10 bits + 12 bits)

= 34 bits – 22 bits

= 12 bits

Thus, Number of bits in set number = 12 bits

 

 

Number of Sets in Cache-

 

We have-

Number of bits in set number = 12 bits

Thus, Total number of sets in cache = 212 sets

 

Number of Lines in Cache-

 

We have-

Total number of sets in cache = 212 sets

Each set contains 4 lines

 

Thus,

Total number of lines in cache

= Total number of sets in cache x Number of lines in each set

= 212 x 4 lines

= 214 lines

 

Size of Cache Memory-

 

Size of cache memory

= Total number of lines in cache x Line size

= 214 x 4 KB

= 216 KB

= 64 MB

Thus, Size of cache memory = 64 MB

 

Tag Directory Size-

 

Tag directory size

= Number of tags x Tag size

= Number of lines in cache x Number of bits in tag

= 214 x 10 bits

= 163840 bits

= 20480 bytes

= 20 KB

Thus, size of tag directory = 20 KB

 

Also Read- Practice Problems On Fully Associative Mapping

 

Problem-04:

 

Consider a 8-way set associative mapped cache. The size of cache memory is 512 KB and there are 10 bits in the tag. Find the size of main memory.

 

Solution-

 

Given-

  • Set size = 8
  • Cache memory size = 512 KB
  • Number of bits in tag = 10 bits

 

We consider that the memory is byte addressable.

Let-

  • Number of bits in set number field = x bits
  • Number of bits in block offset field = y bits

 

 

Sum of Number Of Bits Of Set Number Field And Block Offset Field-

 

We have,

Cache memory size = Number of sets in cache x Number of lines in one set x Line size

Now, substituting the values, we get-

512 KB = 2x x 8 x 2y bytes

219 bytes = 23+x+y bytes

19 = 3 +x + y

x + y = 19 – 3

x + y = 16

 

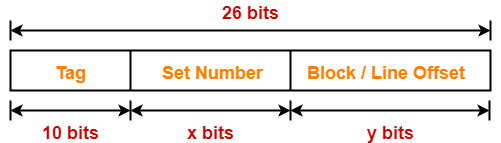
Number of Bits in Physical Address-

 

Number of bits in physical address

= Number of bits in tag + Number of bits in set number + Number of bits in block offset

= 10 bits + x bits + y bits

= 10 bits + (x + y) bits

= 10 bits + 16 bits

= 26 bits

Thus, Number of bits in physical address = 26 bits

 

 

Size of Main Memory-

 

We have,

Number of bits in physical address = 26 bits

Thus, Size of main memory

= 226 bytes

= 64 MB

Thus, size of main memory = 64 MB

 

Problem-05:

 

Consider a 4-way set associative mapped cache. The size of main memory is 64 MB and there are 10 bits in the tag. Find the size of cache memory.

 

Solution-

 

Given-

  • Set size = 4
  • Main memory size = 64 MB
  • Number of bits in tag = 10 bits

 

We consider that the memory is byte addressable.

 

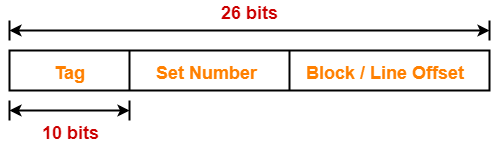
Number of Bits in Physical Address-

 

We have,

Size of main memory

= 64 MB

= 226 bytes

Thus, Number of bits in physical address = 26 bits

 

 

Sum Of Number Of Bits Of Set Number Field And Block Offset Field-

 

Let-

  • Number of bits in set number field = x bits
  • Number of bits in block offset field = y bits

 

 

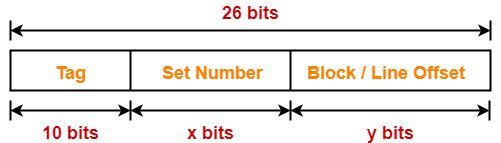
Then, Number of bits in physical address

= Number of bits in tag + Number of bits in set number + Number of bits in block offset

 

So, we have-

26 bits = 10 bits + x bits + y bits

26 = 10 + (x + y)

x + y = 26 – 10

x + y = 16

Thus, Sum of number of bits of set number field and block offset field = 16 bits

 

Size of Cache Memory-

 

Cache memory size

= Number of sets in cache x Number of lines in one set x Line size

= 2x x 4 x 2y bytes

= 22+x+y bytes

= 22+16 bytes

= 218 bytes

= 256 KB

Thus, size of cache memory = 256 KB

 

To watch video solutions and practice more problems,

Watch this Video Lecture

 

Next Article- Miscellaneous Practice Problems On Cache Mapping Techniques

 

Get more notes and other study material of Computer Organization and Architecture.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Set Associative Mapping | Set Associative Cache

Computer Organization and Architecture

Cache Mapping-

 

Before you go through this article, make sure that you have gone through the previous article on Cache Mapping.

 

Cache mapping is a technique by which the contents of main memory are brought into the cache memory.

 

Different cache mapping techniques are-

 

 

  1. Direct Mapping
  2. Fully Associative Mapping
  3. K-way Set Associative Mapping

 

In this article, we will discuss about set associative mapping in detail.

 

Set Associative Mapping-

 

In k-way set associative mapping,

  • Cache lines are grouped into sets where each set contains k number of lines.
  • A particular block of main memory can map to only one particular set of the cache.
  • However, within that set, the memory block can map to any freely available cache line.
  • The set of the cache to which a particular block of the main memory can map is given by-

 

Cache set number

= ( Main Memory Block Address ) Modulo (Number of sets in Cache)

 

Division of Physical Address-

 

In set associative mapping, the physical address is divided as-

 

 

Set Associative Cache-

 

Set associative cache employs set associative cache mapping technique.

 

The following steps explain the working of set associative cache-

 

After CPU generates a memory request,

  • The set number field of the address is used to access the particular set of the cache.
  • The tag field of the CPU address is then compared with the tags of all k lines within that set.
  • If the CPU tag matches to the tag of any cache line, a cache hit occurs.
  • If the CPU tag does not match to the tag of any cache line, a cache miss occurs.
  • In case of a cache miss, the required word has to be brought from the main memory.
  • If the cache is full, a replacement is made in accordance with the employed replacement policy.

 

Implementation-

 

The following diagram shows the implementation of 2-way set associative cache-

 

(For simplicity, this diagram shows does not show all the lines of multiplexers)

 

The steps involved are as follows-

 

Step-01:

 

  • Each multiplexer reads the set number from the generated physical address using its select lines in parallel.
  • To read the set number of S bits, number of select lines each multiplexer must have = S.

 

Step-02:

 

  • After reading the set number, each multiplexer goes to the corresponding set in the cache memory.
  • Then, each multiplexer goes to the lines of that set using its input lines in parallel.
  • Number of input lines each multiplexer must have = Number of lines in one set

 

Step-03:

 

  • Each multiplexer outputs the tag bit it has selected from the lines of selected set to the comparators using its output line.
  • Number of output line in each multiplexer = 1.

 

UNDERSTAND

 

It is important to understand-

  • A multiplexer can output only a single bit on output line.
  • So, to output one complete tag to the comparator,

Number of multiplexers required = Number of bits in the tag

  • If there are k lines in one set, then number of tags to output = k, thus-

Number of multiplexers required = Number of lines in one set (k) x Number of bits in the tag

  • Each multiplexer is configured to read the tag bit of specific line at specific location.
  • So, each multiplexer selects the tag bit for which it has been configured and outputs on the output line.
  • The complete tags as whole are sent to the comparators for comparison in parallel.

 

Step-04:

 

  • Comparators compare the tags coming from the multiplexers with the tag of the generated address.
  • This comparison takes place in parallel.
  • If there are k lines in one set (thus k tags), then-

Number of comparators required = k

and

Size of each comparator = Number of bits in the tag

  • The output result of each comparator is fed as an input to an OR Gate.
  • OR Gate is usually implemented using 2 x 1 multiplexer.
  • If the output of OR Gate is 1, a cache hit occurs otherwise a cache miss occurs.

 

Hit latency-

 

  • The time taken to find out whether the required word is present in the Cache Memory or not is called as hit latency.

 

For set associative mapping,

Hit latency = Multiplexer latency + Comparator latency + OR Gate latency

 

Also Read- Direct Mapped Cache | Implementation & Formulas

 

Important Results-

 

Following are the few important results for set associative cache-

  • Block j of main memory maps to set number (j mod number of sets in cache) of the cache.
  • Number of multiplexers required = Number of lines in one set (k) x Number of bits in tag
  • Size of each multiplexer = Number of lines in one set (k) x 1
  • Number of comparators required = Number of lines in one set (k)
  • Size of each comparator = Number of bits in the tag
  • Hit latency = Multiplexer latency + Comparator latency + OR Gate latency

 

To gain better understanding about set associative mapping,

Watch this Video Lecture

 

Next Article- Practice Problems On Set Associative Mapping

 

Get more notes and other study material of Computer Organization and Architecture.

Watch video lectures by visiting our YouTube channel LearnVidFun.