Month: April 2018

ER Diagrams to Tables

Database Management System

Converting ER Diagrams to Tables-

 

After designing an ER Diagram,

  • ER diagram is converted into the tables in relational model.
  • This is because relational models can be easily implemented by RDBMS like MySQL , Oracle etc.

 

Following rules are used for converting an ER diagram into the tables-

 

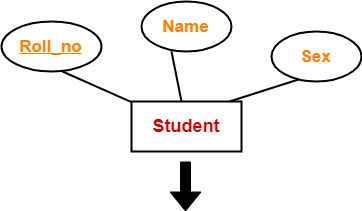
Rule-01: For Strong Entity Set With Only Simple Attributes-

 

A strong entity set with only simple attributes will require only one table in relational model.

  • Attributes of the table will be the attributes of the entity set.
  • The primary key of the table will be the key attribute of the entity set.

 

Example-

 

 

Roll_no Name Sex
 

 

 

Schema : Student ( Roll_no , Name , Sex )

 

Also Read- Entity Sets in DBMS

 

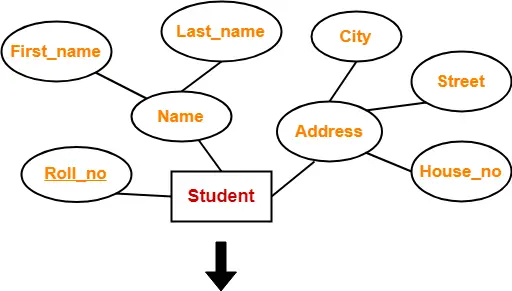
Rule-02: For Strong Entity Set With Composite Attributes-

 

  • A strong entity set with any number of composite attributes will require only one table in relational model.
  • While conversion, simple attributes of the composite attributes are taken into account and not the composite attribute itself.

 

Example-

 

 

Roll_no First_name Last_name House_no Street City
 

 

 

 

Schema : Student ( Roll_no , First_name , Last_name , House_no , Street , City )

 

Also Read- Types of Attributes in DBMS

 

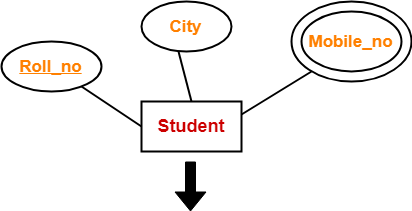
Rule-03: For Strong Entity Set With Multi Valued Attributes-

 

A strong entity set with any number of multi valued attributes will require two tables in relational model.

  • One table will contain all the simple attributes with the primary key.
  • Other table will contain the primary key and all the multi valued attributes.

 

Example-

 

 

Roll_no City
 

 

 

Roll_no Mobile_no
 

 

 

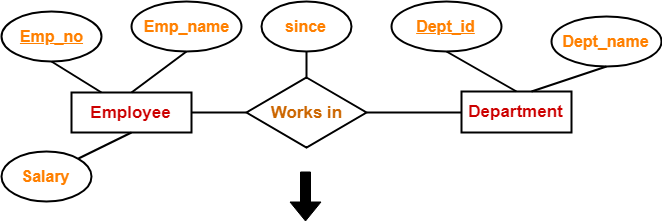
Rule-04: Translating Relationship Set into a Table-

 

A relationship set will require one table in the relational model.

Attributes of the table are-

  • Primary key attributes of the participating entity sets
  • Its own descriptive attributes if any.

Set of non-descriptive attributes will be the primary key.

 

Example-

 

 

Emp_no Dept_id since
 

 

Schema : Works in ( Emp_no , Dept_id , since )

 

NOTE-

 

If we consider the overall ER diagram, three tables will be required in relational model-

  • One table for the entity set “Employee”
  • One table for the entity set “Department”
  • One table for the relationship set “Works in”

 

Rule-05: For Binary Relationships With Cardinality Ratios-

 

The following four cases are possible-

 

Case-01: Binary relationship with cardinality ratio m:n

Case-02: Binary relationship with cardinality ratio 1:n

Case-03: Binary relationship with cardinality ratio m:1

Case-04: Binary relationship with cardinality ratio 1:1

 

Also read- Cardinality Ratios in DBMS

 

Case-01: For Binary Relationship With Cardinality Ratio m:n

 

 

Here, three tables will be required-

  1. A ( a1 , a2 )
  2. R ( a1 , b1 )
  3. B ( b1 , b2 )

 

Case-02: For Binary Relationship With Cardinality Ratio 1:n

 

 

Here, two tables will be required-

  1. A ( a1 , a2 )
  2. BR ( a1 , b1 , b2 )

 

NOTE- Here, combined table will be drawn for the entity set B and relationship set R.

 

Case-03: For Binary Relationship With Cardinality Ratio m:1

 

 

Here, two tables will be required-

  1. AR ( a1 , a2 , b1 )
  2. B ( b1 , b2 )

 

NOTE- Here, combined table will be drawn for the entity set A and relationship set R.

 

Case-04: For Binary Relationship With Cardinality Ratio 1:1

 

 

Here, two tables will be required. Either combine ‘R’ with ‘A’ or ‘B’

 

Way-01:

  1. AR ( a1 , a2 , b1 )
  2. B ( b1 , b2 )

 

Way-02:

  1. A ( a1 , a2 )
  2. BR ( a1 , b1 , b2 )

 

Thumb Rules to Remember

 

While determining the minimum number of tables required for binary relationships with given cardinality ratios, following thumb rules must be kept in mind-

  • For binary relationship with cardinality ration m : n , separate and individual tables will be drawn for each entity set and relationship.
  • For binary relationship with cardinality ratio either m : 1 or 1 : n , always remember “many side will consume the relationship” i.e. a combined table will be drawn for many side entity set and relationship set.
  • For binary relationship with cardinality ratio 1 : 1 , two tables will be required. You can combine the relationship set with any one of the entity sets.

 

Rule-06: For Binary Relationship With Both Cardinality Constraints and Participation Constraints-

 

  • Cardinality constraints will be implemented as discussed in Rule-05.
  • Because of the total participation constraint, foreign key acquires NOT NULL constraint i.e. now foreign key can not be null.

 

Case-01: For Binary Relationship With Cardinality Constraint and Total Participation Constraint From One Side-

 

 

Because cardinality ratio = 1 : n , so we will combine the entity set B and relationship set R.

Then, two tables will be required-

  1. A ( a1 , a2 )
  2. BR ( a1 , b1 , b2 )

Because of total participation, foreign key a1 has acquired NOT NULL constraint, so it can’t be null now.

 

Case-02: For Binary Relationship With Cardinality Constraint and Total Participation Constraint From Both Sides-

 

If there is a key constraint from both the sides of an entity set with total participation, then that binary relationship is represented using only single table.

 

 

Here, Only one table is required.

  • ARB ( a1 , a2 , b1 , b2 )

 

Rule-07: For Binary Relationship With Weak Entity Set-

 

Weak entity set always appears in association with identifying relationship with total participation constraint.

 

 

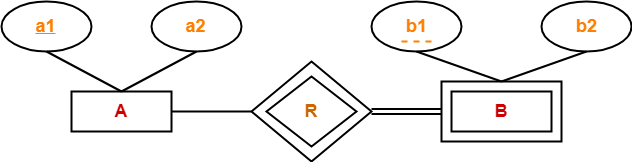
Here, two tables will be required-

  1. A ( a1 , a2 )
  2. BR ( a1 , b1 , b2 )

 

Next Article- Practice Problems On Converting ER Diagrams to Tables

 

Get more notes and other study material of Database Management System (DBMS).

Watch video lectures by visiting our YouTube channel LearnVidFun.

Canonical Cover in DBMS

Database Management System

Canonical Cover in DBMS-

 

Before you go through this article, make sure that you have gone through the previous article on Functional Dependency in DBMS.

 

In DBMS,

  • A canonical cover is a simplified and reduced version of the given set of functional dependencies.
  • Since it is a reduced version, it is also called as Irreducible set.

 

Characteristics-

 

  • Canonical cover is free from all the extraneous functional dependencies.
  • The closure of canonical cover is same as that of the given set of functional dependencies.
  • Canonical cover is not unique and may be more than one for a given set of functional dependencies.

 

Need-

 

  • Working with the set containing extraneous functional dependencies increases the computation time.
  • Therefore, the given set is reduced by eliminating the useless functional dependencies.
  • This reduces the computation time and working with the irreducible set becomes easier.

 

Steps To Find Canonical Cover-

 

Step-01:

 

Write the given set of functional dependencies in such a way that each functional dependency contains exactly one attribute on its right side.

 

Example-

 

The functional dependency X → YZ will be written as-

X → Y

X → Z

 

Step-02:

 

  • Consider each functional dependency one by one from the set obtained in Step-01.
  • Determine whether it is essential or non-essential.

 

To determine whether a functional dependency is essential or not, compute the closure of its left side-

  • Once by considering that the particular functional dependency is present in the set
  • Once by considering that the particular functional dependency is not present in the set

 

Then following two cases are possible-

 

Case-01: Results Come Out to be Same-

 

If results come out to be same,

  • It means that the presence or absence of that functional dependency does not create any difference.
  • Thus, it is non-essential.
  • Eliminate that functional dependency from the set.

 

NOTE-

 

  • Eliminate the non-essential functional dependency from the set as soon as it is discovered.
  • Do not consider it while checking the essentiality of other functional dependencies.

 

Case-01: Results Come Out to be Different-

 

If results come out to be different,

  • It means that the presence or absence of that functional dependency creates a difference.
  • Thus, it is essential.
  • Do not eliminate that functional dependency from the set.
  • Mark that functional dependency as essential.

 

Step-03:

 

  • Consider the newly obtained set of functional dependencies after performing Step-02.
  • Check if there is any functional dependency that contains more than one attribute on its left side.

 

Then following two cases are possible-

 

Case-01: No-

 

  • There exists no functional dependency containing more than one attribute on its left side.
  • In this case, the set obtained in Step-02 is the canonical cover.

 

Case-01: Yes-

 

  • There exists at least one functional dependency containing more than one attribute on its left side.
  • In this case, consider all such functional dependencies one by one.
  • Check if their left side can be reduced.

 

Use the following steps to perform a check-

  • Consider a functional dependency.
  • Compute the closure of all the possible subsets of the left side of that functional dependency.
  • If any of the subsets produce the same closure result as produced by the entire left side, then replace the left side with that subset.

After this step is complete, the set obtained is the canonical cover.

 

PRACTICE PROBLEM BASED ON FINDING CANONICAL COVER-

 

Problem-

 

The following functional dependencies hold true for the relational scheme R ( W , X , Y , Z ) –

X → W

WZ → XY

Y → WXZ

Write the irreducible equivalent for this set of functional dependencies.

 

Solution-

 

Step-01:

 

Write all the functional dependencies such that each contains exactly one attribute on its right side-

X → W

WZ → X

WZ → Y

Y → W

Y → X

Y → Z

 

Step-02:

 

Check the essentiality of each functional dependency one by one.

 

For X → W:

 

  • Considering X → W, (X)+ = { X , W }
  • Ignoring X → W, (X)+ = { X }

 

Now,

  • Clearly, the two results are different.
  • Thus, we conclude that X → W is essential and can not be eliminated.

 

For WZ → X:

 

  • Considering WZ → X, (WZ)+ = { W , X , Y , Z }
  • Ignoring WZ → X, (WZ)+ = { W , X , Y , Z }

 

Now,

  • Clearly, the two results are same.
  • Thus, we conclude that WZ → X is non-essential and can be eliminated.

 

Eliminating WZ → X, our set of functional dependencies reduces to-

X → W

WZ → Y

Y → W

Y → X

Y → Z

Now, we will consider this reduced set in further checks.

 

For WZ → Y:

 

  • Considering WZ → Y, (WZ)+ = { W , X , Y , Z }
  • Ignoring WZ → Y, (WZ)+ = { W , Z }

 

Now,

  • Clearly, the two results are different.
  • Thus, we conclude that WZ → Y is essential and can not be eliminated.

 

For Y → W:

 

  • Considering Y → W, (Y)+ = { W , X , Y , Z }
  • Ignoring Y → W, (Y)+ = { W , X , Y , Z }

 

Now,

  • Clearly, the two results are same.
  • Thus, we conclude that Y → W is non-essential and can be eliminated.

 

Eliminating Y → W, our set of functional dependencies reduces to-

X → W

WZ → Y

Y → X

Y → Z

 

For Y → X:

 

  • Considering Y → X, (Y)+ = { W , X , Y , Z }
  • Ignoring Y → X, (Y)+ = { Y , Z }

 

Now,

  • Clearly, the two results are different.
  • Thus, we conclude that Y → X is essential and can not be eliminated.

 

For Y → Z:

 

  • Considering Y → Z, (Y)+ = { W , X , Y , Z }
  • Ignoring Y → Z, (Y)+ = { W , X , Y }

 

Now,

  • Clearly, the two results are different.
  • Thus, we conclude that Y → Z is essential and can not be eliminated.

 

From here, our essential functional dependencies are-

X → W

WZ → Y

Y → X

Y → Z

 

Step-03:

 

  • Consider the functional dependencies having more than one attribute on their left side.
  • Check if their left side can be reduced.

 

In our set,

  • Only WZ → Y contains more than one attribute on its left side.
  • Considering WZ → Y, (WZ)+ = { W , X , Y , Z }

 

Now,

  • Consider all the possible subsets of WZ.
  • Check if the closure result of any subset matches to the closure result of WZ.

(W)+ = { W }

(Z)+ = { Z }

 

Clearly,

  • None of the subsets have the same closure result same as that of the entire left side.
  • Thus, we conclude that we can not write WZ → Y as W → Y or Z → Y.
  • Thus, set of functional dependencies obtained in step-02 is the canonical cover.

 

Finally, the canonical cover is-

X → W

WZ → Y

Y → X

Y → Z

Canonical Cover

 

Next Article- Decomposition of a Relation

 

Get more notes and other study material of Database Management System (DBMS).

Watch video lectures by visiting our YouTube channel LearnVidFun.

Types of Keys in DBMS | Definitions | Examples

Database Management System

Keys in DBMS-

 

A key is a set of attributes that can identify each tuple uniquely in the given relation.

 

Also read- Attributes in DBMS

 

Different Types Of Keys in DBMS-

 

There are following 10 important keys in DBMS-

 

 

  1. Super key
  2. Candidate key
  3. Primary key
  4. Alternate key
  5. Foreign key
  6. Partial key
  7. Composite key
  8. Unique key
  9. Surrogate key
  10. Secondary key

 

NOTE-

 

Before proceeding further, Kindly note-

  • The terms ‘relation’ and ‘table’ are used interchangeably.
  • The terms ‘tuple’ and ‘record’ are used interchangeably.

So, don’t get confused!

 

1. Super Key-

 

  • A super key is a set of attributes that can identify each tuple uniquely in the given relation.
  • A super key is not restricted to have any specific number of attributes.
  • Thus, a super key may consist of any number of attributes.

 

Example-

 

Consider the following Student schema-

Student ( roll , name , sex , age , address , class , section )

 

Given below are the examples of super keys since each set can uniquely identify each student in the Student table-

  • ( roll , name , sex , age , address , class , section )
  • ( class , section , roll )
  • (class , section , roll , sex )
  • ( name , address )

 

NOTE-

 

All the attributes in a super key are definitely sufficient to identify each tuple uniquely in the given relation but all of them may not be necessary.

 

2. Candidate Key-

 

A minimal super key is called as a candidate key.

OR

A set of minimal attribute(s) that can identify each tuple uniquely in the given relation is called as a candidate key.

 

Example-

 

Consider the following Student schema-

Student ( roll , name , sex , age , address , class , section )

 

Given below are the examples of candidate keys since each set consists of minimal attributes required to identify each student uniquely in the Student table-

  • ( class , section , roll )
  • ( name , address )

 

NOTES-

 

  • All the attributes in a candidate key are sufficient as well as necessary to identify each tuple uniquely.
  • Removing any attribute from the candidate key fails in identifying each tuple uniquely.
  • The value of candidate key must always be unique.
  • The value of candidate key can never be NULL.
  • It is possible to have multiple candidate keys in a relation.
  • Those attributes which appears in some candidate key are called as prime attributes.

 

3. Primary Key-

 

A primary key is a candidate key that the database designer selects while designing the database.

OR

Candidate key that the database designer implements is called as a primary key.

 

NOTES-

 

  • The value of primary key can never be NULL.
  • The value of primary key must always be unique.
  • The values of primary key can never be changed i.e. no updation is possible.
  • The value of primary key must be assigned when inserting a record.
  • A relation is allowed  to have only one primary key.

 

Remember-

 

 

4. Alternate Key-

 

Candidate keys that are left unimplemented or unused after implementing the primary key are called as alternate keys.

OR

Unimplemented candidate keys are called as alternate keys.

 

5. Foreign Key-

 

  • An attribute ‘X’ is called as a foreign key to some other attribute ‘Y’ when its values are dependent on the values of attribute ‘Y’.
  • The attribute ‘X’ can assume only those values which are assumed by the attribute ‘Y’.
  • Here, the relation in which attribute ‘Y’ is present is called as the referenced relation.
  • The relation in which attribute ‘X’ is present is called as the referencing relation.
  • The attribute ‘Y’ might be present in the same table or in some other table.

 

Example-

 

Consider the following two schemas-

 

Here, t_dept can take only those values which are present in dept_no in Department table since only those departments actually exist.

 

NOTES-

 

  • Foreign key references the primary key of the table.
  • Foreign key can take only those values which are present in the primary key of the referenced relation.
  • Foreign key may have a name other than that of a primary key.
  • Foreign key can take the NULL value.
  • There is no restriction on a foreign key to be unique.
  • In fact, foreign key is not unique most of the time.
  • Referenced relation may also be called as the master table or primary table.
  • Referencing relation may also be called as the foreign table.

 

6. Partial Key-

 

  • Partial key is a key using which all the records of the table can not be identified uniquely.
  • However, a bunch of related tuples can be selected from the table using the partial key.

 

Example-

 

Consider the following schema-

Department ( Emp_no , Dependent_name , Relation )

 

Emp_no Dependent_name Relation
E1 Suman Mother
E1 Ajay Father
E2 Vijay Father
E2 Ankush Son

 

Here, using partial key Emp_no, we can not identify a tuple uniquely but we can select a bunch of tuples from the table.

 

7. Composite Key-

 

A primary key comprising of multiple attributes and not just a single attribute is called as a composite key.

 

8. Unique Key-

 

Unique key is a key with the following properties-

  • It is unique for all the records of the table.
  • Once assigned, its value can not be changed i.e. it is non-updatable.
  • It may have a NULL value.

 

Example-

 

The best example of unique key is Adhaar Card Numbers.

  • The Adhaar Card Number is unique for all the citizens (tuples) of India (table).
  • If it gets lost and another duplicate copy is issued, then the duplicate copy always has the same number as before.
  • Thus, it is non-updatable.
  • Few citizens may not have got their Adhaar cards, so for them its value is NULL.

 

9. Surrogate Key-

 

Surrogate key is a key with the following properties-

  • It is unique for all the records of the table.
  • It is updatable.
  • It can not be NULL i.e. it must have some value.

 

Example-

 

Mobile Number of students in a class where every student owns a mobile phone.

 

10. Secondary Key-

 

Secondary key is required for the indexing purpose for better and faster searching.

 

Next Article- Finding Candidate Keys of Given Relation

 

Get more notes and other study material of Database Management System (DBMS).

Watch video lectures by visiting our YouTube channel LearnVidFun.

Determine Decomposition Is Lossless Or Lossy

Database Management System

Decomposition in DBMS-

 

Before you go through this article, make sure that you have gone through the previous article on Decomposition in DBMS.

 

We have discussed-

  • Decomposition is a process of dividing a single relation into two or more sub relations.
  • Decomposition of a relation can be completed in the following two ways-

 

 

  1. Lossless Join Decomposition
  2. Lossy Join Decomposition

 

In this article, we will learn how to determine whether the decomposition is lossless or lossy.

 

Determining Whether Decomposition Is Lossless Or Lossy-

 

Consider a relation R is decomposed into two sub relations R1 and R2.

Then,

  • If all the following conditions satisfy, then the decomposition is lossless.
  • If any of these conditions fail, then the decomposition is lossy.

 

Condition-01:

 

Union of both the sub relations must contain all the attributes that are present in the original relation R.

Thus,

R1 ∪ R2 = R

 

Condition-02:

 

  • Intersection of both the sub relations must not be null.
  • In other words, there must be some common attribute which is present in both the sub relations.

Thus,

R1 ∩ R2 ≠ ∅

 

Condition-03:

 

Intersection of both the sub relations must be a super key of either R1 or R2 or both.

Thus,

R1 ∩ R2 = Super key of R1 or R2

 

PRACTICE PROBLEMS BASED ON DETERMINING WHETHER DECOMPOSITION IS LOSSLESS OR LOSSY-

 

Problem-01:

 

Consider a relation schema R ( A , B , C , D ) with the functional dependencies A → B and C → D. Determine whether the decomposition of R into R1 ( A , B ) and R2 ( C , D ) is lossless or lossy.

 

Solution-

 

To determine whether the decomposition is lossless or lossy,

  • We will check all the conditions one by one.
  • If any of the conditions fail, then the decomposition is lossy otherwise lossless.

 

Condition-01:

 

According to condition-01, union of both the sub relations must contain all the attributes of relation R.

So, we have-

 R1 ( A , B ) ∪ R2 ( C , D )

= R ( A , B , C , D )

Clearly, union of the sub relations contain all the attributes of relation R.

Thus, condition-01 satisfies.

 

Condition-02:

 

According to condition-02, intersection of both the sub relations must not be null.

So, we have-

R1 ( A , B ) ∩ R2 ( C , D )

= Φ

Clearly, intersection of the sub relations is null.

So, condition-02 fails.

Thus, we conclude that the decomposition is lossy.

 

Problem-02:

 

Consider a relation schema R ( A , B , C , D ) with the following functional dependencies-

A → B

B → C

C → D

D → B

Determine whether the decomposition of R into R1 ( A , B ) , R2 ( B , C ) and R3 ( B , D ) is lossless or lossy.

 

Solution-

 

Strategy to Solve

 

When a given relation is decomposed into more than two sub relations, then-

  • Consider any one possible ways in which the relation might have been decomposed into those sub relations.
  • First, divide the given relation into two sub relations.
  • Then, divide the sub relations according to the sub relations given in the question.

As a thumb rule, remember-

Any relation can be decomposed only into two sub relations at a time.

 

Consider the original relation R was decomposed into the given sub relations as shown-

 

 

Decomposition of R(A, B, C, D) into R'(A, B, C) and R3(B, D)-

 

To determine whether the decomposition is lossless or lossy,

  • We will check all the conditions one by one.
  • If any of the conditions fail, then the decomposition is lossy otherwise lossless.

 

Condition-01:

 

According to condition-01, union of both the sub relations must contain all the attributes of relation R.

So, we have-

 R‘ ( A , B , C ) ∪ R3 ( B , D )

= R ( A , B , C , D )

Clearly, union of the sub relations contain all the attributes of relation R.

Thus, condition-01 satisfies.

 

Condition-02:

 

According to condition-02, intersection of both the sub relations must not be null.

So, we have-

 R‘ ( A , B , C ) ∩ R3 ( B , D )

= B

Clearly, intersection of the sub relations is not null.

Thus, condition-02 satisfies.

 

Condition-03:

 

According to condition-03, intersection of both the sub relations must be the super key of one of the two sub relations or both.

So, we have-

 R‘ ( A , B , C ) ∩ R3 ( B , D )

= B

Now, the closure of attribute B is-

B+ = { B , C , D }

Now, we see-

  • Attribute ‘B’ can not determine attribute ‘A’ of sub relation R’.
  • Thus, it is not a super key of the sub relation R’.
  • Attribute ‘B’ can determine all the attributes of sub relation R3.
  • Thus, it is a super key of the sub relation R3.

 

Clearly, intersection of the sub relations is a super key of one of the sub relations.

So, condition-03 satisfies.

Thus, we conclude that the decomposition is lossless.

 

Decomposition of R'(A, B, C) into R1(A, B) and R2(B, C)-

 

To determine whether the decomposition is lossless or lossy,

  • We will check all the conditions one by one.
  • If any of the conditions fail, then the decomposition is lossy otherwise lossless.

 

Condition-01:

 

According to condition-01, union of both the sub relations must contain all the attributes of relation R’.

So, we have-

 R1 ( A , B ) ∪ R2 ( B , C )

= R’ ( A , B , C )

Clearly, union of the sub relations contain all the attributes of relation R’.

Thus, condition-01 satisfies.

 

Condition-02:

 

According to condition-02, intersection of both the sub relations must not be null.

So, we have-

 R1 ( A , B ) ∩ R2 ( B , C )

= B

Clearly, intersection of the sub relations is not null.

Thus, condition-02 satisfies.

 

Condition-03:

 

According to condition-03, intersection of both the sub relations must be the super key of one of the two sub relations or both.

So, we have-

 R1 ( A , B ) ∩ R2 ( B , C )

= B

Now, the closure of attribute B is-

B+ = { B , C , D }

Now, we see-

  • Attribute ‘B’ can not determine attribute ‘A’ of sub relation R1.
  • Thus, it is not a super key of the sub relation R1.
  • Attribute ‘B’ can determine all the attributes of sub relation R2.
  • Thus, it is a super key of the sub relation R2.

 

Clearly, intersection of the sub relations is a super key of one of the sub relations.

So, condition-03 satisfies.

Thus, we conclude that the decomposition is lossless.

 

Conclusion-

Overall decomposition of relation R into sub relations R1, R2 and R3 is lossless.

 

Next Article- Introduction to Normal Forms

 

Get more notes and other study material of Database Management System (DBMS).

Watch video lectures by visiting our YouTube channel LearnVidFun.

Closure in DBMS | Steps to Find Closure

Database Management System

Closure of an Attribute Set-

 

  • The set of all those attributes which can be functionally determined from an attribute set is called as a closure of that attribute set.
  • Closure of attribute set {X} is denoted as {X}+.

 

Steps to Find Closure of an Attribute Set-

 

Following steps are followed to find the closure of an attribute set-

 

Step-01:

 

Add the attributes contained in the attribute set for which closure is being calculated to the result set.

 

Step-02:

 

Recursively add the attributes to the result set which can be functionally determined from the attributes already contained in the result set.

 

Example-

 

Consider a relation R ( A , B , C , D , E , F , G ) with the functional dependencies-

A → BC

BC → DE

D → F

CF → G

 

Now, let us find the closure of some attributes and attribute sets-

 

Closure of attribute A-

 

A+   = { A }

= { A , B , C }                          ( Using A → BC )

= { A , B , C , D , E }               ( Using BC → DE )

= { A , B , C , D , E , F }          ( Using D → F )

= { A , B , C , D , E , F , G }    ( Using CF → G )

Thus,

A+ = { A , B , C , D , E , F , G }

 

Closure of attribute D-

 

D+   = { D }

= { D , F }   ( Using D → F )

We can not determine any other attribute using attributes D and F contained in the result set.

Thus,

D+ = { D , F }

 

Closure of attribute set {B, C}-

 

{ B , C }+= { B , C }

= { B , C , D , E }               ( Using BC → DE )

= { B , C , D , E , F }          ( Using D → F )

= { B , C , D , E , F , G }    ( Using CF → G )

Thus,

{ B , C }+ = { B , C , D , E , F , G }

 

Finding the Keys Using Closure-

 

Super Key-

 

  • If the closure result of an attribute set contains all the attributes of the relation, then that attribute set is called as a super key of that relation.
  • Thus, we can say-

“The closure of a super key is the entire relation schema.”

 

Example-

 

In the above example,

  • The closure of attribute A is the entire relation schema.
  • Thus, attribute A is a super key for that relation.

 

Candidate Key-

 

  • If there exists no subset of an attribute set whose closure contains all the attributes of the relation, then that attribute set is called as a candidate key of that relation.

 

Example-

 

In the above example,

  • No subset of attribute A contains all the attributes of the relation.
  • Thus, attribute A is also a candidate key for that relation.

 

Also Read- How To Find Candidate Keys?

 

PRACTICE PROBLEM BASED ON FINDING CLOSURE OF AN ATTRIBUTE SET-

 

Problem-

 

Consider the given functional dependencies-

AB → CD

AF → D

DE → F

C → G

F → E

G → A

 

Which of the following options is false?

(A) { CF }+ = { A , C , D , E , F , G }

(B) { BG }+ = { A , B , C , D , G }

(C) { AF }+ = { A , C , D , E , F , G }

(D) { AB }+ = { A , C , D , F ,G }

 

Solution-

 

Let us check each option one by one-

 

Option-(A):

 

{ CF }+  = { C , F }

      = { C , F , G }                     ( Using C → G )

      = { C , E , F , G }               ( Using F → E )

      = { A , C , E , E , F }          ( Using G → A )

      = { A , C , D , E , F , G }    ( Using AF → D )

 

Since, our obtained result set is same as the given result set, so, it means it is correctly given.

 

Option-(B):

 

{ BG }+  = { B , G }

      = { A , B , G }                   ( Using G → A )

      = { A , B , C , D , G }        ( Using AB → CD )

 

Since, our obtained result set is same as the given result set, so, it means it is correctly given.

 

Option-(C):

 

{ AF }+  = { A , F }

      = { A , D , F }               ( Using AF → D )

      = { A , D , E , F }          ( Using F → E )

 

Since, our obtained result set is different from the given result set, so,it means it is not correctly given.

 

Option-(D):

 

{ AB }+  = { A , B }

      = { A , B , C , D }            ( Using AB → CD )

      = { A , B , C , D , G }      ( Using C → G )

 

Since, our obtained result set is different from the given result set, so,it means it is not correctly given.

Thus,

Option (C) and Option (D) are correct.

 

Next Article- 10 Different Kinds of Keys in DBMS

 

Get more notes and other study material of Database Management System (DBMS).

Watch video lectures by visiting our YouTube channel LearnVidFun.