Direct Mapping-
Before you go through this article, make sure that you have gone through the previous article on Direct Mapping.
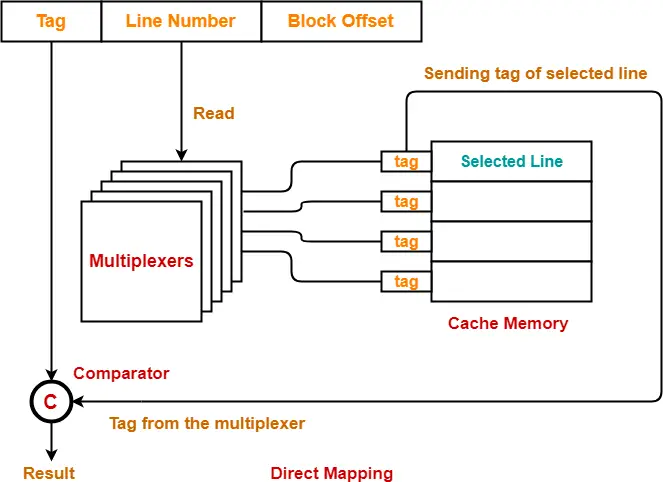
In direct mapping,
- A particular block of main memory can be mapped to one particular cache line only.
- Block ‘j’ of main memory will map to line number (j mod number of cache lines) of the cache.
- There is no need of any replacement algorithm.
In this article, we will discuss practice problems based on direct mapping.
Also Read- Cache Mapping Techniques
PRACTICE PROBLEMS BASED ON DIRECT MAPPING-
Problem-01:
Consider a direct mapped cache of size 16 KB with block size 256 bytes. The size of main memory is 128 KB. Find-
- Number of bits in tag
- Tag directory size
Solution-
Given-
- Cache memory size = 16 KB
- Block size = Frame size = Line size = 256 bytes
- Main memory size = 128 KB
We consider that the memory is byte addressable.
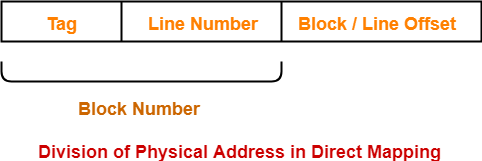
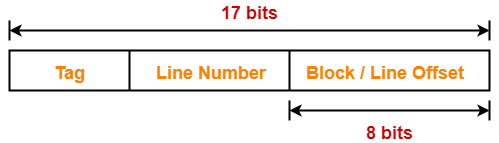
Number of Bits in Physical Address-
We have,
Size of main memory
= 128 KB
= 217 bytes
Thus, Number of bits in physical address = 17 bits

Number of Bits in Block Offset-
We have,
Block size
= 256 bytes
= 28 bytes
Thus, Number of bits in block offset = 8 bits
Number of Bits in Line Number-
Total number of lines in cache
= Cache size / Line size
= 16 KB / 256 bytes
= 214 bytes / 28 bytes
= 26 lines
Thus, Number of bits in line number = 6 bits
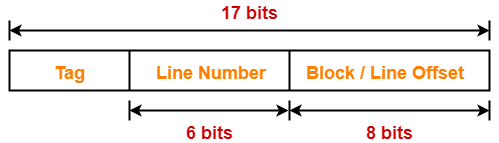
Number of Bits in Tag-
Number of bits in tag
= Number of bits in physical address – (Number of bits in line number + Number of bits in block offset)
= 17 bits – (6 bits + 8 bits)
= 17 bits – 14 bits
= 3 bits
Thus, Number of bits in tag = 3 bits
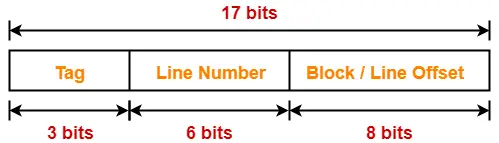
Tag Directory Size-
Tag directory size
= Number of tags x Tag size
= Number of lines in cache x Number of bits in tag
= 26 x 3 bits
= 192 bits
= 24 bytes
Thus, size of tag directory = 24 bytes
Problem-02:
Consider a direct mapped cache of size 512 KB with block size 1 KB. There are 7 bits in the tag. Find-
- Size of main memory
- Tag directory size
Solution-
Given-
- Cache memory size = 512 KB
- Block size = Frame size = Line size = 1 KB
- Number of bits in tag = 7 bits
We consider that the memory is byte addressable.
Number of Bits in Block Offset-
We have,
Block size
= 1 KB
= 210 bytes
Thus, Number of bits in block offset = 10 bits

Number of Bits in Line Number-
Total number of lines in cache
= Cache size / Line size
= 512 KB / 1 KB
= 29 lines
Thus, Number of bits in line number = 9 bits

Number of Bits in Physical Address-
Number of bits in physical address
= Number of bits in tag + Number of bits in line number + Number of bits in block offset
= 7 bits + 9 bits + 10 bits
= 26 bits
Thus, Number of bits in physical address = 26 bits
Size of Main Memory-
We have,
Number of bits in physical address = 26 bits
Thus, Size of main memory
= 226 bytes
= 64 MB
Tag Directory Size-
Tag directory size
= Number of tags x Tag size
= Number of lines in cache x Number of bits in tag
= 29 x 7 bits
= 3584 bits
= 448 bytes
Thus, size of tag directory = 448 bytes
Problem-03:
Consider a direct mapped cache with block size 4 KB. The size of main memory is 16 GB and there are 10 bits in the tag. Find-
- Size of cache memory
- Tag directory size
Solution-
Given-
- Block size = Frame size = Line size = 4 KB
- Size of main memory = 16 GB
- Number of bits in tag = 10 bits
We consider that the memory is byte addressable.
Number of Bits in Physical Address-
We have,
Size of main memory
= 16 GB
= 234 bytes
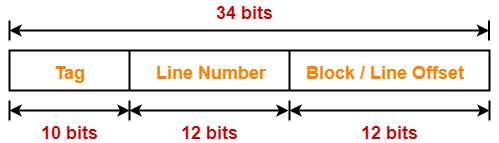
Thus, Number of bits in physical address = 34 bits
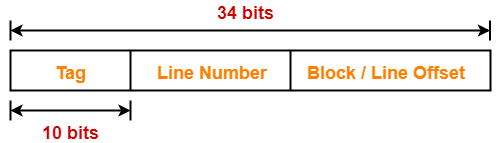
Number of Bits in Block Offset-
We have,
Block size
= 4 KB
= 212 bytes
Thus, Number of bits in block offset = 12 bits
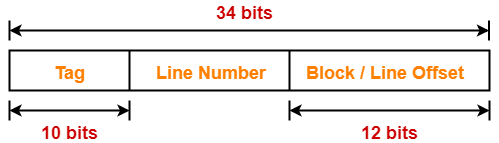
Number of Bits in Line Number-
Number of bits in line number
= Number of bits in physical address – (Number of bits in tag + Number of bits in block offset)
= 34 bits – (10 bits + 12 bits)
= 34 bits – 22 bits
= 12 bits
Thus, Number of bits in line number = 12 bits
Number of Lines in Cache-
We have-
Number of bits in line number = 12 bits
Thus, Total number of lines in cache = 212 lines
Size of Cache Memory-
Size of cache memory
= Total number of lines in cache x Line size
= 212 x 4 KB
= 214 KB
= 16 MB
Thus, Size of cache memory = 16 MB
Tag Directory Size-
Tag directory size
= Number of tags x Tag size
= Number of lines in cache x Number of bits in tag
= 212 x 10 bits
= 40960 bits
= 5120 bytes
Thus, size of tag directory = 5120 bytes
Also Read- Practice Problems On Set Associative Mapping
Problem-04:
Consider a direct mapped cache of size 32 KB with block size 32 bytes. The CPU generates 32 bit addresses. The number of bits needed for cache indexing and the number of tag bits are respectively-
- 10, 17
- 10, 22
- 15, 17
- 5, 17
Solution-
Given-
- Cache memory size = 32 KB
- Block size = Frame size = Line size = 32 bytes
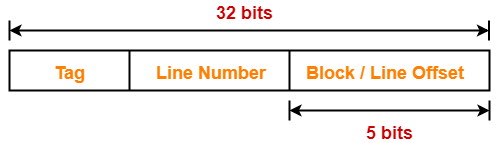
- Number of bits in physical address = 32 bits
Number of Bits in Block Offset-
We have,
Block size
= 32 bytes
= 25 bytes
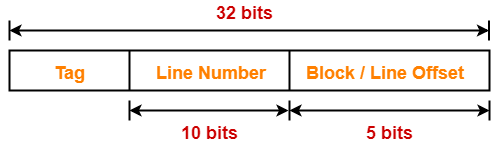
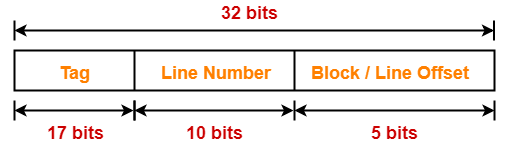
Thus, Number of bits in block offset = 5 bits
Number of Bits in Line Number-
Total number of lines in cache
= Cache size / Line size
= 32 KB / 32 bytes
= 210 lines
Thus, Number of bits in line number = 10 bits
Number of Bits Required For Cache Indexing-
Number of bits required for cache indexing
= Number of bits in line number
= 10 bits
Number Of Bits in Tag-
Number of bits in tag
= Number of bits in physical address – (Number of bits in line number + Number of bits in block offset)
= 32 bits – (10 bits + 5 bits)
= 32 bits – 15 bits
= 17 bits
Thus, Number of bits in tag = 17 bits
Thus, Option (A) is correct.
Problem-05:
Consider a machine with a byte addressable main memory of 232 bytes divided into blocks of size 32 bytes. Assume that a direct mapped cache having 512 cache lines is used with this machine. The size of the tag field in bits is ______.
Solution-
Given-
- Main memory size = 232 bytes
- Block size = Frame size = Line size = 32 bytes
- Number of lines in cache = 512 lines
Number of Bits in Physical Address-
We have,
Size of main memory
= 232 bytes
Thus, Number of bits in physical address = 32 bits

Number of Bits in Block Offset-
We have,
Block size
= 32 bytes
= 25 bytes
Thus, Number of bits in block offset = 5 bits
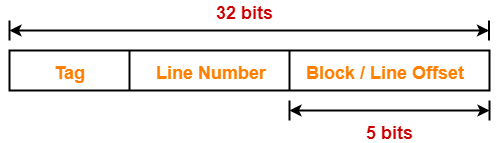
Number of Bits in Line Number-
Total number of lines in cache
= 512 lines
= 29 lines
Thus, Number of bits in line number = 9 bits
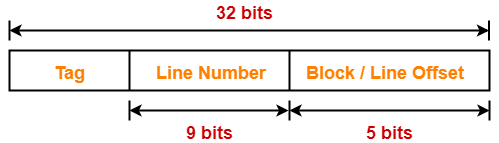
Number Of Bits in Tag-
Number of bits in tag
= Number of bits in physical address – (Number of bits in line number + Number of bits in block offset)
= 32 bits – (9 bits + 5 bits)
= 32 bits – 14 bits
= 18 bits
Thus, Number of bits in tag = 18 bits
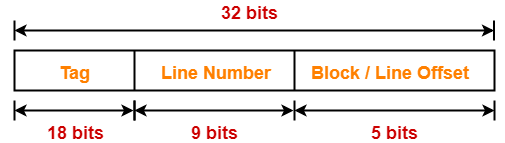
Problem-06:
An 8 KB direct-mapped write back cache is organized as multiple blocks, each of size 32 bytes. The processor generates 32 bit addresses. The cache controller maintains the tag information for each cache block comprising of the following-
- 1 valid bit
- 1 modified bit
- As many bits as the minimum needed to identify the memory block mapped in the cache
What is the total size of memory needed at the cache controller to store meta data (tags) for the cache?
- 4864 bits
- 6144 bits
- 6656 bits
- 5376 bits
Solution-
Given-
- Cache memory size = 8 KB
- Block size = Frame size = Line size = 32 bytes
- Number of bits in physical address = 32 bits
Number of Bits in Block Offset-
We have,
Block size
= 32 bytes
= 25 bytes
Thus, Number of bits in block offset = 5 bits
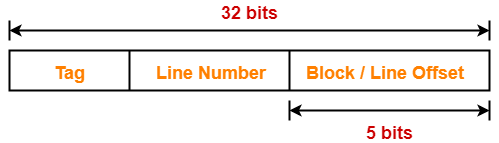
Number of Bits in Line Number-
Total number of lines in cache
= Cache memory size / Line size
= 8 KB / 32 bytes
= 213 bytes / 25 bytes
= 28 lines
Thus, Number of bits in line number = 8 bits
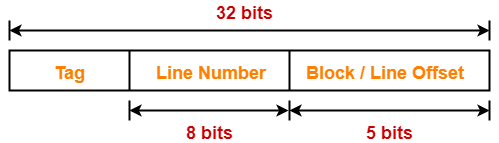
Number Of Bits in Tag-
Number of bits in tag
= Number of bits in physical address – (Number of bits in line number + Number of bits in block offset)
= 32 bits – (8 bits + 5 bits)
= 32 bits – 13 bits
= 19 bits
Thus, Number of bits in tag = 19 bits
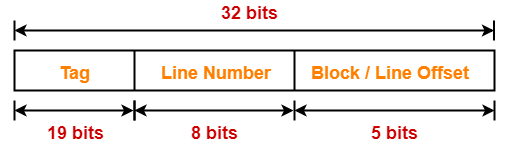
Memory Size Needed At Cache Controller-
Size of memory needed at cache controller
= Number of lines in cache x (1 valid bit + 1 modified bit + 19 bits to identify block)
= 28 x 21 bits
= 5376 bits
To watch video solutions and practice more problems,
Next Article- Practice Problems On Fully Associative Mapping
Get more notes and other study material of Computer Organization and Architecture.
Watch video lectures by visiting our YouTube channel LearnVidFun.