Binary Search Tree-
Before you go through this article, make sure that you have gone through the previous article on BST Operations.
Commonly performed operations on binary search tree are-
- Search Operation
- Insertion Operation
- Deletion Operation
In this article, we will discuss time complexity of BST Operations.
Time Complexity-
- Time complexity of all BST Operations = O(h).
- Here, h = Height of binary search tree
Now, let us discuss the worst case and best case.
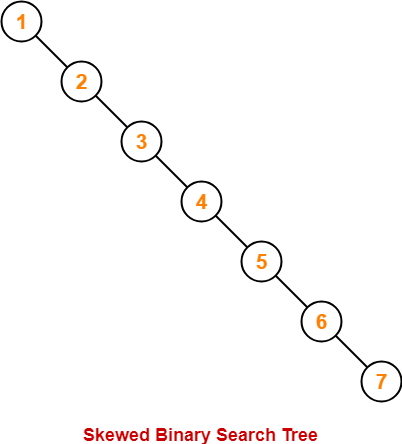
Worst Case-
In worst case,
- The binary search tree is a skewed binary search tree.
- Height of the binary search tree becomes n.
- So, Time complexity of BST Operations = O(n).
In this case, binary search tree is as good as unordered list with no benefits.
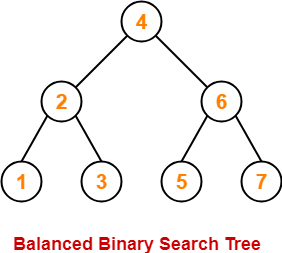
Best Case-
In best case,
- The binary search tree is a balanced binary search tree.
- Height of the binary search tree becomes log(n).
- So, Time complexity of BST Operations = O(logn).
To gain better understanding about Time Complexity of BST Operations,
Download Handwritten Notes Here-
Next Article- Introduction to AVL Trees
Get more notes and other study material of Data Structures.
Watch video lectures by visiting our YouTube channel LearnVidFun.
