Time Complexity of Binary Search Tree

Binary Search Tree-

 

Before you go through this article, make sure that you have gone through the previous article on BST Operations.

 

Commonly performed operations on binary search tree are-

 

 

1. Search Operation
2. Insertion Operation
3. Deletion Operation

 

In this article, we will discuss time complexity of BST Operations.

 

Time Complexity-

 

• Time complexity of all BST Operations = O(h).
• Here, h = Height of binary search tree

 

Now, let us discuss the worst case and best case.

 

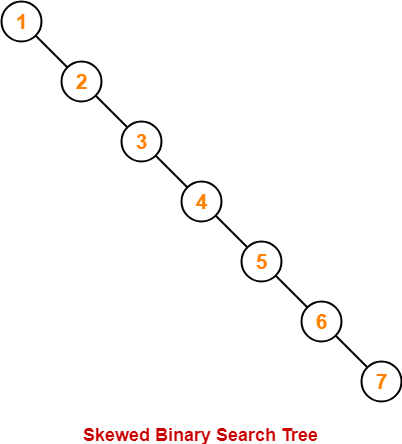
Worst Case-

 

In worst case,

• The binary search tree is a skewed binary search tree.
• Height of the binary search tree becomes n.
• So, Time complexity of BST Operations = O(n).

 

In this case, binary search tree is as good as unordered list with no benefits.

 

 

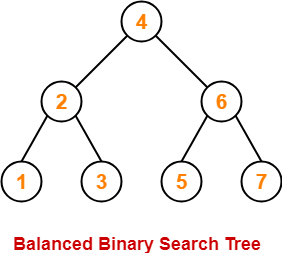
Best Case-

 

In best case,

• The binary search tree is a balanced binary search tree.
• Height of the binary search tree becomes log(n).
• So, Time complexity of BST Operations = O(logn).

 

 

To gain better understanding about Time Complexity of BST Operations,

Watch this Video Lecture

 

Download Handwritten Notes Here-

 

 

Next Article- Introduction to AVL Trees

 

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.