AVL Tree | AVL Tree Example | AVL Tree Rotation

AVL Tree-

 

• AVL trees are special kind of binary search trees.
• In AVL trees, height of left subtree and right subtree of every node differs by at most one.
• AVL trees are also called as self-balancing binary search trees.

 

Also Read- Binary Search Trees

 

Example-

 

Following tree is an example of AVL tree-

 

 

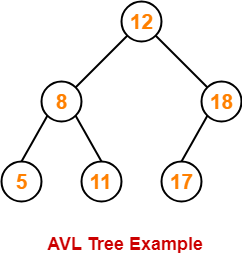
This tree is an AVL tree because-

• It is a binary search tree.
• The difference between height of left subtree and right subtree of every node is at most one.

 

Following tree is not an example of AVL Tree-

 

 

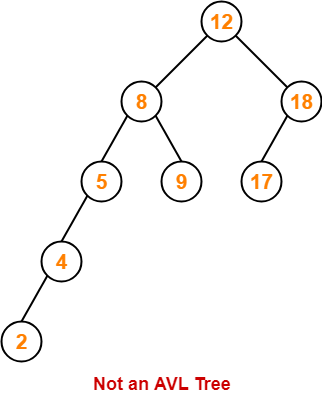
This tree is not an AVL tree because-

• The difference between height of left subtree and right subtree of root node = 4 – 2 = 2.
• This difference is greater than one.

 

Balance Factor-

 

In AVL tree,

• Balance factor is defined for every node.
• Balance factor of a node = Height of its left subtree – Height of its right subtree

 

In AVL tree, Balance factor of every node is either 0 or 1 or -1.

 

AVL Tree Operations-

 

Like BST Operations, commonly performed operations on AVL tree are-

1. Search Operation
2. Insertion Operation
3. Deletion Operation

 

Also Read- Insertion in AVL Tree

 

After performing any operation on AVL tree, the balance factor of each node is checked.

There are following two cases possible-

 

Case-01:

 

• After the operation, the balance factor of each node is either 0 or 1 or -1.
• In this case, the AVL tree is considered to be balanced.
• The operation is concluded.

 

Case-02:

 

• After the operation, the balance factor of at least one node is not 0 or 1 or -1.
• In this case, the AVL tree is considered to be imbalanced.
• Rotations are then performed to balance the tree.

 

AVL Tree Rotations-

 

Rotation is the process of moving the nodes to make tree balanced.

 

Kinds of Rotations-

 

There are 4 kinds of rotations possible in AVL Trees-

 

 

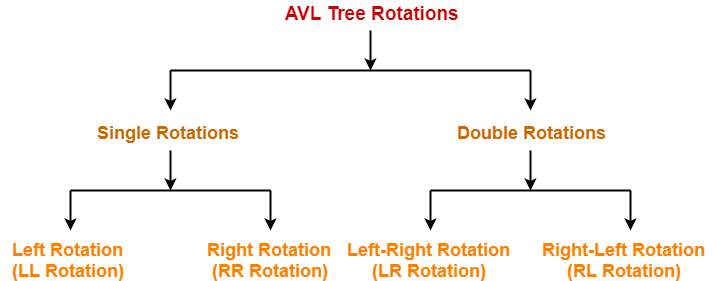
1. Left Rotation (LL Rotation)
2. Right Rotation (RR Rotation)
3. Left-Right Rotation (LR Rotation)
4. Right-Left Rotation (RL Rotation)

 

Cases Of Imbalance And Their Balancing Using Rotation Operations-

 

Case-01:

 

 

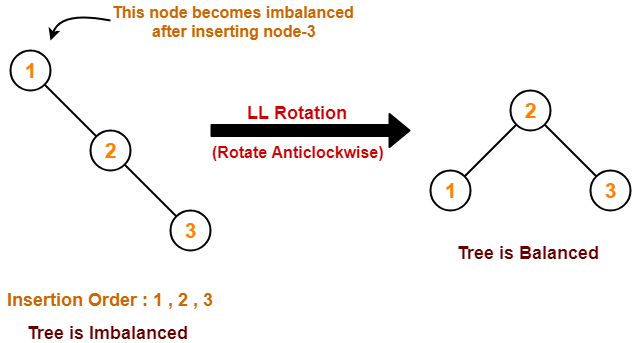
Case-02:

 

 

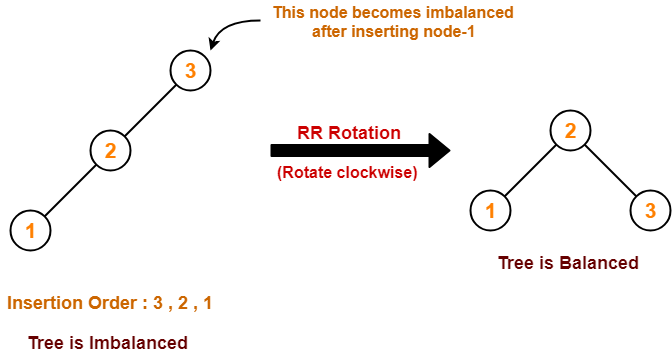
Case-03:

 

 

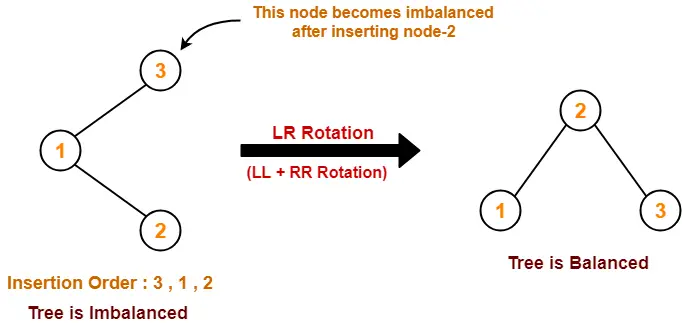
Case-04:

 

 

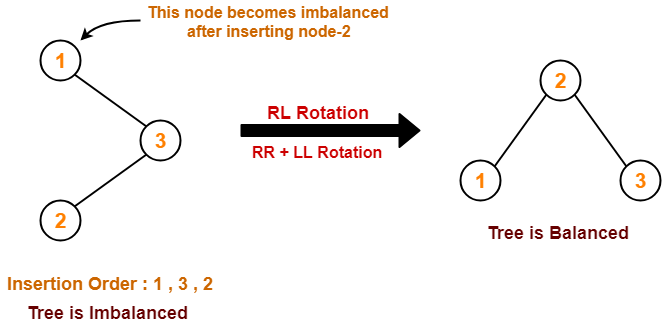
To gain better understanding about AVL Trees and Rotations,

Watch this Video Lecture

 

Download Handwritten Notes Here-

 

 

Next Article- AVL Tree Properties

 

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.