Tag: Binary Search Tree With Example

Time Complexity of Binary Search Tree

Data Structures

Binary Search Tree-

 

Before you go through this article, make sure that you have gone through the previous article on BST Operations.

 

Commonly performed operations on binary search tree are-

 

 

  1. Search Operation
  2. Insertion Operation
  3. Deletion Operation

 

In this article, we will discuss time complexity of BST Operations.

 

Time Complexity-

 

  • Time complexity of all BST Operations = O(h).
  • Here, h = Height of binary search tree

 

Now, let us discuss the worst case and best case.

 

Worst Case-

 

In worst case,

  • The binary search tree is a skewed binary search tree.
  • Height of the binary search tree becomes n.
  • So, Time complexity of BST Operations = O(n).

 

In this case, binary search tree is as good as unordered list with no benefits.

 

 

Best Case-

 

In best case,

  • The binary search tree is a balanced binary search tree.
  • Height of the binary search tree becomes log(n).
  • So, Time complexity of BST Operations = O(logn).

 

 

To gain better understanding about Time Complexity of BST Operations,

Watch this Video Lecture

 

Download Handwritten Notes Here-

 

 

Next Article- Introduction to AVL Trees

 

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Binary Search Tree | Example | Construction

Data Structures

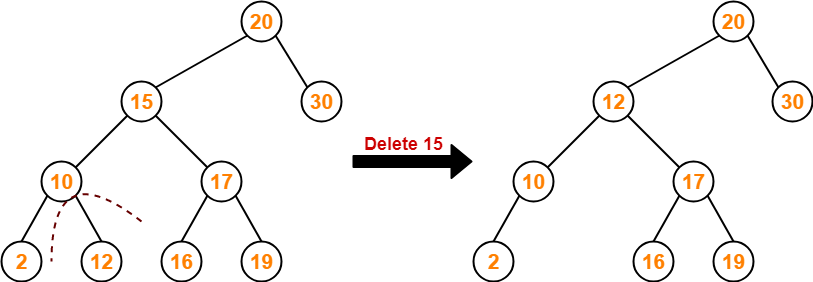
Binary Tree-

 

Before you go through this article, make sure that you gone through the previous article on Binary Trees.

 

We have discussed-

  • Binary tree is a special tree data structure.
  • In a binary tree, each node can have at most 2 children.
  • In a binary tree, nodes may be arranged in any random order.

 

In this article, we will discuss about Binary Search Trees.

 

Binary Search Tree-

 

Binary Search Tree is a special kind of binary tree in which nodes are arranged in a specific order.

 

In a binary search tree (BST), each node contains-

  • Only smaller values in its left sub tree
  • Only larger values in its right sub tree

 

Example-

 

 

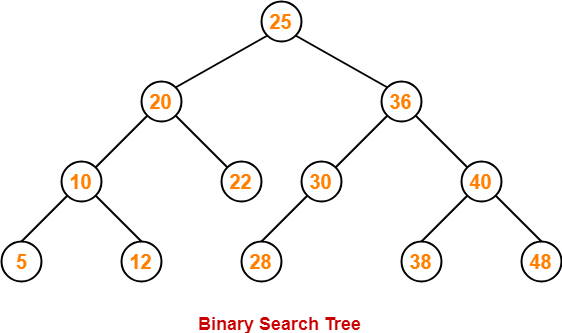
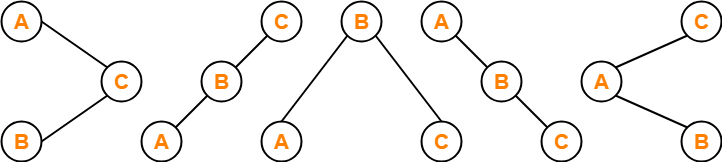
Number of Binary Search Trees-

 

 

Example-

 

Number of distinct binary search trees possible with 3 distinct keys

= 2×3C3 / 3+1

= 6C3 / 4

= 5

 

If three distinct keys are A, B and C, then 5 distinct binary search trees are-

 

 

Binary Search Tree Construction-

 

Let us understand the construction of a binary search tree using the following example-

 

Example-

 

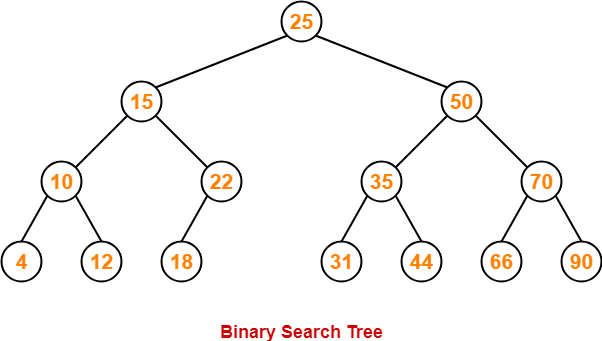
Construct a Binary Search Tree (BST) for the following sequence of numbers-

50, 70, 60, 20, 90, 10, 40, 100

 

When elements are given in a sequence,

  • Always consider the first element as the root node.
  • Consider the given elements and insert them in the BST one by one.

 

The binary search tree will be constructed as explained below-

 

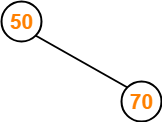
Insert 50-

 

 

Insert 70-

 

  • As 70 > 50, so insert 70 to the right of 50.

 

 

Insert 60-

 

  • As 60 > 50, so insert 60 to the right of 50.
  • As 60 < 70, so insert 60 to the left of 70.

 

 

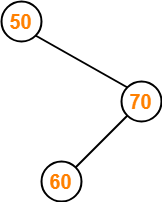
Insert 20-

 

  • As 20 < 50, so insert 20 to the left of 50.

 

 

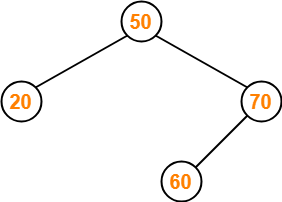
Insert 90-

 

  • As 90 > 50, so insert 90 to the right of 50.
  • As 90 > 70, so insert 90 to the right of 70.

 

 

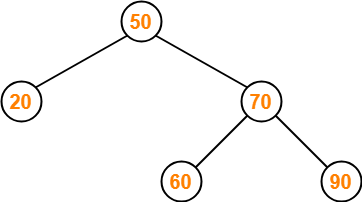
Insert 10-

 

  • As 10 < 50, so insert 10 to the left of 50.
  • As 10 < 20, so insert 10 to the left of 20.

 

 

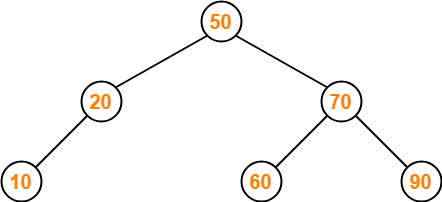
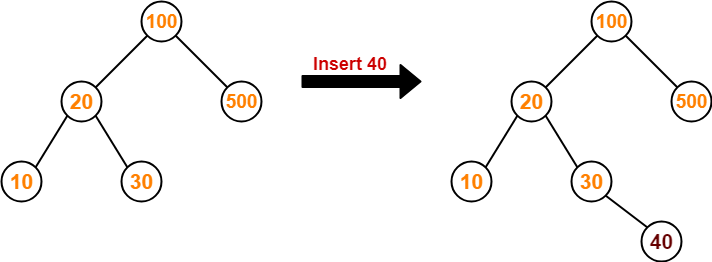
Insert 40-

 

  • As 40 < 50, so insert 40 to the left of 50.
  • As 40 > 20, so insert 40 to the right of 20.

 

 

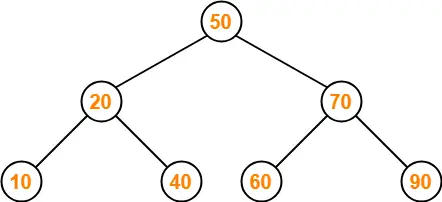
Insert 100-

 

  • As 100 > 50, so insert 100 to the right of 50.
  • As 100 > 70, so insert 100 to the right of 70.
  • As 100 > 90, so insert 100 to the right of 90.

 

 

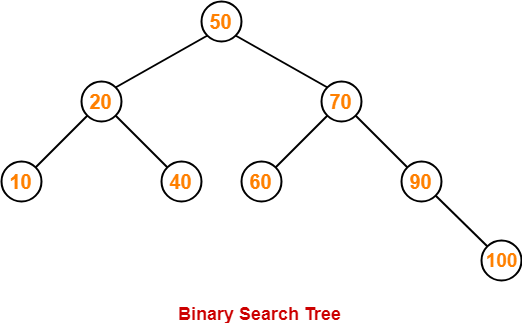
This is the required Binary Search Tree.

 

To gain better understanding about Binary Search Trees,

Watch this Video Lecture

 

PRACTICE PROBLEMS BASED ON BINARY SEARCH TREES-

 

Problem-01:

 

A binary search tree is generated by inserting in order of the following integers-

50, 15, 62, 5, 20, 58, 91, 3, 8, 37, 60, 24

 

The number of nodes in the left subtree and right subtree of the root respectively is _____.

  1. (4, 7)
  2. (7, 4)
  3. (8, 3)
  4. (3, 8)

 

Solution-

 

Using the above discussed steps, we will construct the binary search tree.

The resultant binary search tree will be-

 

 

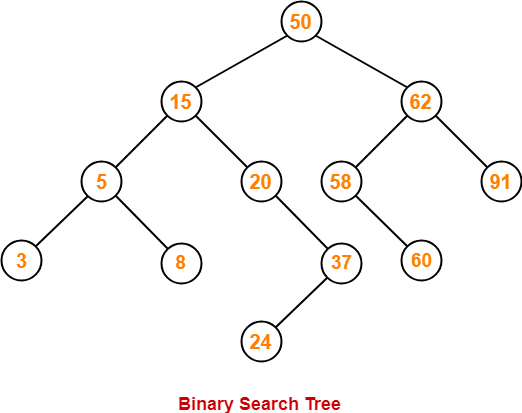
Clearly,

  • Number of nodes in the left subtree of the root = 7
  • Number of nodes in the right subtree of the root = 4

 

Thus, Option (B) is correct.

 

Problem-02:

 

How many distinct binary search trees can be constructed out of 4 distinct keys?

  1. 5
  2. 14
  3. 24
  4. 35

 

Solution-

 

Number of distinct binary search trees possible with 4 distinct keys

= 2nCn / n+1

= 2×4C4 / 4+1

= 8C4 / 5

= 14

 

Thus, Option (B) is correct.

 

Problem-03:

 

The numbers 1, 2, …, n are inserted in a binary search tree in some order. In the resulting tree, the right subtree of the root contains p nodes. The first number to be inserted in the tree must be-

  1. p
  2. p+1
  3. n-p
  4. n-p+1

 

Solution-

 

Let n = 4 and p = 3.

 

Then, given options reduce to-

  1. 3
  2. 4
  3. 1
  4. 2

 

Our binary search tree will be as shown-

 

 

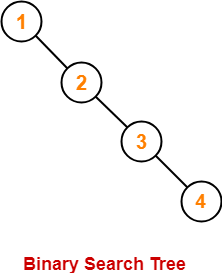
Clearly, first inserted number = 1.

Thus, Option (C) is correct.

 

Problem-04:

 

We are given a set of n distinct elements and an unlabeled binary tree with n nodes. In how many ways can we populate the tree with given set so that it becomes a binary search tree?

  1. 0
  2. 1
  3. n!
  4. C(2n, n) / n+1

 

Solution-

 

Option (B) is correct.

 

To watch video solutions and practice more problems,

Watch this Video Lecture

 

Download Handwritten Notes Here-

 

 

Next Article- Binary Search Tree Traversal

 

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Binary Search Tree Insertion | BST Deletion

Data Structures

Binary Search Tree-

 

Before you go through this article, make sure that you have gone through the previous article on Binary Search Trees.

 

Binary search tree (BST) is a special kind of binary tree where each node contains-

  • Only larger values in its right subtree.
  • Only smaller values in its left subtree.

 

In this article, we will discuss about Binary Search Tree Operations.

 

Binary Search Tree Operations-

 

Commonly performed operations on binary search tree are-

 

 

  1. Search Operation
  2. Insertion Operation
  3. Deletion Operation

 

1. Search Operation-

 

Search Operation is performed to search a particular element in the Binary Search Tree.

 

Rules-

 

For searching a given key in the BST,

  • Compare the key with the value of root node.
  • If the key is present at the root node, then return the root node.
  • If the key is greater than the root node value, then recur for the root node’s right subtree.
  • If the key is smaller than the root node value, then recur for the root node’s left subtree.

 

Example-

 

Consider key = 45 has to be searched in the given BST-

 

 

  • We start our search from the root node 25.
  • As 45 > 25, so we search in 25’s right subtree.
  • As 45 < 50, so we search in 50’s left subtree.
  • As 45 > 35, so we search in 35’s right subtree.
  • As 45 > 44, so we search in 44’s right subtree but 44 has no subtrees.
  • So, we conclude that 45 is not present in the above BST.

 

2. Insertion Operation-

 

Insertion Operation is performed to insert an element in the Binary Search Tree.

 

Rules-

 

The insertion of a new key always takes place as the child of some leaf node.

For finding out the suitable leaf node,

  • Search the key to be inserted from the root node till some leaf node is reached.
  • Once a leaf node is reached, insert the key as child of that leaf node.

 

Example-

 

Consider the following example where key = 40 is inserted in the given BST-

 

 

  • We start searching for value 40 from the root node 100.
  • As 40 < 100, so we search in 100’s left subtree.
  • As 40 > 20, so we search in 20’s right subtree.
  • As 40 > 30, so we add 40 to 30’s right subtree.

 

3. Deletion Operation-

 

Deletion Operation is performed to delete a particular element from the Binary Search Tree.

 

When it comes to deleting a node from the binary search tree, following three cases are possible-

 

Case-01: Deletion Of A Node Having No Child (Leaf Node)-

 

Just remove / disconnect the leaf node that is to deleted from the tree.

 

Example-

 

Consider the following example where node with value = 20 is deleted from the BST-

 

 

Case-02: Deletion Of A Node Having Only One Child-

 

Just make the child of the deleting node, the child of its grandparent.

 

Example-

 

Consider the following example where node with value = 30 is deleted from the BST-

 

 

Case-02: Deletion Of A Node Having Two Children-

 

A node with two children may be deleted from the BST in the following two ways-

 

Method-01:

 

  • Visit to the right subtree of the deleting node.
  • Pluck the least value element called as inorder successor.
  • Replace the deleting element with its inorder successor.

 

Example-

 

Consider the following example where node with value = 15 is deleted from the BST-

 

 

Method-02:

 

  • Visit to the left subtree of the deleting node.
  • Pluck the greatest value element called as inorder predecessor.
  • Replace the deleting element with its inorder predecessor.

 

Example-

 

Consider the following example where node with value = 15 is deleted from the BST-

 

 

To gain better understanding about BST Operations,

Watch this Video Lecture

 

Download Handwritten Notes Here-

 

 

Next Article- Time Complexity of BST Operations

 

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.