Tag: binary trees

Tree Traversal | Binary Tree Traversal

Data Structures

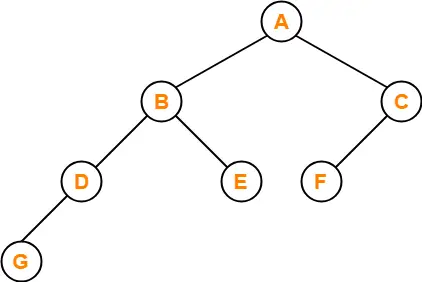
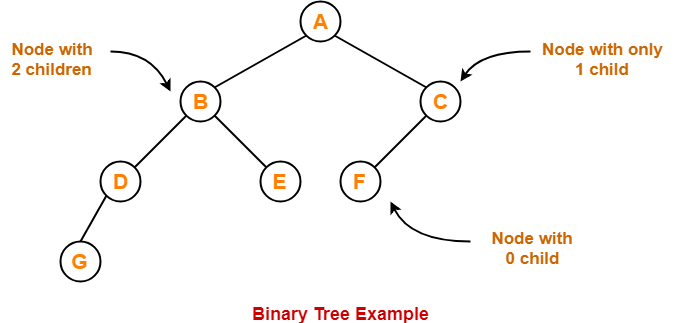
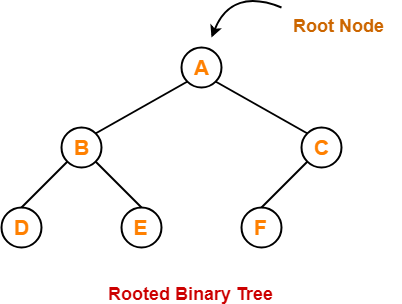
Binary Tree-

 

Before you go through this article, make sure that you gone through the previous article on Binary Trees.

 

We have discussed-

  • Binary tree is a special tree data structure.
  • In a binary tree, each node can have at most 2 children.

 

In this article, we will discuss about Binary Tree Traversal.

 

Tree Traversal-

 

Tree Traversal refers to the process of visiting each node in a tree data structure exactly once.

 

Various tree traversal techniques are-

 

 

Depth First Traversal-

 

Following three traversal techniques fall under Depth First Traversal-

  1. Preorder Traversal
  2. Inorder Traversal
  3. Postorder Traversal

 

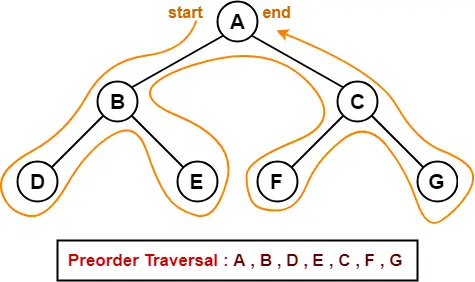
1. Preorder Traversal-

 

Algorithm-

 

  1. Visit the root
  2. Traverse the left sub tree i.e. call Preorder (left sub tree)
  3. Traverse the right sub tree i.e. call Preorder (right sub tree)

 

Root → Left → Right

 

Example-

 

Consider the following example-

 

 

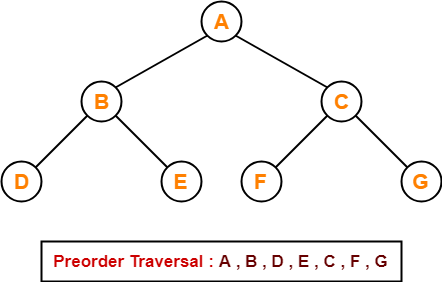
Preorder Traversal Shortcut

 

Traverse the entire tree starting from the root node keeping yourself to the left.

 

 

Applications-

 

  • Preorder traversal is used to get prefix expression of an expression tree.
  • Preorder traversal is used to create a copy of the tree.

 

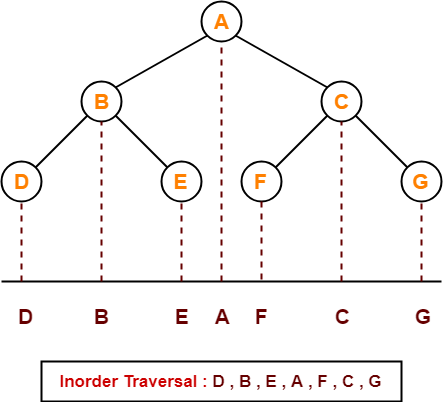
2. Inorder Traversal-

 

Algorithm-

 

  1. Traverse the left sub tree i.e. call Inorder (left sub tree)
  2. Visit the root
  3. Traverse the right sub tree i.e. call Inorder (right sub tree)

 

Left → Root → Right

 

Example-

 

Consider the following example-

 

 

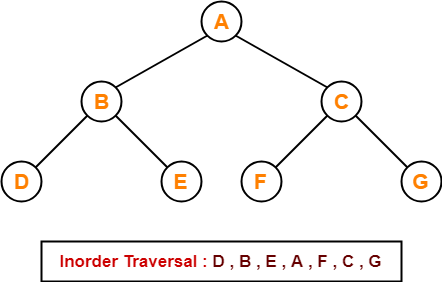
Inorder Traversal Shortcut

 

Keep a plane mirror horizontally at the bottom of the tree and take the projection of all the nodes.

 

 

Application-

 

  • Inorder traversal is used to get infix expression of an expression tree.

 

3. Postorder Traversal-

 

Algorithm-

 

  1. Traverse the left sub tree i.e. call Postorder (left sub tree)
  2. Traverse the right sub tree i.e. call Postorder (right sub tree)
  3. Visit the root

 

Left → Right → Root

 

Example-

 

Consider the following example-

 

 

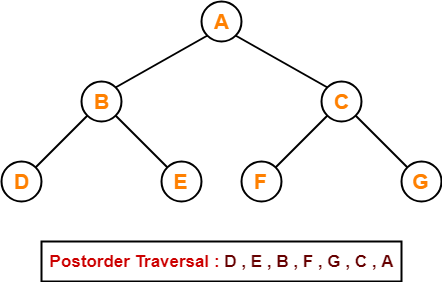
Postorder Traversal Shortcut

 

Pluck all the leftmost leaf nodes one by one.

 

 

Applications-

 

  • Postorder traversal is used to get postfix expression of an expression tree.
  • Postorder traversal is used to delete the tree.
  • This is because it deletes the children first and then it deletes the parent.

 

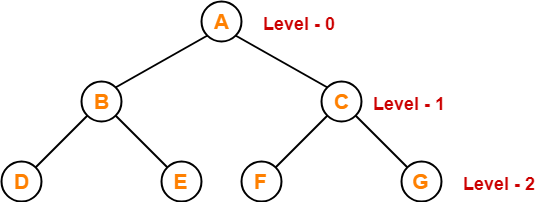
Breadth First Traversal-

 

  • Breadth First Traversal of a tree prints all the nodes of a tree level by level.
  • Breadth First Traversal is also called as Level Order Traversal.

 

Example-

 

 

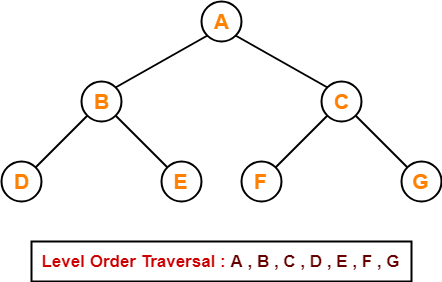
Application-

 

  • Level order traversal is used to print the data in the same order as stored in the array representation of a complete binary tree.

 

To gain better understanding about Tree Traversal,

Watch this Video Lecture

 

Also Read- Binary Tree Properties

 

PRACTICE PROBLEMS BASED ON TREE TRAVERSAL-

 

Problem-01:

 

If the binary tree in figure is traversed in inorder, then the order in which the nodes will be visited is ____?

 

 

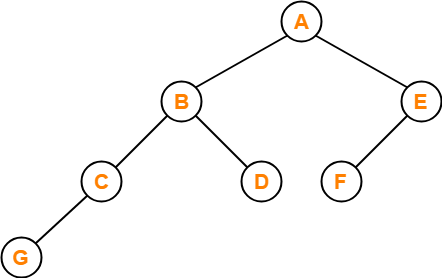
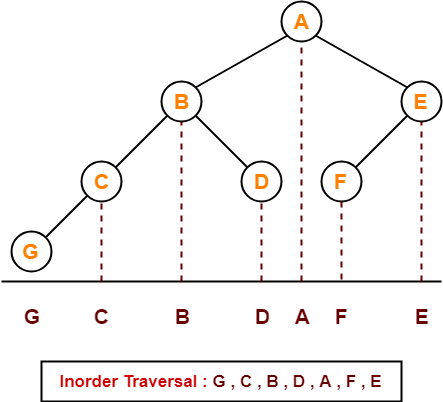
Solution-

 

The inorder traversal will be performed as-

 

 

Problem-02:

 

Which of the following sequences denotes the postorder traversal sequence of the tree shown in figure?

 

 

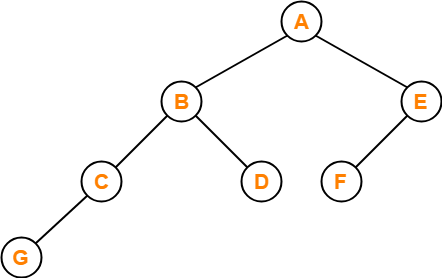
  1. FEGCBDBA
  2. GCBDAFE
  3. GCDBFEA
  4. FDEGCBA

 

Solution-

 

Perform the postorder traversal by plucking all the leftmost leaf nodes one by one.

Then,

Postorder Traversal :  G , C , D , B , F , E , A

 

Thus, Option (C) is correct.

 

Problem-03:

 

Let LASTPOST, LASTIN, LASTPRE denote the last vertex visited in a postorder, inorder and preorder traversal respectively of a complete binary tree. Which of the following is always true?

  1. LASTIN = LASTPOST
  2. LASTIN = LASTPRE
  3. LASTPRE = LASTPOST
  4. None of these

 

Solution-

 

Consider the following complete binary tree-

 

 

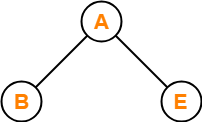
Preorder Traversal  : B , A , E

Inorder Traversal     : B , A , E

Postorder Traversal : B , E , A

 

Clearly, LASTIN = LASTPRE.

Thus, Option (B) is correct.

 

Problem-04:

 

Which of the following binary trees has its inorder and preorder traversals as BCAD and ABCD respectively-

 

 

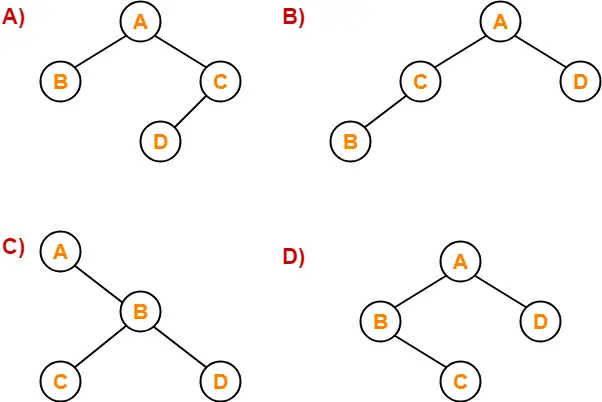
Solution-

 

Option (D) is correct.

 

To watch video solutions and practice more problems,

Watch this Video Lecture

 

Download Handwritten Notes Here-

 

 

Next Article- Binary Search Trees

 

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Binary Tree | Binary Tree Properties

Data Structures

Binary Tree-

 

Before you go through this article, make sure that you gone through the previous article on Binary Trees.

 

We have discussed-

  • Binary tree is a special tree data structure.
  • In a binary tree, each node can have at most 2 children.
  • There are following types of binary trees-

 

 

In this article, we will discuss properties of binary trees.

 

Binary Tree Properties-

 

Important properties of binary trees are-

 

Property-01:

 

Minimum number of nodes in a binary tree of height H

= H + 1

 

Example-

 

To construct a binary tree of height = 4, we need at least 4 + 1 = 5 nodes.

 

 

Property-02:

 

Maximum number of nodes in a binary tree of height H

= 2H+1 – 1

 

Example-

 

Maximum number of nodes in a binary tree of height 3

= 23+1 – 1

= 16 – 1

= 15 nodes

Thus, in a binary tree of height = 3, maximum number of nodes that can be inserted = 15.

 

 

We can not insert more number of nodes in this binary tree.

 

Property-03:

 

Total Number of leaf nodes in a Binary Tree

= Total Number of nodes with 2 children + 1

 

Example-

 

Consider the following binary tree-

 

 

Here,

  • Number of leaf nodes = 3
  • Number of nodes with 2 children = 2

 

Clearly, number of leaf nodes is one greater than number of nodes with 2 children.

This verifies the above relation.

 

NOTE

It is interesting to note that-

Number of leaf nodes in any binary tree depends only on the number of nodes with 2 children.

 

Property-04:

 

Maximum number of nodes at any level ‘L’ in a binary tree

= 2L

 

Example-

 

Maximum number of nodes at level-2 in a binary tree

= 22

= 4

Thus, in a binary tree, maximum number of nodes that can be present at level-2 = 4.

 

 

To gain better understanding about Binary Tree Properties,

Watch this Video Lecture

 

PRACTICE PROBLEMS BASED ON BINARY TREE PROPERTIES-

 

Problem-01:

 

A binary tree T has n leaf nodes. The number of nodes of degree-2 in T is ______?

  1. log2n
  2. n-1
  3. n
  4. 2n

 

Solution-

 

Using property-3, we have-

Number of degree-2 nodes

= Number of leaf nodes – 1

= n – 1

 

Thus, Option (B) is correct.

 

Problem-02:

 

In a binary tree, for every node the difference between the number of nodes in the left and right subtrees is at most 2. If the height of the tree is h > 0, then the minimum number of nodes in the tree is ______?

  1. 2h-1
  2. 2h-1 + 1
  3. 2h – 1
  4. 2h

 

Solution-

 

Let us assume any random value of h. Let h = 3.

Then the given options reduce to-

  1. 4
  2. 5
  3. 7
  4. 8

 

Now, consider the following binary tree with height h = 3-

 

 

  • This binary tree satisfies the question constraints.
  • It is constructed using minimum number of nodes.

 

Thus, Option (B) is correct.

 

Problem-03:

 

In a binary tree, the number of internal nodes of degree-1 is 5 and the number of internal nodes of degree-2 is 10. The number of leaf nodes in the binary tree is ______?

  1. 10
  2. 11
  3. 12
  4. 15

 

Solution-

 

Using property-3, we have-

Number of leaf nodes in a binary tree

= Number of degree-2 nodes + 1

= 10 + 1

= 11

 

Thus, Option (B) is correct.

 

Problem-04:

 

The height of a binary tree is the maximum number of edges in any root to leaf path. The maximum number of nodes in a binary tree of height h is ______?

  1. 2h
  2. 2h-1 – 1
  3. 2h+1 – 1
  4. 2h+1

 

Solution-

 

Using property-2, Option (C) is correct.

 

Problem-05:

 

A binary tree T has 20 leaves. The number of nodes in T having 2 children is ______?

 

Solution-

 

Using property-3, correct answer is 19.

 

To watch video solutions and practice more problems,

Watch this Video Lecture

 

Download Handwritten Notes Here-

 

 

Next Article- Binary Tree Traversal

 

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Binary Tree | Types of Binary Trees

Data Structures

Tree Data Structure-

 

Before you go through this article, make sure that you have gone through the previous article on Tree Data Structure.

 

We have discussed-

  • Tree is a non-linear data structure.
  • In a tree data structure, a node can have any number of child nodes.

 

In this article, we will discuss about Binary Trees.

 

Binary Tree-

 

Binary tree is a special tree data structure in which each node can have at most 2 children.

Thus, in a binary tree,

Each node has either 0 child or 1 child or 2 children.

 

Example-

 

 

Unlabeled Binary Tree-

 

A binary tree is unlabeled if its nodes are not assigned any label.

 

 

 

Example-

 

Consider we want to draw all the binary trees possible with 3 unlabeled nodes.

Using the above formula, we have-

 

Number of binary trees possible with 3 unlabeled nodes

= 2 x 3C3 / (3 + 1)

= 6C3 / 4

= 5

 

Thus,

  • With 3 unlabeled nodes, 5 unlabeled binary trees are possible.
  • These unlabeled binary trees are as follows-

 

 

Labeled Binary Tree-

 

A binary tree is labeled if all its nodes are assigned a label.

 

 

 

Example-

 

Consider we want to draw all the binary trees possible with 3 labeled nodes.

Using the above formula, we have-

 

Number of binary trees possible with 3 labeled nodes

= { 2 x 3C3 / (3 + 1) } x 3!

= { 6C3 / 4 } x 6

= 5 x 6

= 30

 

Thus,

  • With 3 labeled nodes, 30 labeled binary trees are possible.
  • Each unlabeled structure gives rise to 3! = 6 different labeled structures.

 

 

Similarly,

  • Every other unlabeled structure gives rise to 6 different labeled structures.
  • Thus, in total 30 different labeled binary trees are possible.

 

Types of Binary Trees-

 

Binary trees can be of the following types-

 

 

  1. Rooted Binary Tree
  2. Full / Strictly Binary Tree
  3. Complete / Perfect Binary Tree
  4. Almost Complete Binary Tree
  5. Skewed Binary Tree

 

1. Rooted Binary Tree-

 

A rooted binary tree is a binary tree that satisfies the following 2 properties-

  • It has a root node.
  • Each node has at most 2 children.

 

Example-

 

 

2. Full / Strictly Binary Tree-

 

  • A binary tree in which every node has either 0 or 2 children is called as a Full binary tree.
  • Full binary tree is also called as Strictly binary tree.

 

Example-

 

 

Here,

  • First binary tree is not a full binary tree.
  • This is because node C has only 1 child.

 

3. Complete / Perfect Binary Tree-

 

A complete binary tree is a binary tree that satisfies the following 2 properties-

  • Every internal node has exactly 2 children.
  • All the leaf nodes are at the same level.

 

Complete binary tree is also called as Perfect binary tree.

 

Example-

 

 

Here,

  • First binary tree is not a complete binary tree.
  • This is because all the leaf nodes are not at the same level.

 

4. Almost Complete Binary Tree-

 

An almost complete binary tree is a binary tree that satisfies the following 2 properties-

  • All the levels are completely filled except possibly the last level.
  • The last level must be strictly filled from left to right.

 

Example-

 

 

Here,

  • First binary tree is not an almost complete binary tree.
  • This is because the last level is not filled from left to right.

 

5. Skewed Binary Tree-

 

A skewed binary tree is a binary tree that satisfies the following 2 properties-

  • All the nodes except one node has one and only one child.
  • The remaining node has no child.

OR

A skewed binary tree is a binary tree of n nodes such that its depth is (n-1).

 

Example-

 

 

To gain better understanding about Binary Tree and its types-

Watch this Video Lecture

 

Also Read- Binary Tree Traversal

 

Download Handwritten Notes Here-

 

 

Next Article- Binary Tree Properties

 

Get more notes and other study material of Data Structures.

Watch video lectures by visiting our YouTube channel LearnVidFun.