Tree Data Structure-
Tree data structure may be defined as-
| Tree is a non-linear data structure which organizes data in a hierarchical structure and this is a recursive definition.
OR A tree is a connected graph without any circuits. OR If in a graph, there is one and only one path between every pair of vertices, then graph is called as a tree. |
Example-
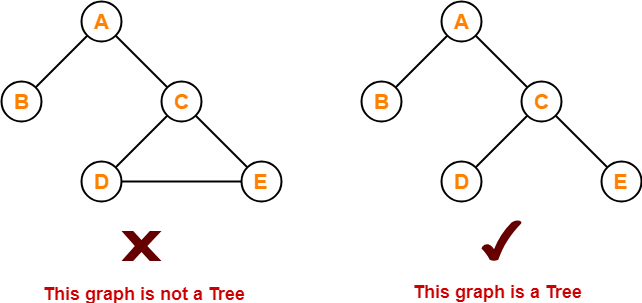
Properties-
The important properties of tree data structure are-
- There is one and only one path between every pair of vertices in a tree.
- A tree with n vertices has exactly (n-1) edges.
- A graph is a tree if and only if it is minimally connected.
- Any connected graph with n vertices and (n-1) edges is a tree.
To gain better understanding about Tree Data Structure,
Tree Terminology-
The important terms related to tree data structure are-
1. Root-
- The first node from where the tree originates is called as a root node.
- In any tree, there must be only one root node.
- We can never have multiple root nodes in a tree data structure.
Example-
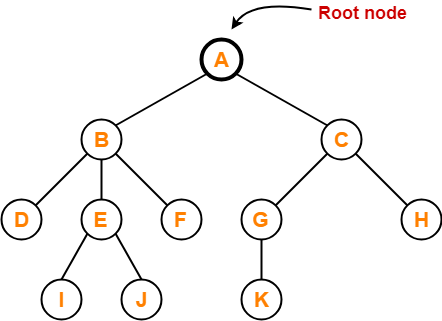
Here, node A is the only root node.
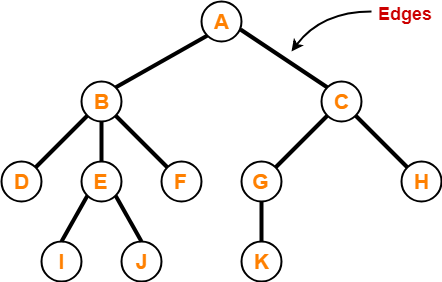
2. Edge-
- The connecting link between any two nodes is called as an edge.
- In a tree with n number of nodes, there are exactly (n-1) number of edges.
Example-
3. Parent-
- The node which has a branch from it to any other node is called as a parent node.
- In other words, the node which has one or more children is called as a parent node.
- In a tree, a parent node can have any number of child nodes.
Example-
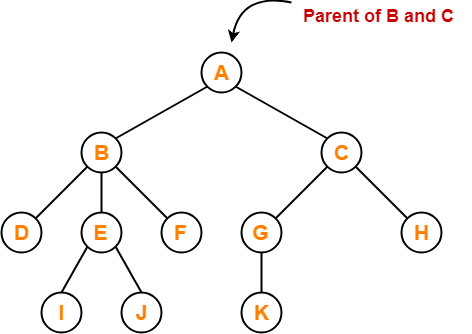
Here,
- Node A is the parent of nodes B and C
- Node B is the parent of nodes D, E and F
- Node C is the parent of nodes G and H
- Node E is the parent of nodes I and J
- Node G is the parent of node K
4. Child-
- The node which is a descendant of some node is called as a child node.
- All the nodes except root node are child nodes.
Example-
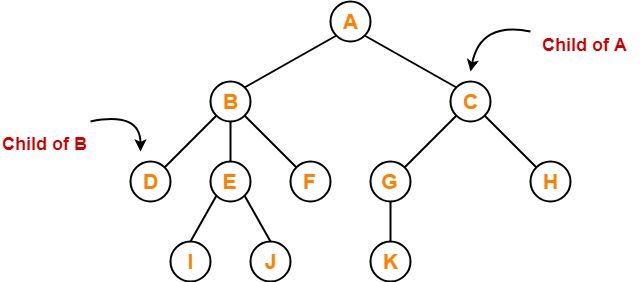
Here,
- Nodes B and C are the children of node A
- Nodes D, E and F are the children of node B
- Nodes G and H are the children of node C
- Nodes I and J are the children of node E
- Node K is the child of node G
5. Siblings-
- Nodes which belong to the same parent are called as siblings.
- In other words, nodes with the same parent are sibling nodes.
Example-
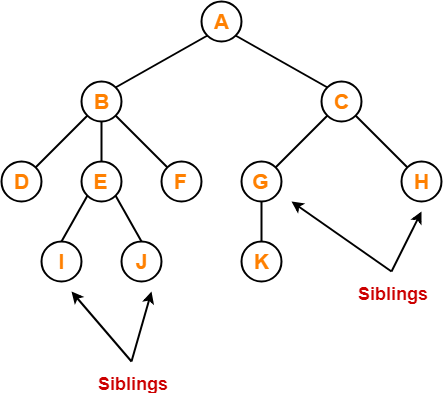
Here,
- Nodes B and C are siblings
- Nodes D, E and F are siblings
- Nodes G and H are siblings
- Nodes I and J are siblings
6. Degree-
- Degree of a node is the total number of children of that node.
- Degree of a tree is the highest degree of a node among all the nodes in the tree.
Example-
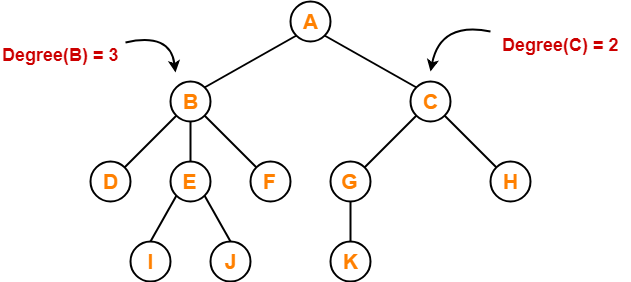
Here,
- Degree of node A = 2
- Degree of node B = 3
- Degree of node C = 2
- Degree of node D = 0
- Degree of node E = 2
- Degree of node F = 0
- Degree of node G = 1
- Degree of node H = 0
- Degree of node I = 0
- Degree of node J = 0
- Degree of node K = 0
7. Internal Node-
- The node which has at least one child is called as an internal node.
- Internal nodes are also called as non-terminal nodes.
- Every non-leaf node is an internal node.
Example-

Here, nodes A, B, C, E and G are internal nodes.
8. Leaf Node-
- The node which does not have any child is called as a leaf node.
- Leaf nodes are also called as external nodes or terminal nodes.
Example-
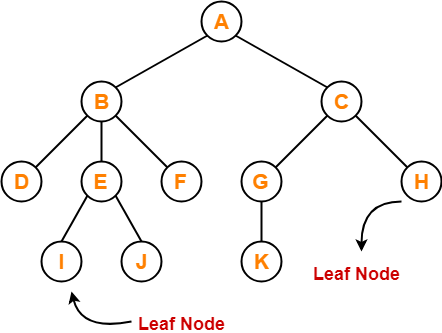
Here, nodes D, I, J, F, K and H are leaf nodes.
9. Level-
- In a tree, each step from top to bottom is called as level of a tree.
- The level count starts with 0 and increments by 1 at each level or step.
Example-
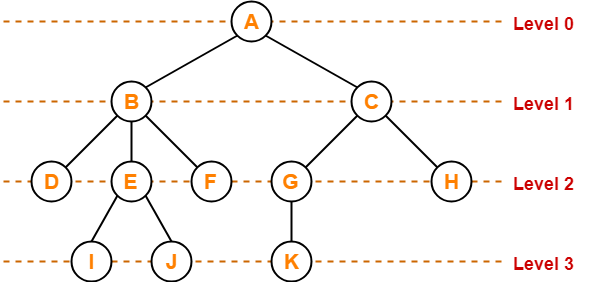
10. Height-
- Total number of edges that lies on the longest path from any leaf node to a particular node is called as height of that node.
- Height of a tree is the height of root node.
- Height of all leaf nodes = 0
Example-
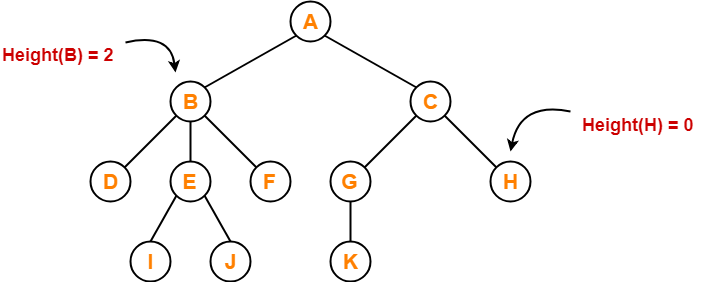
Here,
- Height of node A = 3
- Height of node B = 2
- Height of node C = 2
- Height of node D = 0
- Height of node E = 1
- Height of node F = 0
- Height of node G = 1
- Height of node H = 0
- Height of node I = 0
- Height of node J = 0
- Height of node K = 0
11. Depth-
- Total number of edges from root node to a particular node is called as depth of that node.
- Depth of a tree is the total number of edges from root node to a leaf node in the longest path.
- Depth of the root node = 0
- The terms “level” and “depth” are used interchangeably.
Example-
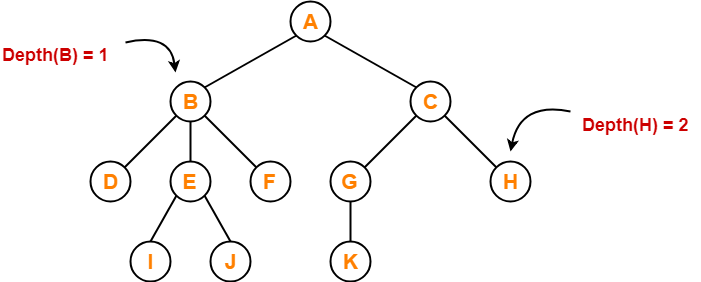
Here,
- Depth of node A = 0
- Depth of node B = 1
- Depth of node C = 1
- Depth of node D = 2
- Depth of node E = 2
- Depth of node F = 2
- Depth of node G = 2
- Depth of node H = 2
- Depth of node I = 3
- Depth of node J = 3
- Depth of node K = 3
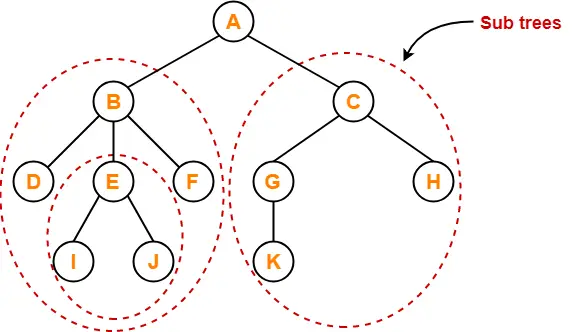
12. Subtree-
- In a tree, each child from a node forms a subtree recursively.
- Every child node forms a subtree on its parent node.
Example-
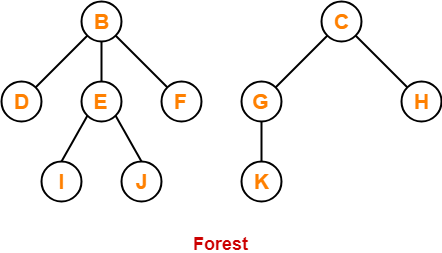
13. Forest-
A forest is a set of disjoint trees.
Example-
To gain better understanding about Tree Terminology,
Download Handwritten Notes Here-
Next Article- Binary Tree | Types of Binary Trees
Get more notes and other study material of Data Structures.
Watch video lectures by visiting our YouTube channel LearnVidFun.


