Dijkstra Algorithm-
- Dijkstra Algorithm is a very famous greedy algorithm.
- It is used for solving the single source shortest path problem.
- It computes the shortest path from one particular source node to all other remaining nodes of the graph.
Also Read- Shortest Path Problem
Conditions-
It is important to note the following points regarding Dijkstra Algorithm-
- Dijkstra algorithm works only for connected graphs.
- Dijkstra algorithm works only for those graphs that do not contain any negative weight edge.
- The actual Dijkstra algorithm does not output the shortest paths.
- It only provides the value or cost of the shortest paths.
- By making minor modifications in the actual algorithm, the shortest paths can be easily obtained.
- Dijkstra algorithm works for directed as well as undirected graphs.
Dijkstra Algorithm-
dist[S] ← 0 // The distance to source vertex is set to 0
Π[S] ← NIL // The predecessor of source vertex is set as NIL
for all v ∈ V - {S} // For all other vertices
do dist[v] ← ∞ // All other distances are set to ∞
Π[v] ← NIL // The predecessor of all other vertices is set as NIL
S ← ∅ // The set of vertices that have been visited 'S' is initially empty
Q ← V // The queue 'Q' initially contains all the vertices
while Q ≠ ∅ // While loop executes till the queue is not empty
do u ← mindistance (Q, dist) // A vertex from Q with the least distance is selected
S ← S ∪ {u} // Vertex 'u' is added to 'S' list of vertices that have been visited
for all v ∈ neighbors[u] // For all the neighboring vertices of vertex 'u'
do if dist[v] > dist[u] + w(u,v) // if any new shortest path is discovered
then dist[v] ← dist[u] + w(u,v) // The new value of the shortest path is selected
return dist
Implementation-
The implementation of above Dijkstra Algorithm is explained in the following steps-
Step-01:
In the first step. two sets are defined-
- One set contains all those vertices which have been included in the shortest path tree.
- In the beginning, this set is empty.
- Other set contains all those vertices which are still left to be included in the shortest path tree.
- In the beginning, this set contains all the vertices of the given graph.
Step-02:
For each vertex of the given graph, two variables are defined as-
- Π[v] which denotes the predecessor of vertex ‘v’
- d[v] which denotes the shortest path estimate of vertex ‘v’ from the source vertex.
Initially, the value of these variables is set as-
- The value of variable ‘Π’ for each vertex is set to NIL i.e. Π[v] = NIL
- The value of variable ‘d’ for source vertex is set to 0 i.e. d[S] = 0
- The value of variable ‘d’ for remaining vertices is set to ∞ i.e. d[v] = ∞
Step-03:
The following procedure is repeated until all the vertices of the graph are processed-
- Among unprocessed vertices, a vertex with minimum value of variable ‘d’ is chosen.
- Its outgoing edges are relaxed.
- After relaxing the edges for that vertex, the sets created in step-01 are updated.
What is Edge Relaxation?
Consider the edge (a,b) in the following graph-
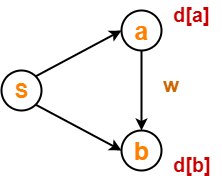
Here, d[a] and d[b] denotes the shortest path estimate for vertices a and b respectively from the source vertex ‘S’.
Now,
If d[a] + w < d[b]
then d[b] = d[a] + w and Π[b] = a
This is called as edge relaxation.
Time Complexity Analysis-
Case-01:
This case is valid when-
- The given graph G is represented as an adjacency matrix.
- Priority queue Q is represented as an unordered list.
Here,
- A[i,j] stores the information about edge (i,j).
- Time taken for selecting i with the smallest dist is O(V).
- For each neighbor of i, time taken for updating dist[j] is O(1) and there will be maximum V neighbors.
- Time taken for each iteration of the loop is O(V) and one vertex is deleted from Q.
- Thus, total time complexity becomes O(V2).
Case-02:
This case is valid when-
- The given graph G is represented as an adjacency list.
- Priority queue Q is represented as a binary heap.
Here,
- With adjacency list representation, all vertices of the graph can be traversed using BFS in O(V+E) time.
- In min heap, operations like extract-min and decrease-key value takes O(logV) time.
- So, overall time complexity becomes O(E+V) x O(logV) which is O((E + V) x logV) = O(ElogV)
- This time complexity can be reduced to O(E+VlogV) using Fibonacci heap.
PRACTICE PROBLEM BASED ON DIJKSTRA ALGORITHM-
Problem-
Using Dijkstra’s Algorithm, find the shortest distance from source vertex ‘S’ to remaining vertices in the following graph-
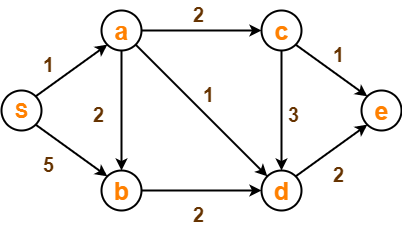
Also, write the order in which the vertices are visited.
Solution-
Step-01:
The following two sets are created-
- Unvisited set : {S , a , b , c , d , e}
- Visited set : { }
Step-02:
The two variables Π and d are created for each vertex and initialized as-
- Π[S] = Π[a] = Π[b] = Π[c] = Π[d] = Π[e] = NIL
- d[S] = 0
- d[a] = d[b] = d[c] = d[d] = d[e] = ∞
Step-03:
- Vertex ‘S’ is chosen.
- This is because shortest path estimate for vertex ‘S’ is least.
- The outgoing edges of vertex ‘S’ are relaxed.
Before Edge Relaxation-
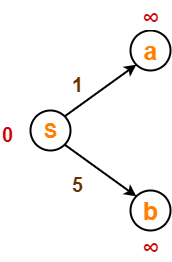
Now,
- d[S] + 1 = 0 + 1 = 1 < ∞
∴ d[a] = 1 and Π[a] = S
- d[S] + 5 = 0 + 5 = 5 < ∞
∴ d[b] = 5 and Π[b] = S
After edge relaxation, our shortest path tree is-
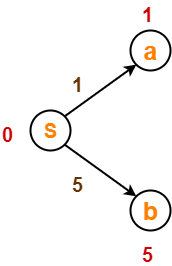
Now, the sets are updated as-
- Unvisited set : {a , b , c , d , e}
- Visited set : {S}
Step-04:
- Vertex ‘a’ is chosen.
- This is because shortest path estimate for vertex ‘a’ is least.
- The outgoing edges of vertex ‘a’ are relaxed.
Before Edge Relaxation-
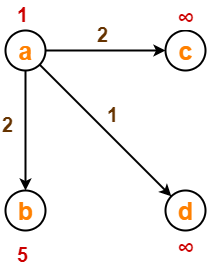
Now,
- d[a] + 2 = 1 + 2 = 3 < ∞
∴ d[c] = 3 and Π[c] = a
- d[a] + 1 = 1 + 1 = 2 < ∞
∴ d[d] = 2 and Π[d] = a
- d[b] + 2 = 1 + 2 = 3 < 5
∴ d[b] = 3 and Π[b] = a
After edge relaxation, our shortest path tree is-
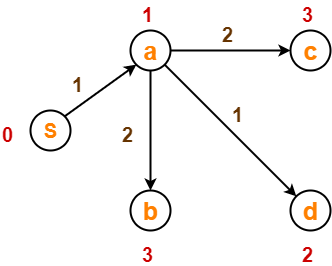
Now, the sets are updated as-
- Unvisited set : {b , c , d , e}
- Visited set : {S , a}
Step-05:
- Vertex ‘d’ is chosen.
- This is because shortest path estimate for vertex ‘d’ is least.
- The outgoing edges of vertex ‘d’ are relaxed.
Before Edge Relaxation-
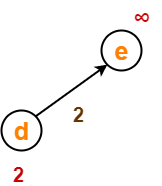
Now,
- d[d] + 2 = 2 + 2 = 4 < ∞
∴ d[e] = 4 and Π[e] = d
After edge relaxation, our shortest path tree is-
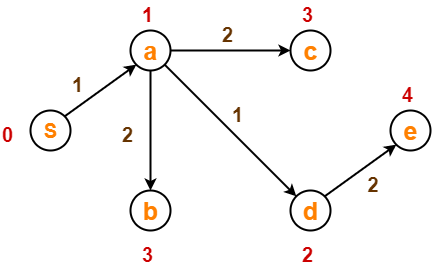
Now, the sets are updated as-
- Unvisited set : {b , c , e}
- Visited set : {S , a , d}
Step-06:
- Vertex ‘b’ is chosen.
- This is because shortest path estimate for vertex ‘b’ is least.
- Vertex ‘c’ may also be chosen since for both the vertices, shortest path estimate is least.
- The outgoing edges of vertex ‘b’ are relaxed.
Before Edge Relaxation-
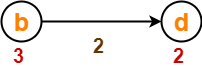
Now,
- d[b] + 2 = 3 + 2 = 5 > 2
∴ No change
After edge relaxation, our shortest path tree remains the same as in Step-05.
Now, the sets are updated as-
- Unvisited set : {c , e}
- Visited set : {S , a , d , b}
Step-07:
- Vertex ‘c’ is chosen.
- This is because shortest path estimate for vertex ‘c’ is least.
- The outgoing edges of vertex ‘c’ are relaxed.
Before Edge Relaxation-
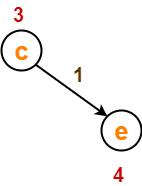
Now,
- d[c] + 1 = 3 + 1 = 4 = 4
∴ No change
After edge relaxation, our shortest path tree remains the same as in Step-05.
Now, the sets are updated as-
- Unvisited set : {e}
- Visited set : {S , a , d , b , c}
Step-08:
- Vertex ‘e’ is chosen.
- This is because shortest path estimate for vertex ‘e’ is least.
- The outgoing edges of vertex ‘e’ are relaxed.
- There are no outgoing edges for vertex ‘e’.
- So, our shortest path tree remains the same as in Step-05.
Now, the sets are updated as-
- Unvisited set : { }
- Visited set : {S , a , d , b , c , e}
Now,
- All vertices of the graph are processed.
- Our final shortest path tree is as shown below.
- It represents the shortest path from source vertex ‘S’ to all other remaining vertices.
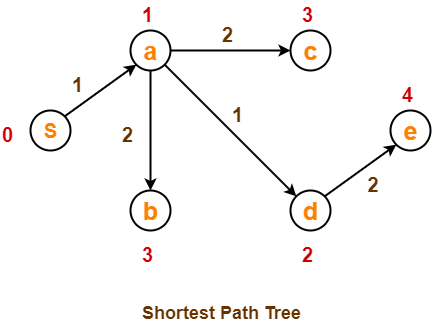
The order in which all the vertices are processed is :
S , a , d , b , c , e.
To gain better understanding about Dijkstra Algorithm,
Next Article- Floyd-Warshall Algorithm
Get more notes and other study material of Design and Analysis of Algorithms.
Watch video lectures by visiting our YouTube channel LearnVidFun.